大规模高阶张量与向量相乘的一种并行算法
2021-11-01张正东
张正东
(贵阳学院数学与信息科学学院,贵阳 550005)
0 引言
随着大数据和人工智能技术的快速发展,其应用范围越来越广,产生和汇集了海量数据,数据属性越来越多,维度越来越大,如何表示和处理海量高维数据以挖掘数据价值是我们面临的一大挑战[1]。张量因其多维特性是解决这一问题的有效方法。张量在数学上是多维数组或多维阵列,可用多个下标表示,是向量和矩阵概念向高维空间的推广。张量的维数称为阶(order)或模(mode)[2],高阶张量具有多个维度,非常适合用来表示现实世界中的多维、复杂数据,如复杂网络、多维社交关系等。张量在人工智能中得到了广泛应用,现在流行的深度学习框架TensorFlow就将张量作为一种基本数据模型[3]。高阶张量随着维度的增加,表示的多维关系越来越复杂,存储的数据量也越来越大,如5阶张量,每阶数据量为1 000,总数据量为103*103*103*103*103=1015,如此海量数据对存储和计算提出了更高要求。实际应用中,高阶张量往往是稀疏的,也即只有一部分元素是非0值。在此情况下,我们需要设计一种有效的存储方案以扩大张量的应用范围,并能以并行计算或分布式计算方式进行数据处理。
并行计算是处理海量数据的常用方法之一。随着CPU和GPU技术的发展,其核心数越来越多,特别是在GPU计算中,可以开启几十、几百上甚至千个线程并行处理数据[4],能大大降低计算时间。采用并行方式处理数据,数据在本地完成处理,可避免数据在集群中传播、计算任务分发和结果收集的时间开销,同时也能更好的发挥机器算力。在集群环境中,计算节点上开启多线程进行并行计算能更好的提高数据处理效率[5],这也是很多流行的分布式计算框架采用的方法,比如分布式内存计算框架Spark。
张量的一种基本运算是与向量相乘,以此达到对张量降维的目的,是最频繁的张量运算之一,该步骤的计算速度对整体性能有较大影响。本文的研究内容即是如何用key-value对表示高阶张量并实现张量与向量的并行相乘。
1 算法实现
1.1 算法描述
对于N维空间张量X∈RI1×I2×…×I N和1维空间向量v∈RI n,张量和向量的mode-n相乘规则为公式(1)。mode-n是指向量和张量的哪个维度相乘。

从公式(1)可以看出,张量与向量相乘的结果也是张量,但已经没有n维度了,即消去了n维度,结果张量少了一个维度,对张量进行了降维。张量和向量mode-n相乘的过程是固定张量其他维度下标,遍历n维度下标,用此下标到向量中取值并和张量元素值相乘,最后将下标相同的元素求和。这就要求张量n维度的元素个数和向量元素个数相同。如张量X∈R2×2×2和向量v∈R2的mode-2相乘,结果为张量X'∈R2×2,如公式(2)所示。其中,张量和向量元素值用下标表示。
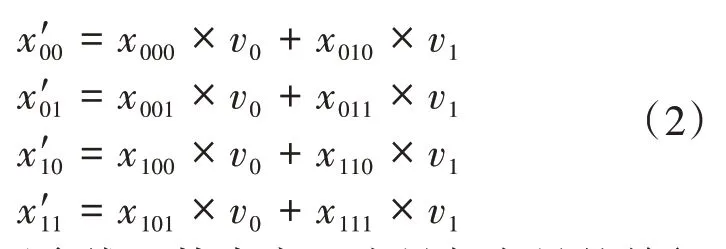
为了采用多线程技术实现张量与向量的并行相乘,我们可以用key-value对表示张量元素,其中key为张量元素下标组合,value为元素值。这样张量就可以转换成Map或者列表(列表元素是自定义的JavaBean,包含key和value属性)。通过将Map或者列表均匀分割,开启多线程,每个线程处理一部分,最后汇聚,从而实现张量和向量并行相乘。公式(1)表明,采用分割-汇聚策略,对最终结果没有影响。我们只对张量中非0值元素进行转换,对于0值元素,根据公式(1),其和向量元素相乘结果也为0,对求和结果没有影响。张量与向量并行相乘过程如算法1。算法1采用了线程池技术对线程进行管理和复用,避免多次创建线程开销,并在每个线程中进行局部汇聚,实现局部优化,进而提高计算效率。
算法1张量与向量并行相乘。
1.定义包含key和value属性的JavaBean,表示张量非0值元素。
2.将张量转换为列表。
3.将列表均匀分割,启动线程池,每部分用一个线程计算。
4.对于每一个计算线程,遍历列表元素:
5. 对于每一个key-value对,将key分割成张量下标。
6. 用n维度下标到向量中取值并和value相乘,得到新值value'。
7.去除n维度下标,重新生成key'。
8.将key'-value'放到Map中,进行局部汇聚。
9.收集线程计算结果,进行全局汇聚。
10.生成结果。
1.2 实现代码
算法1程序实现主要包括两部分,一是均匀分割张量元素列表,每部分对应一个计算线程,通过线程池管理;二是在每个线程内部实现张量和向量相乘。第一部分实现程序为:
private Map<String,Integer>computeInThread(List<Element>dataList,int threadCount,final int[]vector,final int modeN){
int cpuCore=Runtime.get Runtime().availableProcessors();//获取CPU核心数
//计算线程池最大容量
int pool Size=threadCount<=cpuCore?thread-Count:cpuCore;
int threadSize=dataList.size()/threadCount;//每个线程处理数据量
//创建固定大小的线程池
ExecutorService executorService = Executors.new-FixedThreadPool(poolSize);
for(int index=0;index<threadCount;index++){
//根据线程数量,计算每部分开始和结束下标
int fromIndex=index*threadSize;
int toIndex=(index+1)*threadSize;
if(index==threadCount-1){
toIndex=dataList.size();
}
if(fromIndex<toIndex){
//通过下标取列表部分,分割列表
final List<Element>tensor=dataList.subList(fromIndex,toIndex);
//以lambda表达式形式向线程池提交一个计算线程任务
executorService.execute(()->ttv(tensor,vector,modeN));
}
}
executorService.shutdown();//关闭线程池,等待计算完成
while(true){
if(executorService.isTerminated()){
break;
}
}
//全局结果
Map<String,Integer>result Map=new HashMap<>();
//tmpResultList是全局列表,存放了每个线程计算结果
for(Map<String,Integer> tmpResult Map:tmpResultList){
for(String key:tmpResultMap.keySet()){
int tmpValue=tmpResultMap.get(key);
//全局汇聚
processMapElement(resultMap,key,tmpValue);
}
}
return result Map;
}
上述程序中的processMapElement函数进行Map中元素汇聚,将相同key的元素值求和,程序代码为:
private void processMapElement(Map<String,Integer>map,String key,int value){
int rValue=value;
if(map.containsKey(key)){
//若key已经存在,将值求和
rValue+=map.get(key);
}
map.put(key,rValue);
}
ttv函数为张量和向量相乘,也即第二部分,程序代码为:
private void ttv(List<Element>tensor,int[]vector,int modeN){
Map<String,Integer>resultMap=new HashMap<>();
//局部结果map
for(Element element:tensor){//遍历张量元素
String[]keySplits=element.getKey().split("#");
//分割key
int value=element.getValue();
//到向量中取值并和张量值相乘
int mValue=value*vector[Integer.parseInt(key-Splits[modeN-1])];
String mKey="";
//去除相乘维度下标,组合新的key
for(int index=0;index<keySplits.length;index++){
if(index!=modeN-1){
mKey=mKey+keySplits[index]+"#";
}
}
//去除结尾的分隔符
if(mKey.endsWith("#")){
mKey=mKey.substring(0,mKey.length()-1);
}
//局部汇聚
processMapElement(result Map,mKey,mValue);
}
tmpResultList.add(resultMap);
}
ttv函数中,我们定义了一个全局列表,用于收集每个线程的计算结果。由于多个线程都会向全局列表中添加数据,为了避免数据混乱,我们采用了具有线程写安全性的CopyOnWriteArray List。我们将张量与向量乘积结果放在Map中,其中key为张量元素下标组合,value为值。结果Map可以很容易转换为元素列表,或者将key拆分还原到张量中,以进行下一步处理。
2 结果与分析
算法采用了Java实现,JDK版本为8u181,机器内存为16 G,CPU为Intel i7-7700HQ,核心数为8。我们进行了两次运算,一次是低阶张量和向量相乘,用于测试算法的准确性,张量X∈R2×2×2和向量v∈R2,元素值随机产生,进行mode-2相乘,结果如图1所示。

图1 张量和向量mode-2相乘的结果
其中,冒号(:)表示所有下标,x是原张量,v是向量,x'是结果张量。
另一次运算是测试计算规模和时间,我们分别设置计算线程数为6、10和16,线程池容量为线程数和机器核心数的最小值,非0元素下标和值以及向量值均随机产生,对于每个线程数计算三次,取平均时间,计算结果如表1所示。数据表明,我们实现的并行算法可用于大规模张量与向量相乘,随着线程数的增加,计算的并行度提高,计算时间也进一步降低。实际应用中可根据机器配置,设置合适的线程数量。因为算法1只对张量中的非0值进行处理,对于稀疏张量,由于大部分是0值,算法的性能会更高,能处理的数据规模也更大。

表1 大规模高阶稀疏张量与向量相乘数据
