Hermitian unital中的两个无限2-设计族
2022-07-02李荣荣詹小秦
李荣荣,詹小秦
(华东交通大学理学院, 江西 南昌 330013)
0 引言
2-(v,k,λ)设计D是一个关联结构(P,E),其中P是v个元素的点集,E是b个P中的k-元子集构成的区组集合,满足任意两个不同的点恰好与λ个区组关联(此时的关联关系为包含关系).设r为与给定点关联的区组数.若b=v(或由引理1.1等价地有r=k),则称设计D为对称设计.否则,称之为非对称设计.n阶unital是一个2-(n3+1,n+1,1)设计.当n=q(素数幂)时,此设计就是Hermitian unital,记为UH(q).正整数v,b,r,k,λ称为设计的参数.若设计的参数满足2 D的一个自同构是P上的一个置换,并诱导出E的置换.D的全体自同构构成了D的全自同构群,记作Aut(D),并称Aut(D)的子群为D的自同构群.取G≤Aut(D),如果G作用在P的点集上是本原的,则称设计D=(P,E)为点本原的,如果G在设计D的旗(或区组)上传递,则称设计D是旗(区)传递的,其中D的旗为任意一个点区对(α,B)且α∈B. 设计理论的一个主要问题是对给定参数或给定自同构群的设计进行结构分类.1985年, Kantor[1]使用有限2-传递置换群的分类确定了所有的(G,S),其中G是作用在线性空间S(2-(v,k,1)设计)上的一个2-传递群.注意,此时G是区传递的.这一结果被Delandsheer等[2]推广到了G2-齐次作用在S的点集上的情形. F.Buekenhout等[3]在1990年对旗传递线性空间进行了分类,结果如下. 定理0.1[3]设D=(P,E)是一个2-(v,k,1)设计,且G≤Aut(D)旗传递作用在D上.则下列情形之一成立: a.若G是2-齐次但非2-传递的,则v=pn,p≡3 (mod 4),其中p是素数,n是奇数.则下列情形之一成立: 1)D是GF(pn)子域上的仿射空间; 2)D是Netto系,k=3,pn≡7 (mod 12). b. 若G是2-传递的,则下列情形之一成立: 1)D=PG(d,q)是GF(q)上的d-维射影空间,且PSL(d+1,q)≤G≤PΓL(d+1,q),或(d,q)=(3,2)且G=A7; 2)D=AG(d,q)是GF(q)上的仿射空间,d≥2且G是AΓL(d+1,q)的2-传递子群; 3)D是Hermitian unital; 4)D是Ree unital; 5)D是两个非Desargusian仿射平面,k=27或k=9; c.D是Witt-Bose-Shrikhande空间; d.D是非Desarguesian Luneburg仿射平面,其阶数为k=22e+1; e.G≤AΓL(1,v),v为素数幂. 另一方面,对λ>1的旗传递2-设计似乎很难实现其完全分类.目前为止,也仅得到了部分结果.如,Regueiro[4-7]给出了除一维仿射群外的旗传递和点本原双平面(λ=2的对称设计)的分类. 定理0.2[4-7]如果D=(P,E)是具有旗传递点本原自同构群G的非平凡双平面,则下列情形之一成立: a.D是2-(16,6,2)设计; b.D是2-(7,4,2)设计; c.D是2-(11,5,2)设计; d.G≤AΓL(1,q),q是奇素数幂. 以下为董会莉[8]对旗传递三平面(λ=3的对称设计)的分类结果. 定理0.3[8]如果D=(P,E)是具有旗传递点本原自同构群G的非平凡三平面,则下列情形之一成立: a.D是2-(45,12,3)设计; b.D是2-(11,6,3)设计; c.D是2-(15,7,3)设计; d.G≤AΓL(1,q),其中q(q≥5)是素数p的方幂. 此外,Alavi在文献[9-10]中研究了对称设计在其他类型下的分类,并在文献[11]中得到如下结果: 定理0.4[11]设D是满足gcd(r,λ)=1的非平凡2-设计,假设G是D上的旗传递群,其中D的基柱为PSU(n,q)且(n,q)≠(3,2).那么n=2或者n=3. a.若n=2,则此时D是一个Witt-Bose-Shrikhande空间,或者D是一个有参数的设计(v,k,λ)=(6,3,2),(7,3,1),(8,4,3),(10,6,5),(11,5,2),(28,7,2); b.若n=3,则D是一个Hermitian unital,即2-(q3+1,q+1,1)设计. 2021年Zhan-Ding[12]发现了以上结论忽略了当λ>1时的情形,并给出了新的证明,得到结果如下: 定理0.5[12]设D是一个非平凡的2-(q3+1,k,λ)设计,且gcd(r,λ)=1.假设G是D的旗传递群,其中D的基柱是X=PSU(3,q),q>2.如果λ>1,则D是一个2-(q3+1,q,q-1)设计. 如果D是一个满足gcd(r,λ)=1的2-(v,k,λ)设计,由Dembowski[13]的结论知,此时任意D上的旗传递自同构群G是点本原的,并且在1988年,Zieschang[14]证明了此时G的基柱T是下列情形之一: a)T是初等交换群; b)T是非交换单群. Biliotti[15]处理了a)的情况,但并没有给出非对称的情形.对于b)的情况,王亚杰[16]和Zhu-Guan-Zhou[17]给出了T是交替群An(n≥5)时的分类结果.另外,Zhan-Zhou[18]还研究了T是散在单群和二维特殊射影线性群时的分类结果.Alavi还研究了例外李型单群[19]的情形以及其他情况[20]下的分类. 以上研究结果表明,对旗传递2-设计的分类还远远没有结束.本研究的主要目的是构造Hermitian unital中两个以PSU(3,q)作为旗传递自同构群的无限2-设计族,对旗传递2-设计分类的研究具有很重要的参考意义. 本节给出后续要用到的关于设计理论和群论的一些重要结果. 引理1.1[13,p57,2.1.5]2-设计D的参数v,b,r,k,λ满足以下条件: 1)vr=bk; 2)λ(v-1)=r(k-1). 设G作用在P上是2-齐次的.选择P的子集B,并定义一个关联结构(P,E),其中E={Bg|g∈G},对任意的α∈P,g∈G有α与Bg关联,当且仅当α∈Bg.设D=(P,E),则下列引理成立. 引理1.2[13,p93]关联结构D是一个区传递2-设计,其参数为 v=|P|,k=|B|,b=[G:GB], 且r,λ由引理1.1确定. 引理1.3[13,1.2(16)]设G是2-设计D=(P,E)的一个自同构群.则G旗传递作用于D当且仅当G是区传递的且对任意的B∈E,群GB在B的点集上传递. 本文中接下来的部分均假设G=PSU(3,q)(q>2)为三维特殊射影酉群,UH(q)是一个Hermitian unital,且P是UH(q)的点集.因此|P|=q3+1. 群G2-传递作用在P上,如果α,β是P中任两个不同的点,则这两点的稳定子群Gαβ有唯一一个长为q-1的轨道Δ.设B=Δ∪{β},L=Δ∪{α,β},显然,L是UH(q)中过点α和β的区组. 2.1 旗传递2-(q3+1,q,q-1)设计 命题2.1区稳定子群GL在区组L的点集上是2-传递的,且有GαL=GB. 命题2.1的证明显然,GαL≤GB.由于UH(q)中存在唯一的区组经过两个给定点,而B⊂L,且|B|≥3从而有GB≤GL,又因为任取g∈GB,有Bg=B,而αg=(L-B)g=Lg-Bg=L-B=α.故有GB≤Gα∩GL=GαL,从而GαL=GB.显然,由Gαβ 定理2.1设E1=BG,则关联结构D1=(P,E1)是一个2-(q3+1,q,q-1)设计,且G为D1的旗传递自同构群. 故D1是一个2-(q3+1,q,q-1)设计.命题2.1说明GL在L的点集上是2-传递的,因此GB=GαL在B=L{α}的点集上是传递的,故由引理1.3知G是D1上的旗传递自同构群. 此结果与文献[12]中的结果是一致的,但两者之间在研究方法上是完全不同的,而且研究目标也不一样. 设G{α,β}表示G中点集{α,β}的集型稳定子群.则我们有如下结果. 命题2.2GΔ=G{α,β}. 接下来,证明G{α,β}≤GΔ.由于L是UH(q)的一个区组,Δ⊂L得出GΔ≤GL.任取g∈GΔ, {α,β}g=(L-Δ)g=Lg-Δg=L-Δ={α,β}, 即g∈G{α,β},GΔ≤G{α,β}. 综上可得GΔ=G{α,β}. 本研究从有限单群的结构出发,证明了Hermitian unital 中以3维特殊射影酉群PSU(3,q)作为旗传递自同构群的两个无限2-设计族的存在性,即下列两个设计: 1)2-(q3+1,q,q-1)设计; 本研究为旗传递2-设计提供了一种新的分类方法, 因此具有较大的参考意义.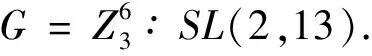
1 符号及引理
2 UH(q)中的两个2-设计族

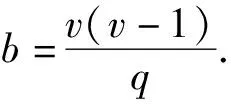

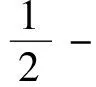
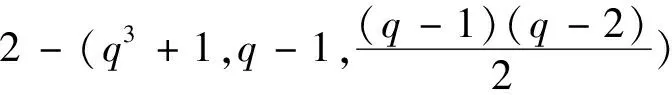

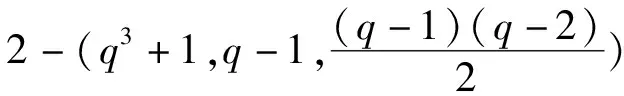
3 结论

