中立型随机泛函微分方程的p阶矩指数稳定性

余国胜

(江汉大学人工智能学院， 湖北 武汉 430056)

0 引言

众所周知，时滞在系统中无处不在.时滞既存在于系统的状态变量中，又存在于系统状态的导数项中，这样的系统称为中立型系统.Hale和Lunel[1]研究了确定性中立型泛函微分方程及其稳定性.考虑随机环境干扰，例如在生物系统，物理系统，信息科学中，因为中立型随机泛函微分方程能更精确地描述这些现象，因而中立型随机泛函微分方程越来越受到人们的关注.毛学荣[2]和胡适耕[3]研究了中立型随机泛函微分方程及其稳定性.毛学荣[4]运用Lyapunov-Razumikhin方法得到中立型随机泛函微分方程的指数稳定性.利用一对延迟积分不等式和随机分析的技巧，陈华斌等[5]探究了变时滞中立型随机线性系统的指数稳定性准则.通过运用不动点定理，罗交晚[6]考虑了变时滞一类线性标量中立型随机微分方程的渐近稳定性.庄刘和龙述君[7]运用伊藤公式、Fatou引理、局部鞅收敛定理和不等式分析诸多技巧，研究了中立型随机泛函微分方程的p阶矩稳定性和几乎必然稳定性的充分条件.张彩琴和刘桂荣[8]利Lyapunov函数方法获得了一类非线性多时滞中立型随机微分方程的p阶矩指数稳定性的若干判别准则，运用Chebyshev不等式和Borel-Cantelli引理证实了该方程的几乎必然指数稳定性.受上述文献的启发，为了克服中立项，随机干扰和变时滞同时存在所带来的困难，本文中研究中立型随机泛函微分方程的p阶矩指数稳定性，运用Lyapunov函数,推广的伊藤公式和Gronwall不等式，得到中立型随机泛函微分方程的p阶矩指数稳定性新的结果，其结论更具一般性.

1 预备知识

考虑下面的中立型泛函微分方程

d[x(t)-G(xt)]=f(xt,t)dt+g(xt,t)dB(t)

(1)

(2)

为了保证解的存在唯一性，需要以下两个假设：

|f(φ,t)-f(ψ,t)|∨|g(φ,t)-g(ψ,t)|≤L‖φ-ψ‖,

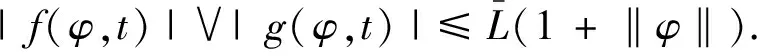
G(φ)-G(ψ)|≤κ‖φ-ψ‖,

并且G(0)=0.

2 主要结果

类似文献[9]中定理2.4的证明可得以下引理：

其中C1,C2是两个大于1的适当的正常数.

引理2.3(Gronwall不等式) 设φ(·)是R上的有界非负Borel可测函数，k(·)与β(·)是R上的非负可积函数，则

定理2.1假设H1)和H2)成立，c1,c2,λ1和λ2是4个正常数，且c1≤c2，λ1>λ2.假设存在一个函数V(x,t)∈C2,1(Rn×R+;R+)满足

1)对于所有(x,t)∈Rn×R+,

c1|x|p≤V(x,t)≤c2|x|p;

(3)

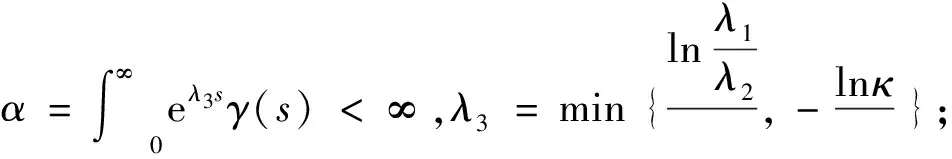
E|x(t)|p≤Me-γt,t≥0,

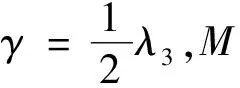
定理2.1的证明对于任意正整数N,定义停时

eλ3TNEV(x(TN)-G(xTN),TN)=EV(x(0)-G(x0),0)+

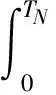
令N→∞可得

eλ3tEV(x(t)-G(xt),t)=EV(x(0)-G(x0),0)+

(4)

由(3)式有

(5)

联立(4)和(5)式可得

其中EV(x(0)-G(x0),0)≤2p-1(1+κp)E‖ξ‖p,于是

(6)

由引理2.3(Gronwall不等式)可得

(7)

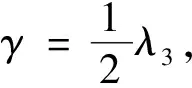
(8)

由(7)、(8)式有

E|x(t)-G(xt)|p≤M1e-γt,∀t≥0,

其中M1≥E‖ξ‖p.令

h1(t)=eγtE|x(t)|p,t≥0;h2(t)=eγtE|x(t)-G(xt)|p,t≥0.

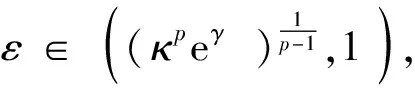
+ε1-pE‖G(xt)‖p]

+ε1-pκpeγsE‖G(xt)‖p]

故有

从而

E|x(t)|p≤Me-γt,

3 一个实例

本节通过一个具体地实例验证上一节主要定理的有效性.考虑二维中立型随机泛函微分方程：

取V(x,t)=2|x|2,

+2trace[gT(xt,t)g(xt,t)

≤-3.8|x(t)|2+1.53|x(t-0.5)|2+0.72|x(t-1)|2