WOD样本下VaR核估计的强相合性及Bahadur表示
2022-07-02王巍朱勇吴青青吴燚
王巍,朱勇,吴青青,吴燚
(池州学院大数据与人工智能学院,安徽 池州 247000)
0 引言

vp=inf{u:F(u)≥p},
其衡量了某段持有期资产价值损失的单边临界值.
VaR的早期估计主要是基于回报分布的参数估计,例如高斯分布或t分布,参数化模型在解释上具有优势,但实践中分布往往是未知的,导致计算VaR时常因模型设定错误而出错.近年来,一些学者提出了VaR的非参数估计量,非参数估计量不再受分布约束且能够自动求解收益的厚尾分布,也弱化了回报过程的动态性假定. Dowd[1]研究了基于样本分位数的VaR非参数估计,通过模拟发现,样本量越大,VaR估计精度越高. Berkowitz-Brien[2]和Inui-Kijima -Kitano[3]研究发现当投资组合具有厚尾分布特征时,基于样本分位数的VaR非参数估计具有较大的正偏差. Chen-Tang[4]提出了基于核分位数估计的VaR非参数估计,对相依条件下的金融回报率序列进行了分析. 此外,一些学者对α-混合、NA、NOD等序列样本的VaR非参数估计进行了研究[5-12].
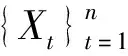
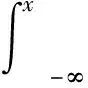
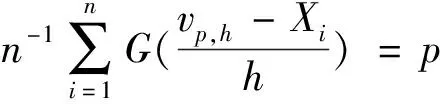
WOD随机变量序列的概念是由Wang-Wang-Gao[14]2013年提出的. WOD是一类更具有普遍性、更弱的相依结构.
定义1[14]称{Xn,n≥1}为上宽象限相依随机变量序列(WUOD),若存在有限的实数序列{gU(n),n≥1},使得对每个n≥1,xi∈(-∞,+∞),1≤i≤n都有
(1)
称{Xn,n≥1}为下宽象限相依随机变量序列(WLOD),若存在有限的实数序列{gL(n),n≥1},使得对每个n≥1,xi∈(-∞,+∞),1≤i≤n都有
(2)
若{Xn,n≥1}既是WUOD随机变量序列,又是WLOD随机变量序列,则称{Xn,n≥1}为WOD随机变量序列,其控制系数记为g(n)=max{gU(n),gL(n)}.显然,由gU(n)≥1与gL(n)≥1可知g(n)≥1,n≥1.
之后,一些学者研究了WOD序列,取得了一些有意义的结论[15-17]. 通过调整控制系数g(n)可知,WOD结构包含了其他相依结构. 当gU(n)=gL(n)=M,M是一个正数,式(1)和(2)同时成立,则称随机变量为END的;当gU(n)=gL(n)=1,式(1)和(2)同时成立,则称随机变量为NOD的. Joag-Proschan[18]指出NA随机变量是NOD的. Hu[19]引入了NSD的概念并指出NSD包含NOD. 可见,WOD结构包含了独立随机变量序列、NA、NSD、NOD及END序列. 因此,研究WOD样本下的VaR核估计量具有重要意义.本研究利用WOD序列的性质及其指数不等式研究了VaR核估计量的性质,同时给出了VaR核估计的收敛速率和Bahadur表示,推广和改进了Chen-Tang[4]、Wei-Yang-Yu[5]以及Yang等[20]相关文献的研究结果.
1 主要结果及证明
为了获得本文中的主要结果,需要首先给出几个引理.
引理1[14]设序列{Xn,n≥1}是WLOD(WUOD)变量,如果{fn(·),n≥1}均为非降函数,则随机变量{fn(Xn),n≥1}也是WUOD(WLOD)变量;如果{fn(·),n≥1}均为非增函数,则随机变量{fn(Xn),n≥1}也是WUOD(WLOD)变量.
引理2[20]设{Xn,n≥1}是WOD随机变量,控制系数g(n)=max{gU(n),gL(n)},EXi=0,对于每个i≥1,|Xi|≤b,b为正数,对于任意0 其中,K=b2/2(1-C). 引理3[21]设F(X)为右连续的分布函数,则其反函数F-1(t)是非降且左连续的,当且仅当x≥F-1(t)时,F(x)≥t. 下面将给出本文中的主要结果及其证明. 定理1设0 A=P(|vp,h-vp|>εn) =P(vp,h>vp+εn)+P(vp,h =P(p-F(vp+εn)>Fn,h(vp+εn)-F(vp+εn)) +P(p-F(vp-εn)>Fn,h(vp-εn)-F(vp-εn)). 由F(x)在vp处连续且F′(vp)=f(vp)>0,将F(vp±εn)在vp处泰勒展开可以得到 A=P(Fn,h(vp+εn)-F(vp+εn)<-f(vp+θ1εn)εn) +P(Fn,h(vp-εn)-F(vp-εn)>f(vp-θ2εn)εn) ≤P(|Fn,h(vp+εn)-F(vp+εn)|>c1εn)+P(|Fn,h(vp-εn)-F(vp-εn)|>c1εn) 其中,θ1,θ2∈(0,1),c1=infx∈[vp-εn,vp+εn]f(x)>0,因此,当n充分大时,有 (3) P(|Fn,h(vp+εn)-F(vp+εn)|>c1εn) 其中,K1=2/(1-C). (4) 令λ=4K,由式(4)可得 由Borel-Cantelli引理可知,|vp,h-vp|≤εn以概率1成立,从而定理得证. Fn(x)-F(x)-Fn(vp)+p≤Fn(mk+1,n)-F(mk+1,n)-Fn(vp)+p≤δk+1,n+Tεn (5) 及 Fn(x)-F(x)-Fn(vp)+p≥Fn(mk,n)-F(mk,n)-Fn(vp)+p≥δk+1,n-Tεn (6) 由式(5)和(6)可得 (7) 对于任意给定k,易知 (8) (9) 其中,K1=2/(1-C2). 类似可得,当n充分大时,有 (10) 令C1=17K1,结合式(8)~(10)可得,当n充分大时, 定理3假定定理2条件成立,那么存在常数C2,使得当n充分大时,以概率1有 dk,n-Tεn≤Fn(x)-F(x)≤dk+1,n+Tεn 进一步可得 (11) P(|dk,n|>εn)=P(|Fn(vp+kεn)-F(vp+kεn)|>εn) 其中,K2=2/(1-C3). 定理4的证明首先由定理1和定理2可得 (12) 再结合定理3和Taylor定理,可以得到 |Fn(vp)-p|≤|Fn(vp,h)-F(vp,h)|+|F(vp,h)-F(vp)|≤ (13) 另外,通过泰勒展开并结合式(12)、(13)可知, 其中,ωn为一介于vp,h和vp间的随机变量. 由以上等式可得 从而定理4得证. 注1Chen-Tang[4]以及Wei -Yang -Yu[5]在α混合样本下分别研究了VaR核估计和线性核分位数估计,笔者研究WOD样本的VaR核估计,研究结果推广了Chen-Tang以及Wei-Yang -Yu的相应内容. 注2与Yang等[20]比较,本文中在研究WOD样本下VaR核估计时,获得了与Yang等相似的收敛速率,而当核函数G(x)=I(x≥0)时,结果退化成Yang等[20]的形式,可见,此结果更具有一般性. 为了进一步验证本文中所得的理论结果,下面将运用R软件进行数值模拟.模拟将分别考虑独立样本和相依样本两种情况,将VaR核估计和样本分位数估计进行对比,比较二者同实际值的绝对偏差大小.概率水平p=0.05,样本量n依次为100,200和300,实验重复500次,核函数采用高斯核.独立样本产生于标准正态分布,相依样本根据Liu[22]的例4.1得到,其中Xi~χ2(3),易知其为WOD样本. 模拟分析结果如表1所示,通过模拟分析可以看出,不论是独立样本还是相依样本, VaR核估计和样本分位数估计的平均偏差均随着样本增大而减小,前者在各样本量上的偏差均要显著小于后者.此外,对比独立样本和相依样本发现,VaR核估计的优势在相依样本上表现突出. 表1 VaR估计平均偏差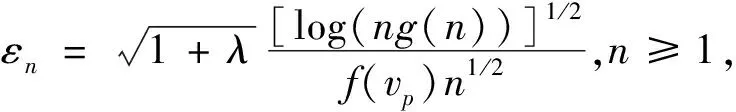






2 数值模拟分析