基于多元联合分布函数的托辊综合质量评价方法

倪永帅 黄 璜 罗克松

北京起重运输机械设计研究院有限公司 北京 100007

0 引言

托辊是带式输送机的重要部件，其成本占一台带式输送机总成本的20% ～35%，承受了70%以上的阻力，托辊的质量尤为重要[1,2]。由于托辊行业生产技术不断提高以及下游需求市场不断扩大，我国托辊行业近年来发展速度较快。但由于生产条件各不相同，不同厂家生产的同类型、同型号、同规格的托辊性能参数差异较大[3]，同一厂家不同批次的产品也存在一定差异。通过样本试验得到托辊技术参数，进而分析某批托辊的综合质量，不仅有利于对不同厂家托辊质量进行横向比较，也有利于企业比较分析不同批次产品的优劣程度。但是，在MT 821—2006《煤矿用带式输送机 托辊 技术条件》中，检验托辊性能的技术指标有13项[4]，其中量化指标有9项，且各项指标的重要程度不同。在做一批托辊质量综合分析时，不宜仅依靠单项指标作为判断标准。因此，引入综合评价参数将有利于做出更为直观的判断分析。本文介绍一种基于多指标的联合分布函数的数学模型，从统计学的角度引入一个综合评价参数，并通过综合评价参数的概率分布来分析一批托辊的综合质量。

1 数学模型

设同一批同规格、同型号、同类型的托辊为S，设随机变量I1，I2，…，Ij为托辊的技术指标，当同批次托辊足够多，且各技术指标方差有限时，根据中心极限定理[5]，每一个随机变量Ii应满足正态分布，取随机变量Gi为Ii的评价变量，且Gi也满足正态分布。从集合S中抽取若干样本来进行试验，通过实验取得样本数据，从而得到各个随机变量正态分布的参数。构造一个新的随机变量R，R=fs(G1,G2,…,Gj)。R即为综合评价参数。

1.1 各技术指标的的概率分布

由于托辊各技术指标的表现形式各不相同，需要用评价变量Gi将其值进行统一。本文选取百分制评分的方式将其统一，对于评价托辊的单项技术指标，MT 821—2006《煤矿用带式输送机 托辊 技术条件》给出了允许值[4]，将允许值Iallow定为60分，即Gallow= 60，理想值Iideal定为100分，即Gideal=100，则Ii的评价变量Gi为

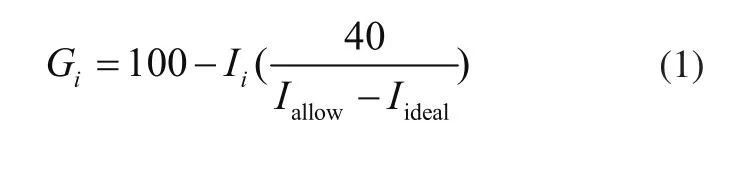
为得出R的分布，首先研究每个独立随机变量Gi情况。抽取n个被测托辊作为样本，可测得一组Ii的样本，变换得到Gi的样本。因为正态分布是一个稳定分布，根据中心极限定理，Ii服从正态分布，则Gi也服从正态分布。若该正态分布的均值为μ、方差为σ2，即Gi～N(μ,σ2)，则Gi的概率密度函数[5]为

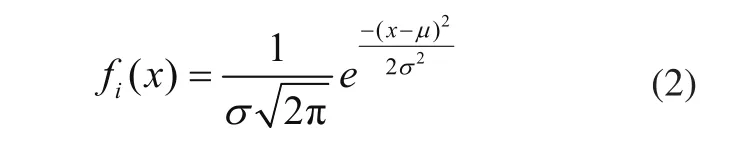
对于每一组随机变量Gi，可以写出相应的概率密度函数fi(x)。

1.2 综合评价参数R

引入综合评价参数R，随机变量R的函数fs(G1，G2，…，Gn)可以根据实际经验确定，本文采用计算加权平均值的方法，即

式中：ai为每项技术指标的权数。

1.3 综合评价参数R的概率密度

为得到R的概率密度函数，先求得Gi的联合概率密度函数，设Gi的概率密度函数为fi(x)，由于G1，G2，…，Gn是独立的，则其联合概率密度函数为[5]

然后对f1(x1)、f2(x2)和f3(x3)进行计算，此时r2=a1x1+a2x2+a3x3=r1+a3x3，可以转化为f(r1)和f3(x3)2项的计算，其概率密度函数为

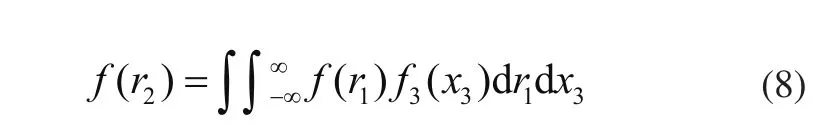
重复上述计算过程，最终得到R的概率密度函数f(r)。

由f(r)作图，可以直观地分析出各组样本托辊的综合质量。由于样本与总体S同分布，进而可以得出该批托辊的综合质量。文分别选取A厂和B厂10个同类型、同型号、同规格（Φ133×380）的托辊样本对上述结论进行验证。

2 实验及结果分析

MT 821—2006《煤矿用带式输送机 托辊 技术条件》中给出了9个托辊技术参数的量化指标[4]，分别是径向圆跳动、旋转阻力、轴向窜动、轴向载荷、跌落强度、浸水密封、煤尘密封、使用寿命、淋水密封。本

2.1 两项技术指标综合评价参数计算

选取旋转阻力I1和轴向窜动I22项技术指标来对2厂的托辊质量进行评价，具体数值见表1，设2个指标的权数各为1/2。

表1 A厂和B厂的技术参数

根据MT 821—2006《煤矿用带式输送机 托辊 技术条件》，该规格托辊旋转阻力的允许值为3.0，理想值为0，轴向窜动的允许值为1.2，理想值为0，则根据式（1），可分别得到A厂和B厂的评价变量G1、G2、G1＇、G2＇，见表2。

表2 A厂和B厂技术参数的评价变量

由此可得各组G值正态分布参数，见表3。

表3 A厂和B厂技术参数评价变量正态分布参数

r=x1/2+x2/2，根据式（2）和式（7），可以得到2组概率密度函数，分别为

计算可得

由概率密度函数可得图1，图中横坐标为基于2项技术指标的托辊综合评分，纵坐标为该评分对应的概率值。图中反映了所选取的10个托辊样本中每个分值的的概率和样本总体（即该厂生产的同批次产品）中不同分值的分布情况。从图1中可以直观地看出，A厂综合指标优于B厂。其中A厂以综合评分在75 ～80分的产品居多，B厂则以综合评分在65 ～70的产品居多。此外，综合评分在60分以下的产品B厂多于A厂，即B厂出现不合格品的概率大于A厂。

图1 2厂2项指标概率分布图

2.2 3项技术指标综合评价参数计算

为了进一步对该模型进行验证，又增加了一项技术指标，选取旋转阻力I1、轴向窜动I2和径向圆跳动I33项技术指标来对A、B厂的托辊质量进行评价，设3项指标的权数各为1/3，A厂和B厂的径向圆跳动数据见表4。

表4 A厂和B厂托辊样本的径向圆跳动

根据MT 821—2006《煤矿用带式输送机 托辊 技术条件》，该规格托辊径向圆跳动的允许值为0.7，理想值为0，根据式（1），可分别得到A厂和B厂的评价变量G3和G3＇，见表5。

表5 A厂和B厂径向圆跳动评价变量

由此可得各组G3和G3＇的正态分布参数，见表6。

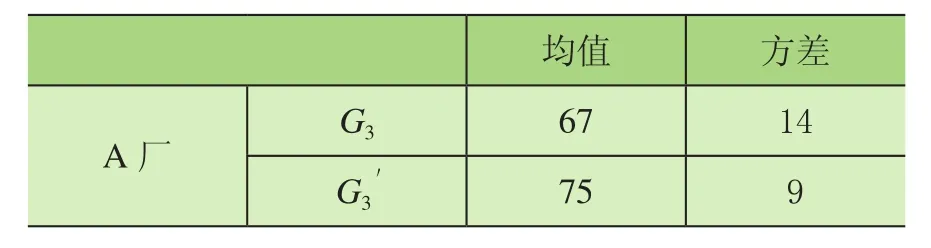
表6 A厂和B厂技术参数评价变量正态分布参数

首先计算旋转阻力和轴向窜动2项指标的综合评价参数，方法见2.1节，这里r1=x1/2+x2/2，可得式（11）和（12）。

然后引入径向圆跳动计算3项指标的综合评价参数。由式（2）可得

代入式（8）,这里r= 2r1/3+x3/3，即r1=3r1/2-x2/2可以得到2组概率密度函数

由概率密度函数可得到图2，图中横坐标为基于3项技术指标的托辊综合评分，纵坐标为该评分对应的概率值。从新增的技术指标来看，B厂的径向圆跳动值要显著优于A厂，其平均值更高且方差更小。但是，综合3项指标，A厂的产品质量仍然优于B厂。其中A厂以综合评分在70 ～80分的产品居多，B厂则以综合评分在65 ～75的产品居多。由此可见，仅根据一项指标来评价一批产品的优劣是片面的，并不能反映该批次产品的综合质量。随着模型中所考虑的技术指标的增多，综合评价参数对产品综合质量的分析也更加准确。

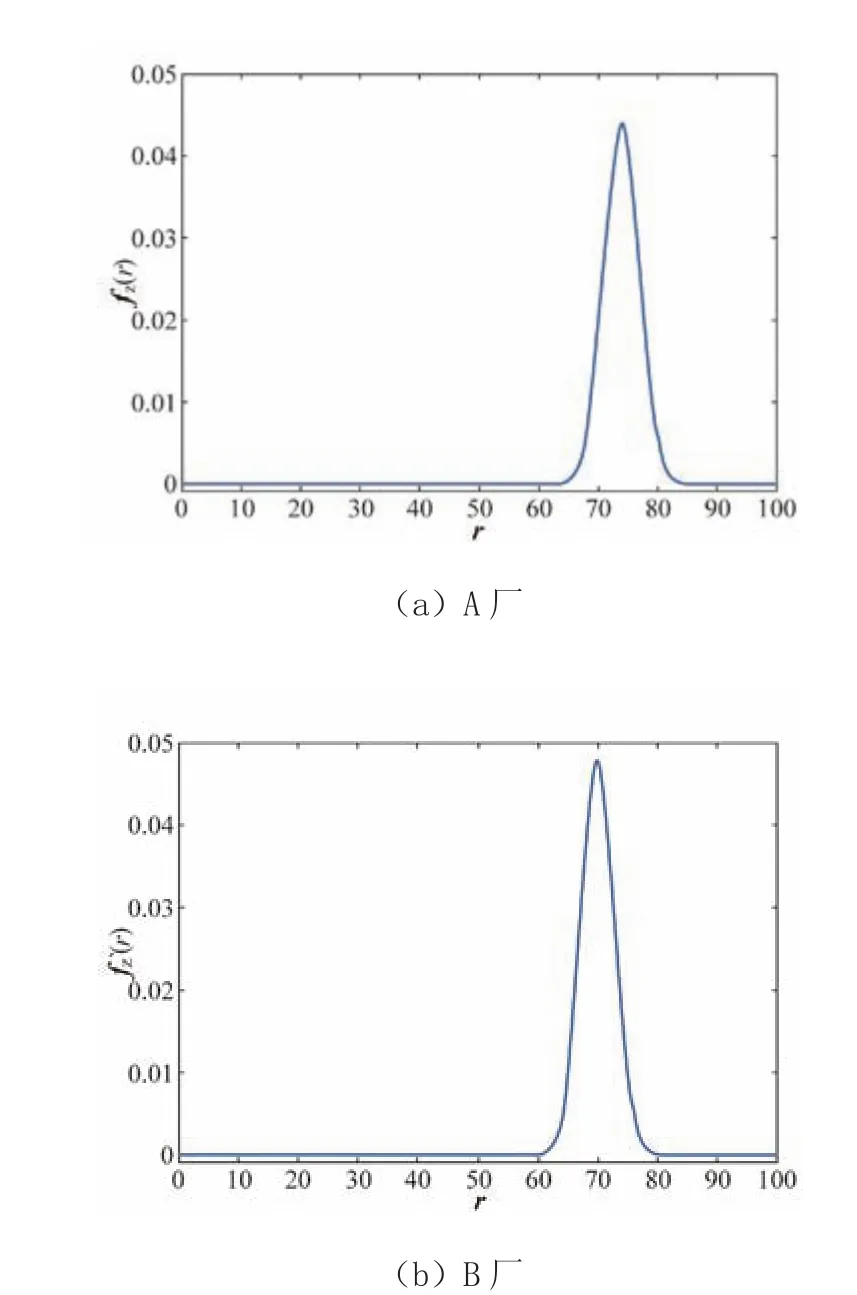
图2 2厂2项指标概率分布图

3 结论

本文引入了综合评价参数R，提出了一种将多元指标联合用于托辊综合质量评判的方法。该方法利用抽取样本的实验结果从统计学角度不仅能够反映同一批产品的质量分布情况，也能够对比不同厂家的产品分析其质量的优劣。通过计算，本文给出了综合评价参数概率密度的解析形式，并画出了相应的概率分布图，直观地对综合评价参数各分值的概率进行了分析。在实际应用中，可根据经验值改变综合评价参数函数或各项指标的权数。本文仅给出了基于2项指标和3项指标的综合评价参数的详细计算过程，若要引入更多指标，可参照上述过程逐步进行计算。该数学模型的建立以及综合评价参数的引入为托辊综合质量的分析提供了一种更全面更准确的评价手段。