基于概率密度函数的控制系统性能评价
2014-08-02钟振芳刘吉臻孟庆伟牛玉广
钟振芳 刘吉臻 孟庆伟 牛玉广 房 方
(华北电力大学控制与计算机工程学院,北京 102206)
在工业控制领域中,生产过程的控制回路不断增加,生产工艺对生产过程的控制要求也日益提高。大多情况下,人们往往只关注采用怎样的控制器和怎样的控制策略,而忽视了运行中的控制系统性能评价研究。据统计,在当前的工业控制系统中,有多达60%的控制器存在着性能差的问题[1]。若能对工业控制系统的性能进行有效地评价,将提高工作效率、降低生产成本、提高控制的有效性。所以,进行控制系统性能评价方法的研究是必要的。
关于控制系统性能(尤其是随机性能)的研究主要集中在方差分析上。1989年Harris T J提出基于反馈不变项的最小方差(Minimum Variance,MV)性能评价指标之后,围绕方差对控制系统进行的性能分析不断得到发展[2]。最小方差性能指标被相继应用在前馈控制系统[3]、串级控制系统[4]、非最小相位系统[5]和多输入多输出(Multiple-Input Multiple-Output,MIMO)系统[6]中。最小方差对传统PID控制器和先进控制器(如预测控制)的性能评价也得到了广泛的应用[7,8]。此外,还有一些基于最小方差的性能指标被相继提出,如:基于开环方差的相关方差(Relative Variance Index,RVI)指标[9]、结合控制量约束的广义最小方差(General Minimum Variance,GMV)[10]。
相较于方差,概率密度函数对系统输出的随机性能有着更为全面的描述,因此基于概率密度函数的性能评价具有重要的研究意义。基于概率密度函数的随机控制是通过控制系统跟踪误差的概率密度函数来实现对系统的有效控制的。期望跟踪误差的概率密度函数分布可以是高斯分布(正态分布)、均匀分布或者某种自定义的分布,这是根据具体的控制要求来给定的。因为以高斯分布做概率密度函数期望分布在日常生活中普遍存在,而且具有一定的广泛性(电解铝的控制、化工过程分子量的空盒子、铸件尺寸及灯泡的大小等),所以在通常情况下将控制变量设计成服从高斯分布。由于当前控制下系统跟踪误差的概率密度函数分布很可能不是最优的,其与最优分布的距离就可以用来评价当前控制性能的优劣。两个函数比较其之间的差距,首先要提取其关键特征,故笔者先将概率密度函数向量化使对概率密度函数的分析转化为对两个向量的分析。为得到归一化、规范化、易于理解的性能评价指标,灰色关联分析被用来比较实际分布向量和基准向量之间的近似程度。*收稿日期:2013-12-16(修改稿)基金项目:国家重点基础研究发展计划项目(“973”计划)(2012CB215203);国家自然科学基金重点资助项目(51036002);国家自然科学基金资助项目(61203107);中央高校基本科研业务费资助项目(12QX19);北京市教育委员会共建项目
笔者首先给出了最优概率密度函数分布,然后基于实际输出的分布与最优概率密度函数分布通过灰度关联法定义出性能评价指标,最后应用该指标对控制系统进行评价。
1 最优概率密度函数
为了评价控制系统的性能,要求首先给出性能评价的基准。而性能评价的基准需要满足两个要求:理论上是某个性能的界限;能通过实际闭环操作数据估计得到。
1.1 最优概率密度函数的控制
对于常见的线性控制系统:
(1)
其中yk为k时刻的输出,uk为k时刻的控制量,ωk为随机扰动。其控制误差为:
ek+q=yk+q-rk+q
(2)
=f(y,u,r,ωk)
其中y为系统输出向量,y=(yk,yk-1,…,y1);u为控制向量;e为误差向量;r为设定值。若随机噪声ωk服从高斯分布N(μ,δ2),μ和δ分别为期望和标准差,则随机噪声的概率分布函数如下:
(3)
由概率论易得,跟踪误差的概率密度函数为:
(4)
由式(2)~(4)可得:
(5)

为获得最优分布的概率密度函数,笔者采用最小熵控制,在最小熵控制下,可得控制系统的递推控制律[11]:
(6)
式(6)可以改写为:
b0uk+ηk+q=b0uk-1+ηk-1+q=c
(7)
其中c为常数,则可得控制律如下:
(8)
取c=μ,将式(8)代入式(5)可得在最小熵控制下跟踪误差的概率密度函数为:
(9)
可知此时最优概率密度函数服从高斯分布N(0,δ2)。
1.2 最优概率密度函数的估计
由1.1节可得最优的概率函数(式(9)),其中需要估计的量只有一个,就是δ,即噪声的方差。
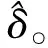
(10)
1.3 跟踪误差概率密度函数的估计
系统的性能评价就是系统当前性能与基准性能的比较过程。在得到基准性能之后,需要计算系统的当前性能,即计算跟踪误差的概率密度函数。跟踪误差的概率分布计算式为:
(11)
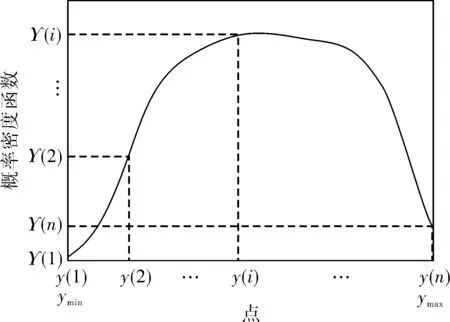
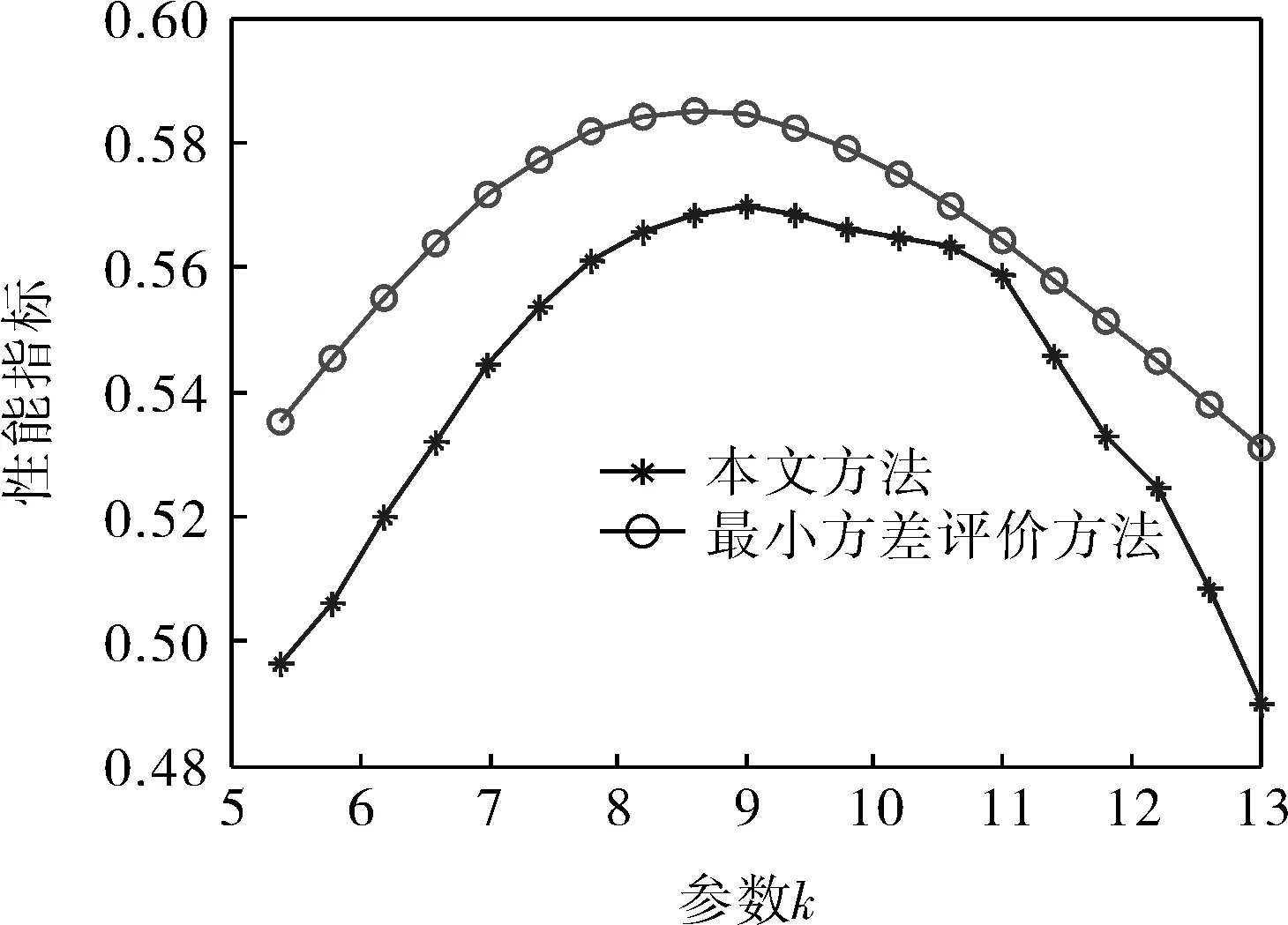
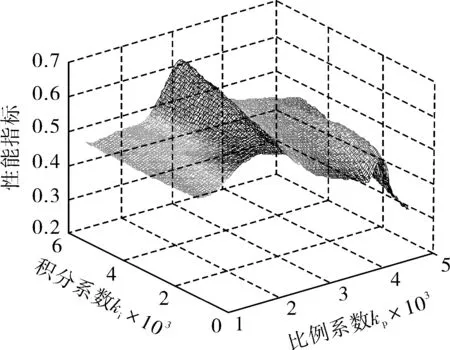
其中,N表示总的采样数据的个数,Num(ei 跟踪误差的概率密度函数的计算式为: (12) 其中,ΔF为采样数据的变化量,Δe为误差的变化量。对于跟踪误差的概率密度函数可以多项式逼近的方式来表示: (13) 其中,γ(e,u)为系统输出的概率密度函数,Si(e)为定义在输出区间上的基函数,ωi(u)为基函数权重,ε为逼近误差。 式(13)的逼近中有一个主要的限制来自于概率密度函数的定义。对于定义在区间[p,q]上的概率密度函数,其一定满足如下条件: (14) 对于输出的概率密度函数的估计,可以通过最小二乘进行多项式逼近,也可以通过B-spline进行逼近求得[13],只是基函数的选择不同而已。 在第1部分中给出了最小熵控制下的控制误差的最优概率密度函数。该最优概率密度函数作为标准可实现对控制系统的性能评价。 定义如下的性能指标: 对系统实际输出的概率密度函数可以通过一个向量来近似表示。求输出的最大值ymax与最小值ymin,在区间[ymin,ymax]上取n个等间距的点(图1)y(1),y(2),…,y(i),…,y(n),其中y(1)=ymin,y(n)=ymax。令Y=[y(1),y(2),…,y(i),…,y(n)],其对应的概率密度函数可由如下向量近似表示: Υ=[Υ(1),Υ(2),…,Υ(i),…,Υ(n)] (15) 当n趋向无穷大时,概率密度函数和其表示向量在一定输出范围内完全相等。在一定输出范围内,要比较两个概率密度函数的近似程度,可以通过比较两者在该范围内的向量的Υ不同来表示。 图1 概率密度函数向量化示意图 根据本节给出的最优概率密度函数转化为向量的办法,可得最优概率密度函数的表征向量如下: (16) 按照灰色关联分析理论。首先求向量差: (17) 求其最大值: ΔΥmax=max[ΔΥ(i)] (18) 求其最小值: ΔΥmin=min[ΔΥ(i)] (19) 则此时的性能评价指标可以写为: (20) 显然该指标满足规范性和接近性的要求。其中ζ为分辨率,ζ∈[0,1]。 笔者所提方法可以在不干扰控制系统正常运行的情况下完成性能评价。在此无侵入性的要求下,希望通过闭环操作数而不是通过做性能试验的方法来确定控制系统的性能。利用闭环操作数主要是通过如下步骤来完成性能评价: a. 通过设定值与系统输出计算控制系统的跟踪误差; b. 通过白化过程估计噪声的方差; c. 通过式(10)计算最优分布的概率密度函数; d. 通过跟踪误差计算其概率密度函数; e. 通过式(15)给出实际概率密度分布的表示向量; f. 通过式(16)计算最优分布的概率密度函数的表示向量; g. 通过式(20)计算系统性能指标。 对于如下的过程: 其中αt为某一均值为0、方差为0.5的白噪声。采用如下的PI控制器: 其中kp=0.001,ki=0.002。在控制器参数不变的情况下,系统的特性发生变化时,控制系统的性能将会发生变化。当k在5~13之间变化时,系统的性能变化如图2所示。可以看出,虽然笔者性能评价的计算值与最小方差性能评价的计算值不同,但是可以得出相似的评价结果,这就验证了笔者方法的有效性。随着k的增大,系统的控制性能先增后减。 图2 系统的性能随k值的变化 同样当k取定为9时,使PI控制器的比例系数和积分系数变化,系统的性能变化如图3所示。可以看出,在ki不变时系统的性能随着kp的增加先升后降;而在kp不变时,随着ki的增加系统的性能变化不大。这就是说明,系统的随机性对比例作用更敏感,也就是说要想得到较好的随机性能要更加重视比例系数的调整。从图3中还可以看出,在kp=3时系统的性能出现一道“山脊”,该“山脊”对应着系统随机性能较好的情况。这样图3实际上为PI控制器的性能评价提供了较为全面的参考,对PI参数优化指出了方向。 图3 k=9时系统的性能变化 笔者提出了一种基于概率密度函数的性能评价方法,给出了线性控制系统最优的概率密度分布,通过灰色关联分析构建了新的随机性能评价指标,还给出基于该指标的性能评价一般性步骤。该方法在性能评价过程中无需进行性能实验,仅仅需要控制系统的闭环操作数,对控制系统的正常运行无干扰,利于在实际工业过程中进行应用。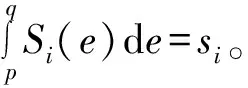
2 性能评价
2.1 性能指标
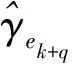
2.2 基于灰色关联的性能指标构建
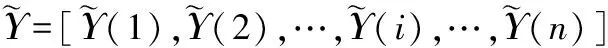
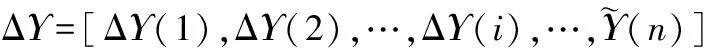
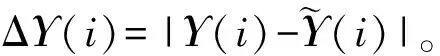
2.3 性能指标完成步骤
3 仿真实验
4 结束语
