基于位移置换法的超静定梁变形解析计算*

李银山 刘灿昌 王新筑 李欣业

1河北工业大学机械工程学院 天津 300401 2山东理工大学交通与车辆工程学院 淄博 255000 3重庆大学航空航天学院 重庆 400044

0 引言

梁的变形计算是现代设计的重要内容之一，其计算方法有解析法和数值法2种，但其均存在解的结构复杂、计算量大等问题，增加了工程计算成本[1-4]。能量法和力矩—面积法能较快计算梁特定点的变形, 但该方法计算量大，难以应用到复杂载荷作用的梁变形计算，限制了其在复杂载荷环境的工程应用。共轭梁法避免了积分的计算, 但却无法适用于载荷复杂的问题。喻晓今[5]利用置换法求解一端外伸梁变形，提出一种基于叠加无需积分的变形计算方法；彭如海[6]研究了梁上特殊点的位移置换函数，提出一种求解梁的变形位移置换方法。

计算机代数系统在工程计算和计算机辅助教学等领域得到广泛应用[7-16]；高云峰、李银山、阿鲍夫斯基 H Π等[17-20]利用连续分段独立一体化积分法得到位移置换函数，通过计算机软件符号计算得到解析解，发展了一种计算机辅助计算方法；王小明[21]以加筋板中板与筋的耦合力和力矩为中间未知量，提出了一种板筋分离法的计算方法。

本文利用位移置换法求解了复杂载荷作用下超静定梁任意一点的挠度、转角和弯矩，利用位移互等定理求解了单位力作用下的互等位移，通过变形叠加方法计算复杂载荷作用下超静定梁任意一点变形，推导多边界、多载荷作用下的超静定梁位移置换函数，通过位移置换法给出梁变形解析解，利用Maple程序计算任意节点位移数值，得到超静定梁变形曲线。

1 位移置换法

1.1 位移置换法

由位移互等定理可知，若分别在横坐标ξ和x处作用单位力F0＝1 (见图1a)，则在ξ处的单位力引起x处的位移δq（x；ξ）与在x处的单位力引起ξ处的位移δq（ξ；x）应相等，即

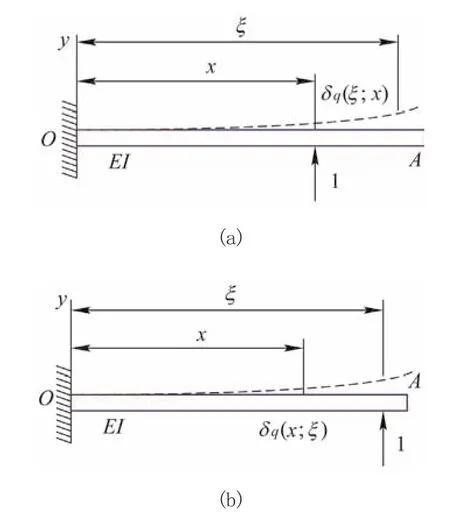
图1 位移互等定理

设梁上作用分布力q（x），分布弯矩m（x），在ai处的集中力Fi，在bi处的集中力偶矩Mei。则点ξ的挠度v（ξ）为

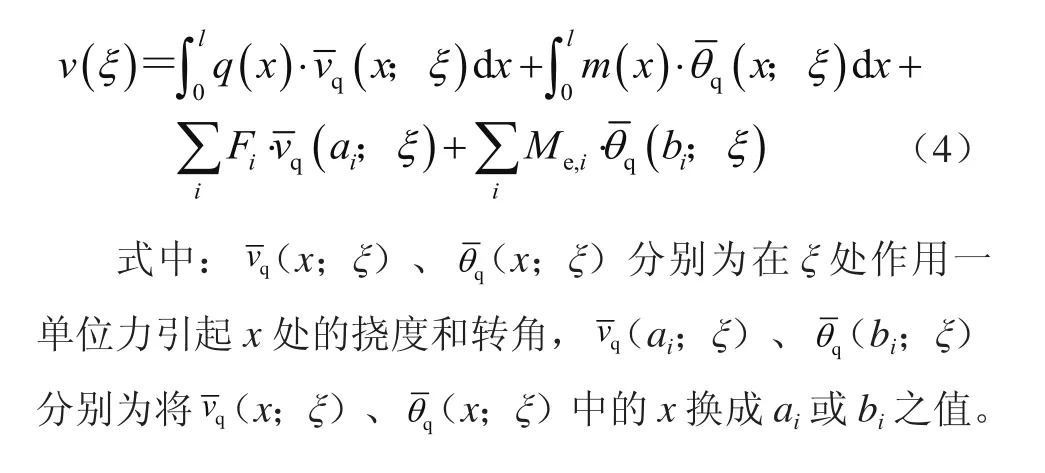
1.2 超静定梁的位移置换函数

由图2可知，给出超静定梁的3种情况下δq（x；ξ）的表达式。

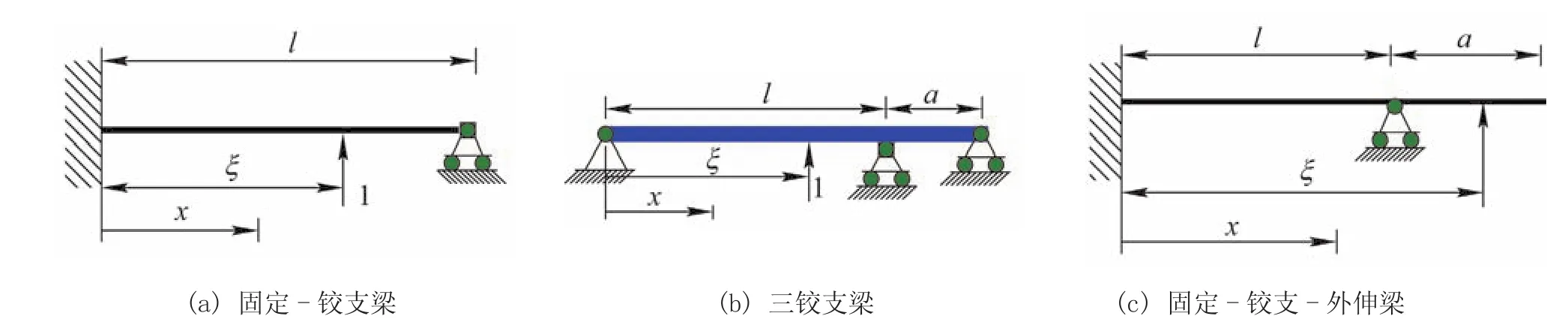
图2 超静定梁位移置换函数计算示意图

1）固定-铰支梁

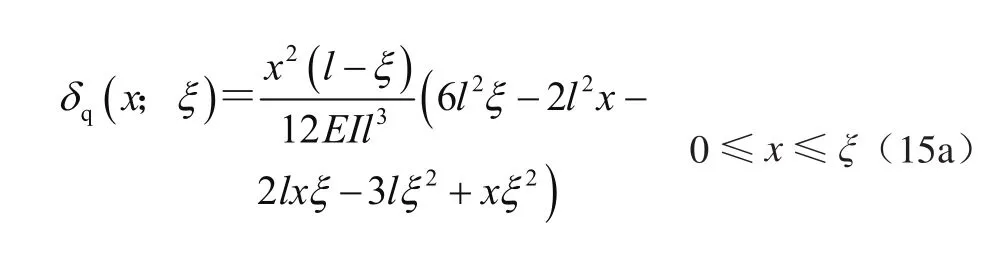
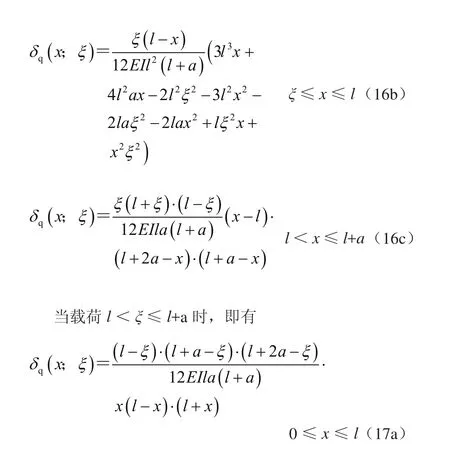
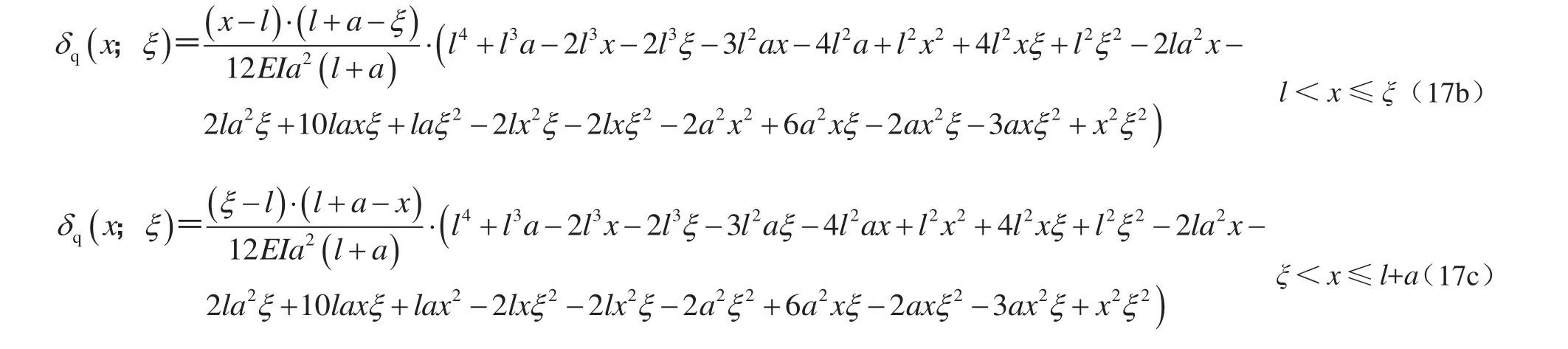
3）固定-铰支-外伸梁

当载荷在0≤ξ≤l时，即有

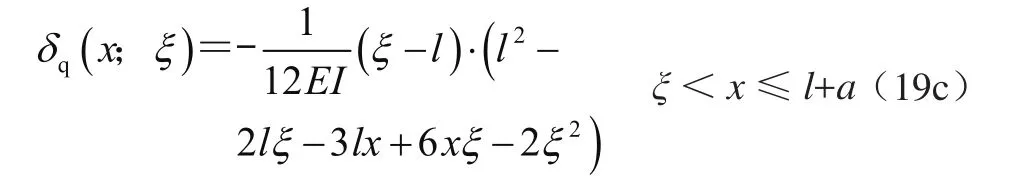
综上所述，位移置换函数可采用连续分段独立一体化积分法快速得到。

2 工程实例

1）实例1

如图3所示，受均布载荷的固支-铰支梁，试求B点的转角。已知梁弯曲刚度EI为常数，用位移置换法求解。

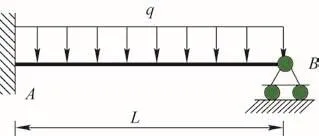
图3 固支-铰支梁受力简图

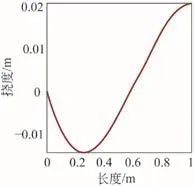
图4 转角图

2）实例2

如图5所示，受复杂载荷三铰梁，试求D点的挠度。已知梁各段弯曲刚度EI为常数。已知：L=8 m，q=4 kN/m，F=qL/4，a=L/2，用位移置换法求解。

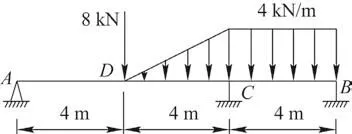
图5 受复杂载荷三铰

①载荷函数

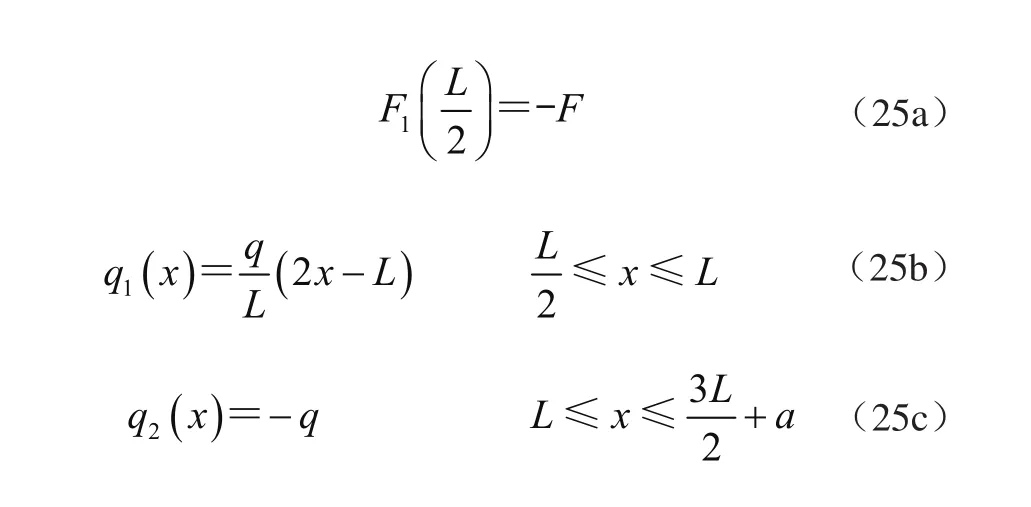
②求单位力作用下的挠度

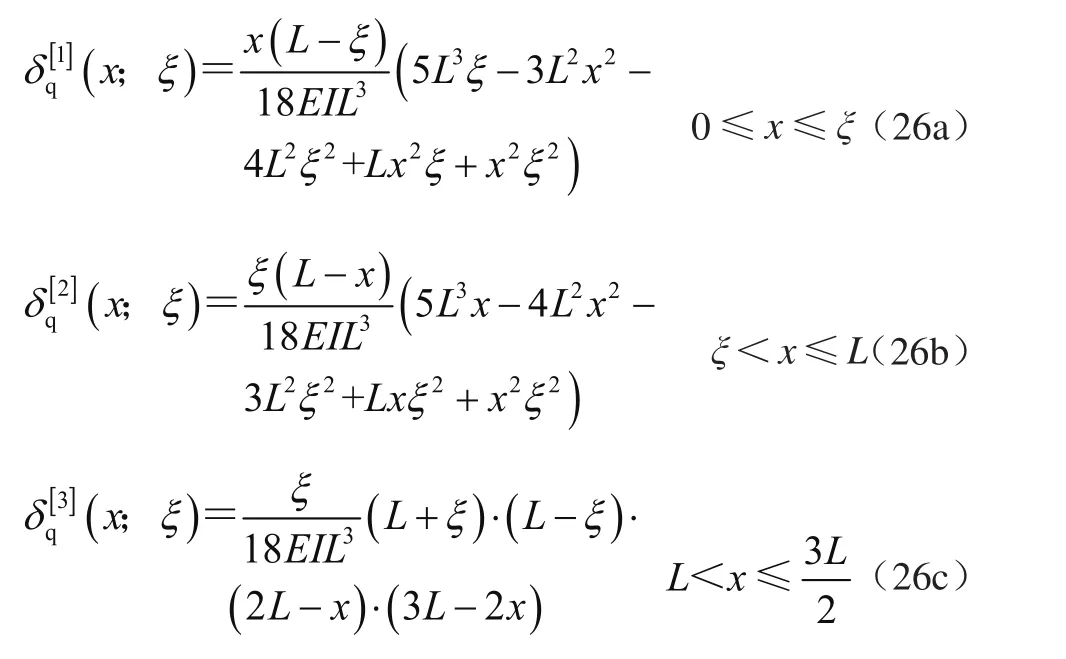
③求外载荷作用下的挠度函数

挠度函数(见图6)为

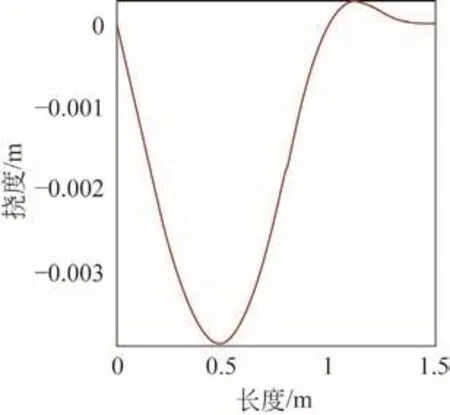
图6 挠度图

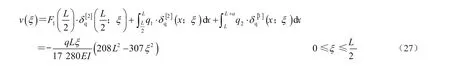
④求D点的挠度

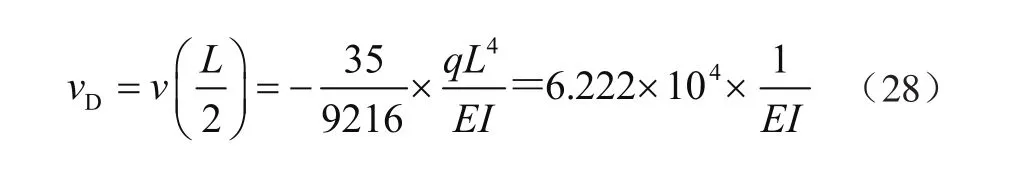
3）实例3

如图7所示，受复杂载荷的固定-铰支-外伸梁，试求A点和D点的弯矩。已知梁各段弯曲刚度EI为常数。已知：L=6 m，q=3 kN/m，F=（5/9）qL，a=L/2，用位移置换法求解。

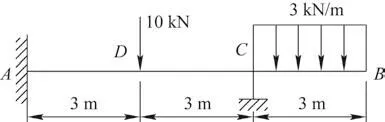
图7 固支-铰支外伸梁

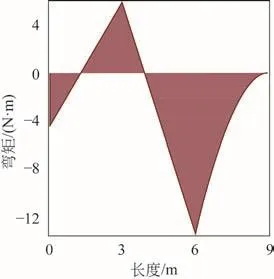
图8 弯矩图

3 求超静定梁的位移置换函数

以固支-铰支梁为例，介绍连续分段独立一体化积分法求位移置换函数的步骤如下：

1）本题分为2段，即n=2，各段的挠曲线近似微分方程为

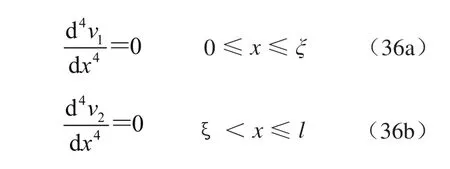
2）积分1次得剪力方程的通解；

3）积分2次得弯矩方程的通解；

4）积分3次得转角方程的通解；

5）积分4次得挠度方程的通解；

6）根据边界条件和连续光滑条件确定积分常数为

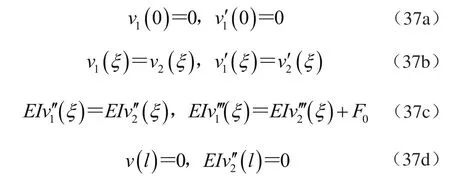
7）求挠度函数

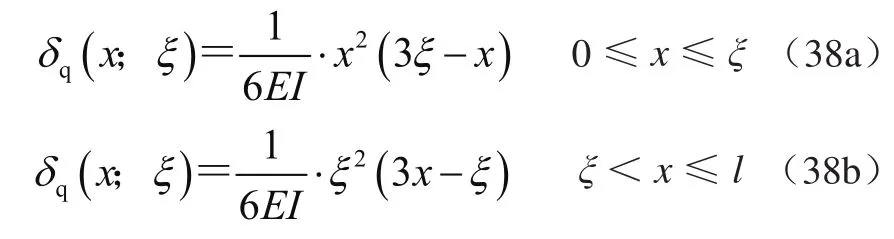
4 结论

本文将位移置换法由求解梁特定点变形计算推广到一般点的变形计算，发展了梁变形计算方法，给出了一种超静定梁变形计算的简化方法。同时，研究了位移置换函数确定方法，给出了各种边界超静定梁在复杂载荷作用下位移置换函数，利用位移置换法给出梁变形解析解，并利用Maple程序计算任意节点位移数值，得到超静定梁变形曲线。