采用斜距波数子带划分的SAR图像自聚焦方法

马彦恒， 褚丽娜， 杨晓亮， 侯晓泽

(1.陆军工程大学 石家庄校区，河北 石家庄 050003；2.中国电子科技集团 第五十四研究所，河北 石家庄 050000)

小型旋翼无人机载合成孔径雷达(small rotor unmanned aerial vehicle synthetic aperture radar, SRUAV-SAR)可全天时、全天候，灵活有效地获取观测区域的二维高分辨图像[1-3]。SRUAV-SAR平台易受大气湍流等因素的影响，偏离理想运动轨迹[4]，不再满足方位不变假设，导致SAR图像的散焦和几何失真[5-6]，传统的频域处理算法[7-10]不能达到良好的聚焦性能。时域反向投影(back-projection, BP)[11]算法沿斜距历程对成像网格上的每个像素点进行积分重构，较好地解决了距离-方位耦合的问题。BP算法对轨迹、带宽、积累角等成像条件没有限制，且没有方位不变假设，更适用于SRUAV-SAR成像。但是，BP算法计算量大，成像效率低，快速因子分解BP(fast factorized BP, FFBP)算法以递归的方式显著地减少了计算负担，并保持了BP算法[12]的准确性和适用性。FFBP算法可以通过并行处理器硬件实现，在机载SAR成像领域具有广阔的应用前景[13]。

通常，可以将运动误差对SAR图像的影响分为非系统距离单元徙动(non-systematic range cell migration, NsRCM)和方位相位误差(azimuthal phase errors, APE)[14]，前者导致距离向散焦，影响APE自聚焦的性能，后者导致方位向聚焦退化。传统的运动误差补偿方法是采用机载惯性导航系统(inertial navigation system, INS)和全球定位系统(global positioning system, GPS)直接测量的运动偏差在SAR成像之前进行APE和NsRCM补偿。但是，SRUAV-SAR平台的载荷能力有限，难以搭载高精度的运动传感器，并且现有运动传感器的精度也达不到高波段SAR成像精度要求[14]。因此基于回波数据的自聚焦技术对于SRUAV-SAR成像非常重要。

相位梯度自聚焦(phase gradient autofocus, PGA)[15]充分利用了图像域与相位历程域之间的快速傅里叶变换(fast Fourier transform, FFT)关系，是一种高效的空间不变相位误差估计自聚焦方法。文献[16，17]将基于拟极坐标系(quasi-polar grid, QPG)的FFBP成像和PGA或基于加权的PGA(weighted PGA, WPGA)相结合，实现了基于回波数据的图像自聚焦，但未考虑沿方位向运动误差；文献[18]将FFBP与自动校准结合用来处理机载SAR数据，但没有考虑NsRCM补偿；文献[19]通过一致修正NsRCM和APE来实现补偿，但未考虑运动误差的空变性。因此，基于无人机二维空变运动误差校正的SAR数据自聚焦仍是一个亟待解决的问题。

本文提出一种斜距波数子带划分的SAR图像自聚焦方法，用于SRUAV-SAR数据无INS自聚焦成像处理。首先基于QPG-FFBP成像模型，分析运动误差在波数域的空变特征；然后基于时域到波数域的映射关系，推导NsRCM和APE的关系式，用于多子带NsRCM补偿；最后仿真和实测数据结果验证该方法的有效性。

1 拟极坐标系SAR成像模型

1.1 SAR平台运动模型

直角坐标系中无人机载SAR的几何关系如图1所示。图中，X轴表示方位向，Y轴表示距离向，Z轴表示高度向，O为整个合成孔径天线相位中心(antenna phase center, APC)时刻。理想飞行轨迹用绿色实线表示，与X轴重合，Ai为ta时刻理想轨迹的APC位置；实际飞行轨迹用红色虚线表示，为不规则的曲线，Ar为ta时刻实际轨迹的APC位置。P是地面波束覆盖区中任意一点，Ri和Rr分别表示ta时刻SAR到P点的理想和实际瞬时斜距。则P点的斜距误差为

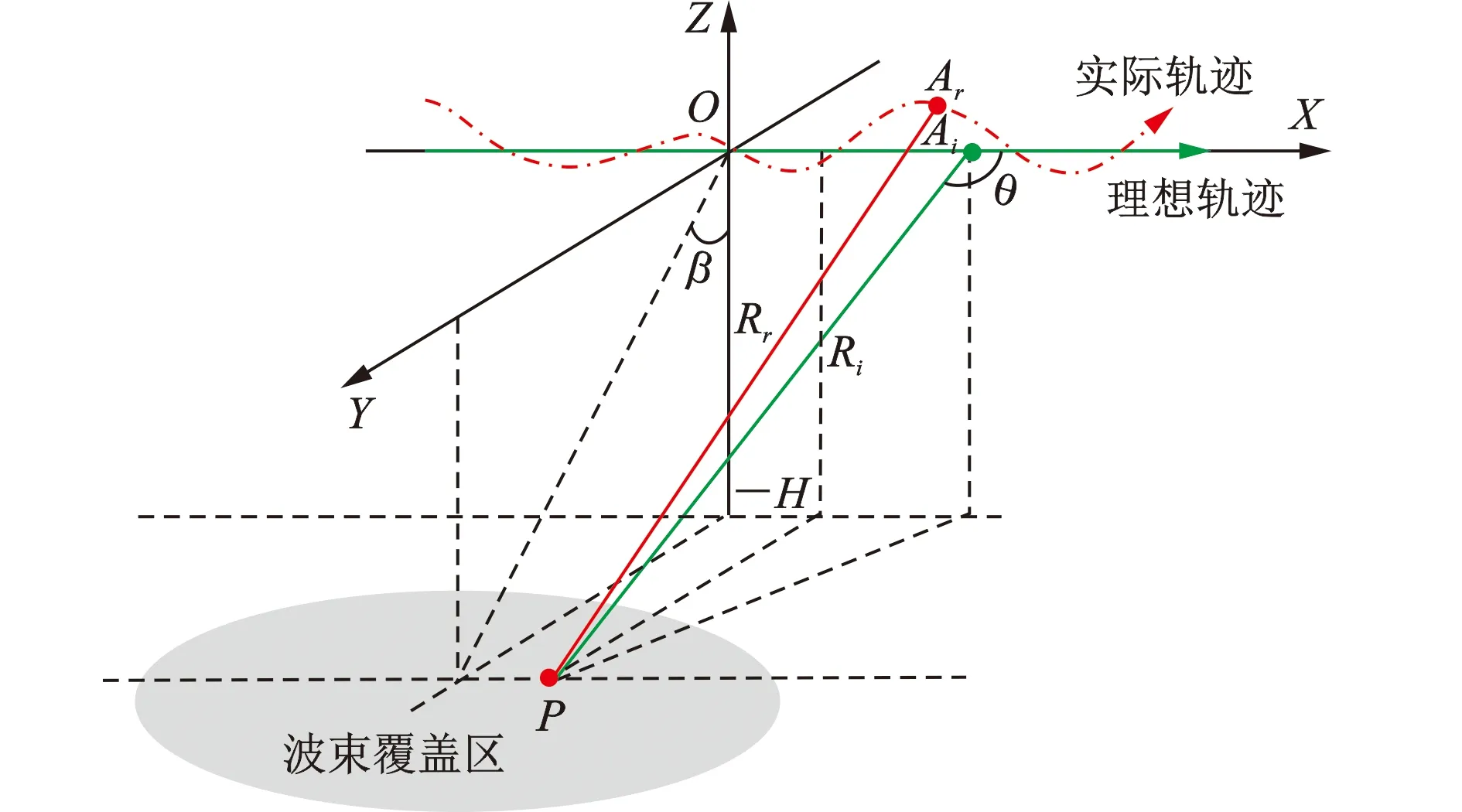
图1 机载SAR几何关系

设理想轨迹OAi=[xi(ta),yi(ta),zi(ta)]T，实际轨迹OAr=OAi+AiAr，其中AiAr=[Δx(ta),Δy(ta),Δz(ta)]T，表示实际轨迹与理想轨迹的轨迹偏差；P点坐标OP=[x0,y0,-H]T，其中H表示实际轨迹距离地面的高度。代入式(1)得

其中

则

ΔR(ta;x0,y0)=

Ri(ta;x0,y0)

(4)

式中：Δx(ta)≪Ri(ta;x0,y0)，Δy(ta)≪Ri(ta;x0,y0)，Δz(ta)≪Ri(ta;x0,y0)。忽略式(4)中的轨迹偏差的高次项，得

根据图1中的几何关系可得

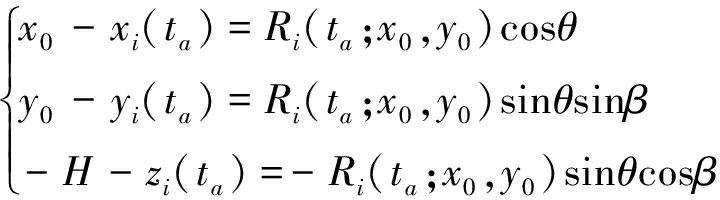
(6)

式中：θ表示瞬时斜视角，β表示APC的入射角。将式(6)代入式(5)，运动误差可近似表示为

由于三维轨迹偏差中θ和β的存在，使得不同位置目标点的斜距误差ΔR(ta;x0,y0)具有空变特性，传统的自聚焦方法不再适用。

1.2 拟极坐标系下SAR成像模型

Bao等[20-24]在拟极坐标系下分析了运动误差引起的方位相位误差和距离徙动间的关系，并在图像谱域推导APE和NsRCM之间的关系，与FFBP算法结合可实现NsRCM补偿，在无INS情况下基于回波数据进行运动误差补偿，显著提高图像聚焦的质量。但该方法将图像波数域的相位误差线性映射到方位时域，这种空间不变的线性近似并不总能成立。

在此只考虑适用于自聚焦的聚束SAR或子孔径SAR回波数据。点目标P和直角坐标系、拟极坐标系之间的几何关系如图2所示。其中：X为方位向，Y为斜距向；Ac为子孔径APC中心，坐标为[xc,yc]T；Ai为雷达在子孔径内运动的位置，坐标为[xi(ta),yc]T；P为雷达照射区域内任意一点，直角坐标系坐标为[x0,y0]T，拟极坐标系坐标为[r0,cosθ0]T，r0表示斜距平面内子孔径中心Ac到目标点P的斜距，cosθ0为子孔径中心斜视角θ0的余弦。由图2可知，参数间有如下关系

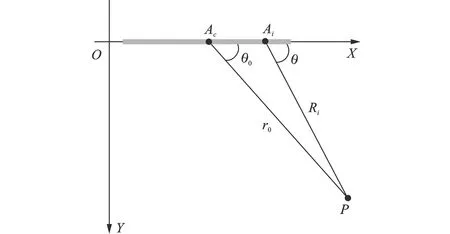
图2 斜距平面拟极坐标系和直角坐标系的几何关系

(8)

当无高精度INS用于运动误差补偿时，Ai即为理想运动轨迹，根据余弦定理点P的理想瞬时斜距为

设Δxi(ta)=xi(ta)-xc，则

点P的瞬时斜距可表示为

设SAR回波为线性调频信号，经距离压缩后可表示为

式中：fr=γ·tr表示距离频率，与距离向快时间tr呈线性关系，γ为常数，表示频率变化率；Br为信号带宽；ta为方位向慢时间，tc表示当前子孔径中心时刻，Ts为当前子孔径波束照射时间。式(11，12)中相位误差可表示为

点P的拟极坐标FFBP成像可表示为

将式(11)代入式(14)，整理得

由式(10)可得

将式(16)在r=r0,cosθ=cosθ0处进行一阶泰勒级数展开，有

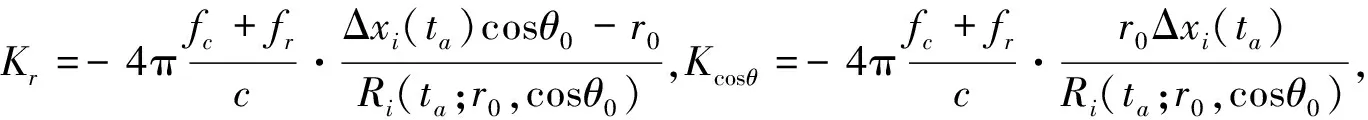
式中：Δφ(Kr,Kcosθ;r0,cosθ0)表示变量代换后的相位误差；QKcosθ、QKr分别表示Kcosθ和Kr的支撑区域。

根据式(18)，具有运动误差的图像的波数谱可表示为

I(Kr,Kcosθ;r0,cosθ0)=

exp[-j(Krr0+Kcosθcosθ0)+

jΔφ(Kr,Kcosθ;r0,cosθ0)]

(19)

文献[23]提出，当Kcosθ和Kr满足线性关系时，QPG-FFBP成像算法具备空间不变特性。

2 基于波数子带划分的SAR图像自聚焦方法

2.1 时域到波数域映射分析

根据式(10)，图像的斜距波数可表示为

SRUAV-SAR系统参数通常满足Δxi(ta)≪r0，忽略高次项近似得

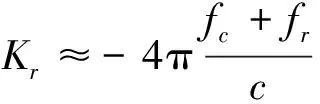
(22)

即斜距波数Kr与距离频率fr呈线性关系，具有频率相关性。在相同的方位时间，不同波数下的斜距误差和相位误差位于不同的方位波数。

由Kr/Kcosθ≈-1/Δxi(ta)得

Kcosθ≈-KrΔxi(ta)

(23)

式(23)体现了运动误差的空变特性，即不同目标在同一方位时刻的斜距误差可能位于不同的方位波数。

假设运动误差为0，无人机沿理想轨迹飞行，则式(18)可表示为

在式(24)成立的条件下，存在两个傅里叶变换对，一是斜距r和图像的斜距波数Kr，二是子孔径中心斜视角的余弦cosθ和图像的方位波数Kcosθ。利用FFT快速傅里叶变换，将FFBP成像的结果转换到方位波数域进行运动误差校正后，再逆变换回图像域得到精聚焦的图像。

实际飞行过程中，运动误差不可能为0，因此必须讨论存在误差的条件下，式(24)的成立条件，即QKcosθ和QKr。利用成像网格边缘的像素点推导约束条件[1,24]，得

式中：La为系统合成孔径长度；λ为SAR系统波长；rmin为QPG的最近斜距。对于正侧视聚束SAR，QPG的网格范围为|sinθ|≤sin(θBW/2)，其中θBW为天线的方位角度。最大值|sinθ|max=sin(θBW/2)，代入式(25)得

(26)

式(26)是式(24)的约束条件，当式(26)成立时QPG可以提供图像域(Kr和Kcosθ)与相位历程域(r和cosθ)之间的傅里叶变换关系。

2.2 NsRCM补偿

将式(19)中的运动误差引起的相位误差Δφ(Kr,Kcosθ;r0,cosθ0)沿方位向和斜距进行向量分解得

式中：Δρ(xi(ta))表示系统运动误差，是与系统的方位位置xi(ta)有关的函数；Δρr(xi(ta))和Δρcosθ(xi(ta))分别表示Δρ(xi(ta))沿斜距波数Kr和方位波数Kcosθ方向的分量。

将式(23)代入Δxi(ta)=xi(ta)-xc整理得

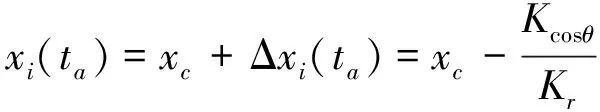
(28)

将式(28)代入式(27)得

将式(29)的两部分分别在斜距波数的中心Kr=Kr0进行泰勒级数展开，得

当下我国不动产测绘行业竞争十分激烈，这一严峻的形势使得一些资质不够的测绘机构遭到淘汰，这不仅顺应了不动产测绘市场化发展的趋势，同时对于整个行业发展而言也起到至关重要的作用。相对比其他测绘工作，不动产测绘工作要求更加严格，同时由于测绘结果对于不动产统一登记管理影响较大，所以必须要求测绘机构具备相关的资质和条件，否则不仅会对自身发展造成影响，也会使整个行业的发展造成限制。因此，不动产测绘工作的市场化发展具有必然性特点，只有在激烈的市场竞争中不断完善和发展，才能确保自身不会被淘汰，同时提高整个行业的发展水平。

(30)

式(30)中其余项都与(Kr-Kr0)有关，可归为NsRCM引起的相位误差，记作

其中

根据SAR回波数据的相干性要求，可建立方位相位误差ΔφAPE(Kr0,Kcosθ)和非系统性距离徙动ΔRNsRCM(Kr,Kcosθ)间的关系式

式(34)用方位相位误差函数ΔφAPE(Kr0,Kcosθ)及其导数表示非系统性距离徙动ΔRNsRCM(Kr,Kcosθ)，为从一个误差估计实现两个误差的估计奠定理论基础。此外，式(34)是综合考虑方位误差和斜距误差进行推导所得，可以大大简化SAR回波数据的运动误差补偿。

2.3 基于波数子带划分的SAR图像自聚焦方法流程

基于斜距波数子带划分的QPG-FFBP成像自聚焦方法流程如图3所示，共分为6个主要步骤。

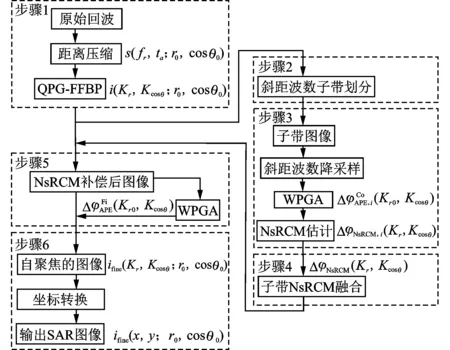
图3 算法流程图

步骤1拟极坐标系成像。使用式(14)对经过距离压缩后的原始回波数据s(fr,ta;r0,cosθ0)进行拟极坐标系FFBP成像，形成拟极坐标系下SAR图像i(r,cosθ;r0,cosθ0)。FFBP成像算法作为经典时域成像算法之一，能够对任意运动轨迹的回波数据处理生成高分辨率的SAR图像。当没有GPS和IMU等导航数据满足运动误差补偿需要时，可借助SAR回波进行运动误差补偿。由式(18)可知，图像域(Kr和Kcosθ)与相位历程域(r和cosθ)之间的傅里叶变换关系，借助IFFT将数据转换到二维波数域i(Kr,Kcosθ;r0,cosθ0)。

步骤2斜距波数子带划分。二维波数域SAR图像i(Kr,Kcosθ;r0,cosθ0)在斜距波数方向被分为几个子带信号，以克服空变的斜距波数与方位波数映射关系。每个子带信号都可近似为一个非空变的信号，同时确保具有残余RCM误差的目标能量可以落入同一个斜距单元。为了使用WPGA沿方位波数实现准确的相位误差估计，子带宽应足够小，以确保残余RCM小于一个斜距单元。子带划分后，子带图像中的相位误差可近似为非空变信号

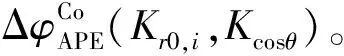
步骤4子带NsRCM融合。将每个子带估计的局部NsRCM误差ΔRNsRCM,i(Kr,Kcosθ)进行融合，得到带有空变特性的ΔRNsRCM(Kr,Kcosθ)。由式(32)可得子带NsRCM引起的相位误差ΔφNsRCM,i(Kr,Kcosθ)与NsRCM之间的关系为

NsRCM引起的总的相位误差ΔφNsRCM(Kr,Kcosθ)可以通过多个子带相位误差的加权平均来计算

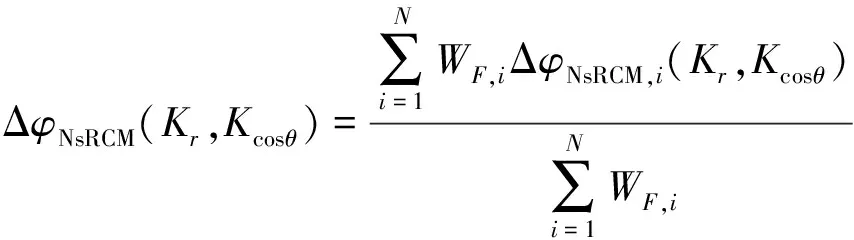
(37)

式中WF,i为加权因子。它可根据子带相位误差的方差进行计算

(38)

式中D[·]表示方差。

使用估计出的NsRCM相位误差ΔφNsRCM(Kr,Kcosθ)对图像整体进行NsRCM校正。

步骤5图像精聚焦。使用WPGA对图像进行APE估计，补偿残余APE，实现SAR图像的精聚焦，得到拟极坐标系中的精聚焦图像ifine(Kr,Kcosθ;r0,cosθ0)。由于已经补偿了NsRCM误差，因此无需再次进行降采样。

步骤6坐标转换。经过运动误差补偿和NsRCM修正后，将拟极坐标系图像ifine(Kr,Kcosθ;r0,cosθ0)投影到直角坐标系，获得聚焦良好的SAR图像ifine(x,y;r0,cosθ0)。

3 实验结果分析与验证

3.1 点目标仿真数据处理结果

点目标仿真数据的SAR参数和目标参数设置分别如表1、2所示，满足式(26)要求，即式(24)中的傅里叶变换对成立，符合PGA使用条件。仿真回波数据中添加任意形式轨迹偏差，包括距离和高度两个维度的运动误差，如图4所示。

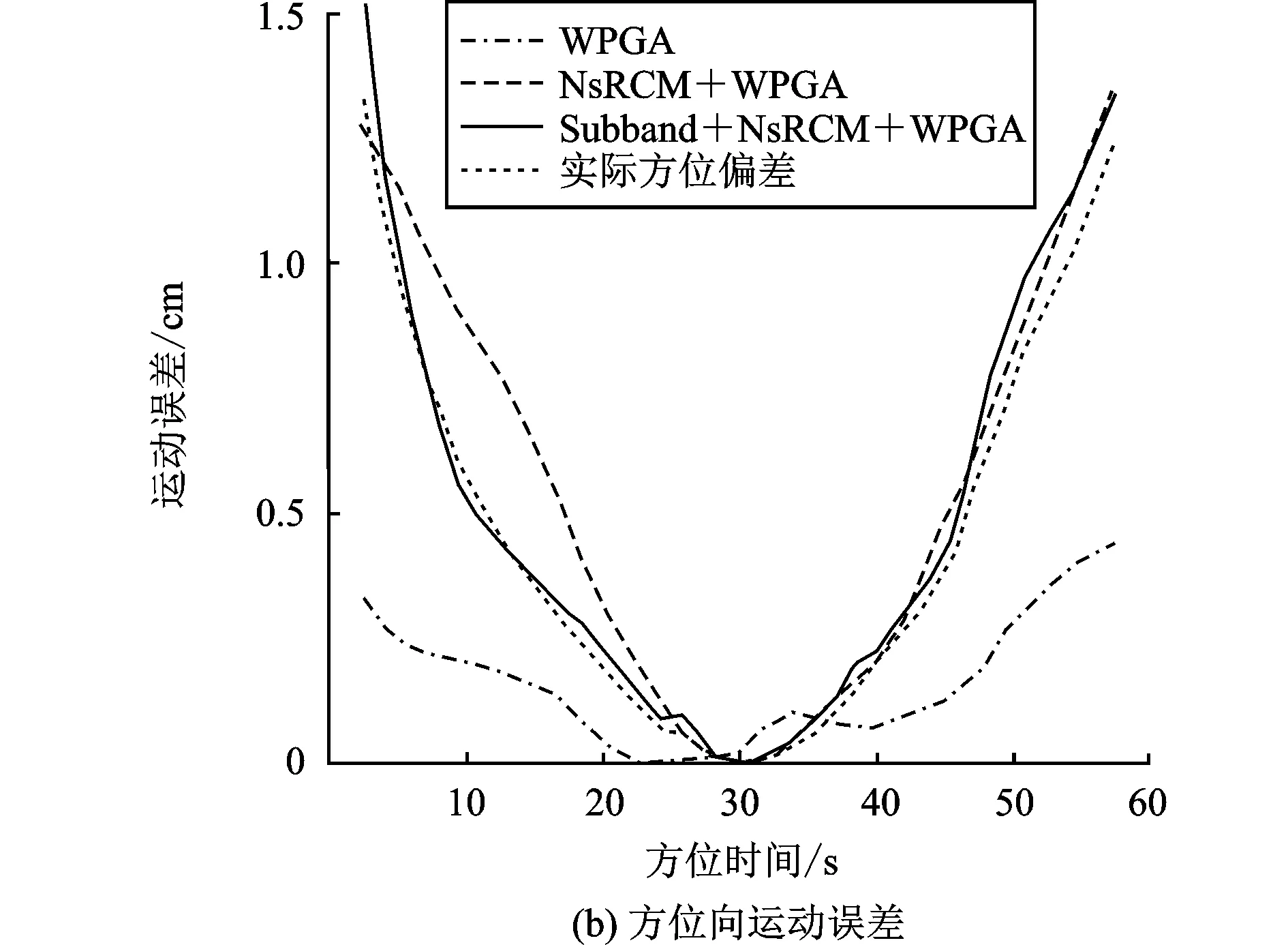
图4 运动误差结果对比

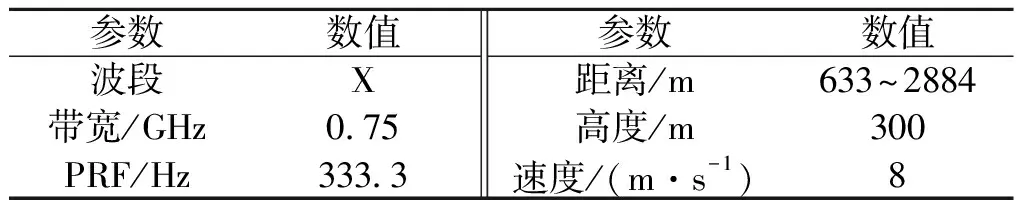
表1 系统参数

表2 9个目标点的坐标

原始回波数据经过拟极坐标系FFBP成像后(记作QPG)，选用WPGA自聚焦(记作WPGA)、文献[19]提出的运动误差补偿方法(记作NsRCM+WPGA)作为参考方法，与本文提出的斜距波数子带划分自聚焦方法(记作Subband+NsRCM+WPGA)对比，3种方法的运动误差估计结果如图4所示。由于WPGA没有NsRCM校正，故该方法没有斜距向运动误差估计结果。相较于参考方法，本文所提方法Subband+NsRCM+WPGA具有最佳的估计精度。

仿真点目标数据成像结果如图5所示，图中彩色曲线为拟极坐标系中非线性采样导致的方位坐标弯曲，故相同方位坐标不同斜距的目标在图中的位置并不在一条直线上。取中心点A和边缘点B局部放大。

由于轨迹偏差的存在，图5(a、b、c)存在严重散焦；WPGA自聚焦处理和NsRCM+WPGA处理虽然可以对场景中心点A进行聚焦，但场景边缘点B仍存在散焦；Subband+NsRCM+WPGA处理能同时提升场景中心点A和边缘点B的聚焦效果。图5的中心点A和边缘点B方位向和斜距向剖面图如图6所示，本文所提方法可明显提升方位向和斜距向的分辨率和峰值旁瓣比，尤其是边缘点B的方位向性能。

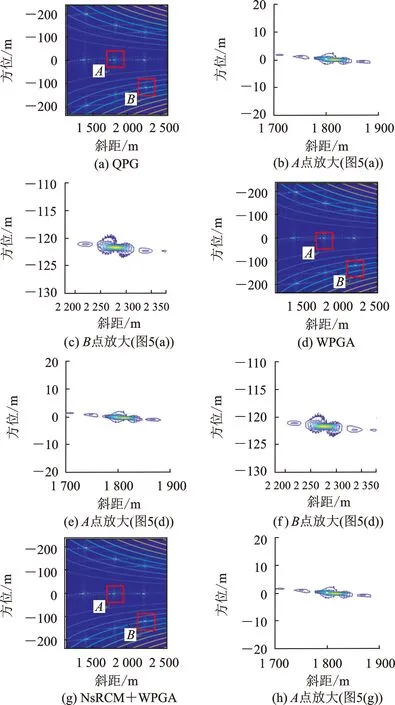
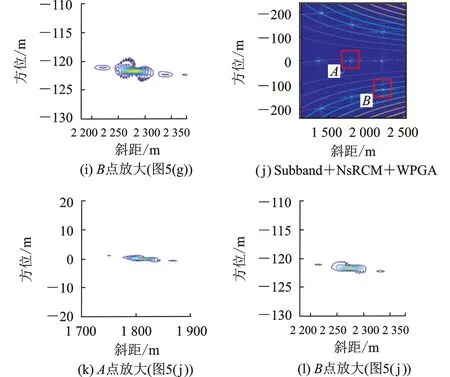
图5 仿真点目标成像结果

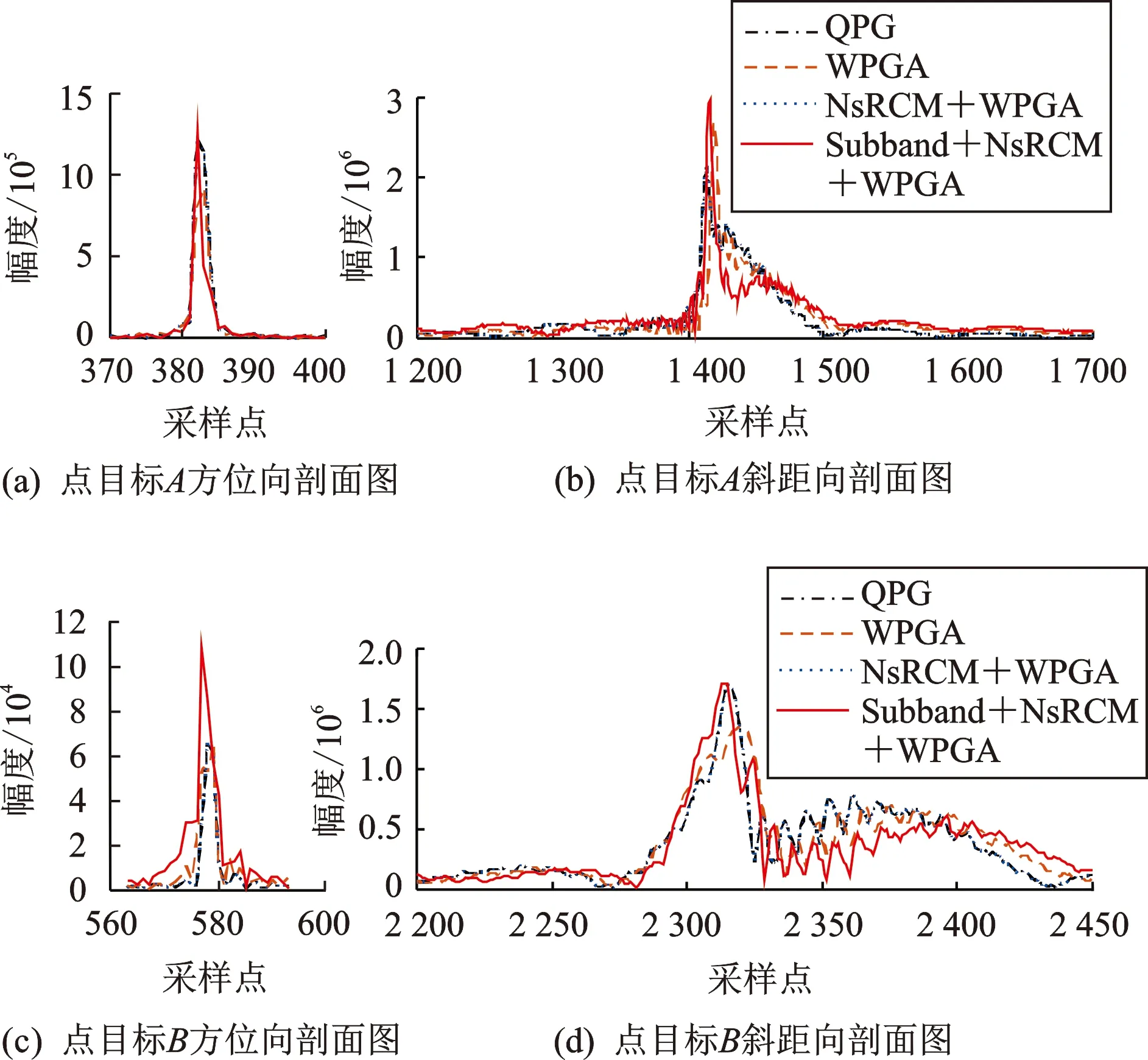
图6 点目标A、B性能

3.2 实测数据处理结果

2021年9月，在中国石家庄长安区收集了基于小型旋翼无人机的SAR实验数据，系统工作参数见表1。选取采集数据的合成孔径时间约为60 s。场景为滹沱河高尔夫球场，光学图像如图7(a)所示。由于机载GPS和INS精度较低，无法满足运动误差补偿需要，故采用接收的回波来估计运动误差。

由于系统带宽为0.75 GHz，将图像在斜距波数域分为0.3 GHz的子带，确保每个子带与相邻子带有一定重叠。所用方法与仿真数据处理方法相同，处理结果如图7(b)所示。将图像中场景A和场景B局部放大，选取特征点，自聚焦成像方法效果对比如图8所示。图8(c—f)是图8(a)中点C的局部放大，可见由于未知的平台运动轨迹偏差，只用拟极坐标系下FFBP成像，图8(c)图像存在散焦；通过WPGA自聚焦处理后，受运动误差空变性的影响，图8(d)仍存在散焦；NsRCM+WPGA处理后，同样受运动误差空变性影响，图8(e)也存在散焦；采用Subband+NsRCM+WPGA方法自动聚焦，图8(f)方位向和斜距向的主瓣能量得到增强，聚焦效果得到提升。图8(g—j)是图8(b)中点D的局部放大，相较于图8(g—i)，图8(j)的目标主瓣能量更强，方位向分辨更清晰，聚焦效果最好。分别计算各方法处理后C点和D点的峰值旁瓣比(peak sidelobe ratio, PSLR)和积分旁瓣比(integrated sidelobe ratio, ISLR)，如表3所示，进一步验证了本文所提方法的有效性。

图7 场景图像

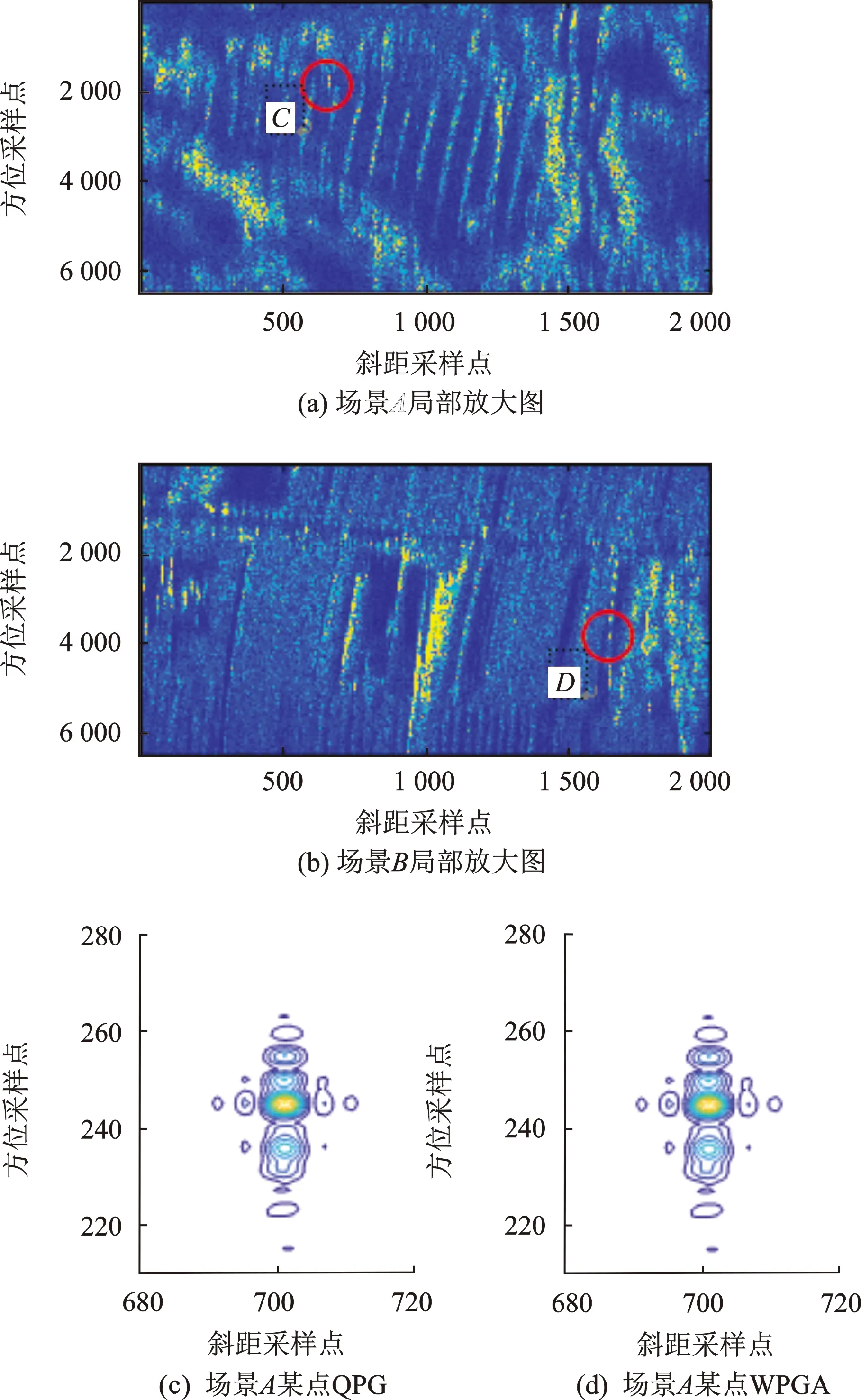
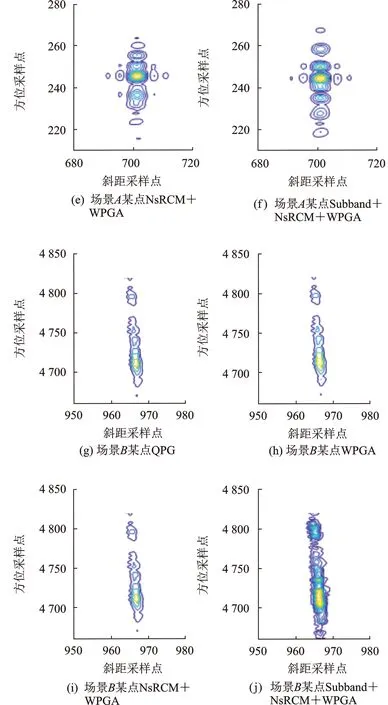
图8 拟极坐标系场景局部图像

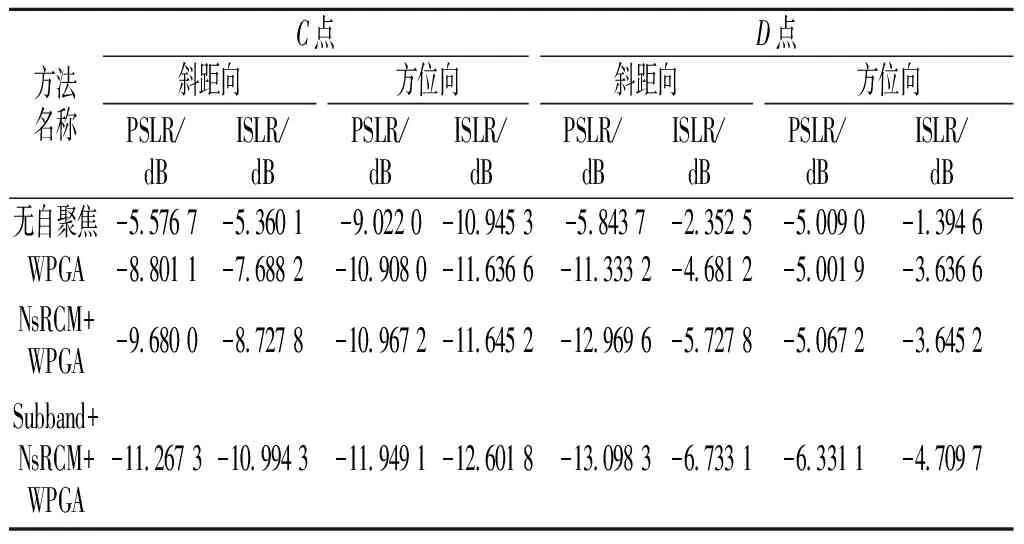
表3 图8中C点和D点性能参数表

4 结论

本文针对小型旋翼无人机平台的运动特点，提出了一种基于斜距波数子带划分的SAR成像自聚焦方法，该方法能在不限制斜视角的情况下完成SAR成像；采用斜距波数多子带划分和融合来适应运动误差的二维空变特性；利用APE和NsRCM误差的相干性，通过两次WPGA估计分别校正NsRCM和APE误差。经仿真和实测数据处理验证，该方法真实有效，适用于无高精度INS的小型旋翼无人机载SAR自聚焦成像。