一种链式多体系统接点约束力的求解方法
2022-06-29刘俊谊谢兴坤
刘俊谊, 谢兴坤, 洪 娟, 黄 恒, 计 淞
(陆军工程大学 野战工程学院,江苏 南京 210007)
作为当今力学领域的研究热点和难点之一,多体系统动力学为航空航天、兵器、机械、机器人和近海工程等领域中相关系统的动态性能评估和优化设计提供了重要的理论基础和技术支撑[1-3]。20世纪70年代,Wittenburg[4]出版了第一本多体系统动力学专著,利用图论方法奠定了多刚体系统动力学拉格朗日(Lagrange)方法的基础。之后,Schichlen[5]基于有限元系统和连续系统相互等价的假定,提出了Schichlen方法。Kane等[6]建立了兼有矢量力学和分析力学优点的凯恩(Kane)方法,并研究了该方法在航天器动力学上的应用。在此基础上,Huston[7]提出了适于数值计算的Kane-Huston方法。该方法采用低序体阵列描述多体系统的拓扑结构,利用欧拉(Euler)参数描述系统物体间的相对方位,避免了数值计算过程的奇异性困难。
Kane方程的形式较为简单,非常适合创建复杂系统的动力学模型,因此很多学者将其应用于空间机械臂[8]、机器人[9]及近海工程结构物[10]等的动态响应问题研究。Yang等[11-12]基于Kane动力学方程分别建立了水下蛇形机器人和水下四足行走机器人的动力学模型,并对它们的运动响应进行了数值分析。杜晓旭等[13]利用Kane方法建立了波浪驱动的水下航行器动力学方程,研究了缆索长度和航行深度对系统运动的影响。通过将缆索简化为一系列具有不同物理特性的相互铰接的刚性杆,李晓平等[14-15]基于Kane方法建立了水下拖曳柔索系统的三维有限段模型,并利用模型试验验证了计算模型的合理性。王磊等[16]将Kane方法与模态叠加法相结合,建立了陆上风电机组整机刚柔耦合结构动力学模型。此外,Liu等[17]利用Kane方法对走锚消能式拦阻系统受船舶撞击后的动态响应进行了研究,并通过多体系统动力学软件机械系统动力学自动分析(automatic dynamic analysis of mechanical systems,ADAMS)验证了所建立的多体动力学模型的有效性及开发程序的可信性。
目前,基于Kane方法所开展的多体系统动力学分析中,主要侧重于系统中各物体本身的运动和动力响应的求解,而对于物体间的接点约束力的研究相对较少。对此,本文以链式多体系统为研究对象,基于Kane方法建立其动力特性分析的数值计算模型,给出其接点约束力的求解方法,并通过与多体系统离散时间传递矩阵法和经典力学方法相关结果的对比分析,验证所建模型的合理性和有效性。
1 链式多体系统动力特性分析的数学模型
Kane方法兼有矢量力学与分析力学的优点,Huston方法是Kane方法在多刚体系统中的具体应用,它采用了独创的低序体阵列描述多体系统结构,并引入了偏速度、偏角速度、广义速率和广义力等概念。运用Huston方法进行多体系统动力学分析的核心是计算由偏速度、偏角速度及广义速率等表达的广义惯性力和广义主动力,进而建立Kane方程并进行求解。下面按照Kane-Huston方法[7]的基本思想,建立链式多体系统动力特性分析的数学模型。
1.1 坐标系的建立及坐标转换矩阵
首先,对链式多体系统(N级摆)中的各物体进行编号并建立如图1所示坐标系,与固定端o0相连的杆件记为B1,然后沿其连接方向依次编号为B2,…,BN。惯性系的原点位于系统的固定端o0处,x0轴水平向右,z0轴竖直向上,y0轴与x0轴、z0轴满足右手定则。刚体Bk与其内接刚体(邻接较低序号的刚体)的铰接点即是Bk的连体坐标系原点ok,xk轴沿杆件方向,yk轴与y0轴方向相同,zk轴与xk轴、yk轴同样满足右手定则。图中θk表示刚体Bk与x0轴正向的夹角。
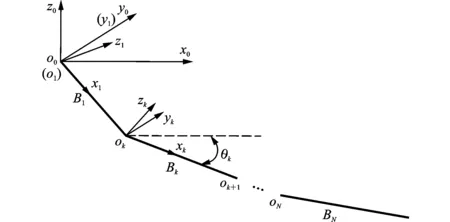
图1 链式多体系统示意图
物体偏速度、偏角速度的计算与坐标系间的变换矩阵密切相关。因此,首先需要明确变换矩阵的相关计算。当使用刚体Bk相对其内接刚体Bj运动的卡尔丹角αk、βk、γk描述刚体姿态时,刚体Bk相对其内接刚体Bj的坐标变换矩阵可写为
式中:C表示余弦运算cos,S表示正弦运算sin。为了避免使用卡尔丹角进行数值计算时可能遇到的奇异性问题,采用欧拉参数描述刚体转动。由变换矩阵求解欧拉参数εki(i=1,2,3,4)的公式为
S(jk)可用欧拉参数εki(i=1,2,3,4)写为
初始时刻,各物体间的夹角已知,因而可以通过式(1)求得变换矩阵S(jk)。然后,可以利用式(2)求解此时刻相应的欧拉参数,之后的数值计算中,每一时刻的欧拉参数均可通过求解式(4)的一阶微分方程得到。
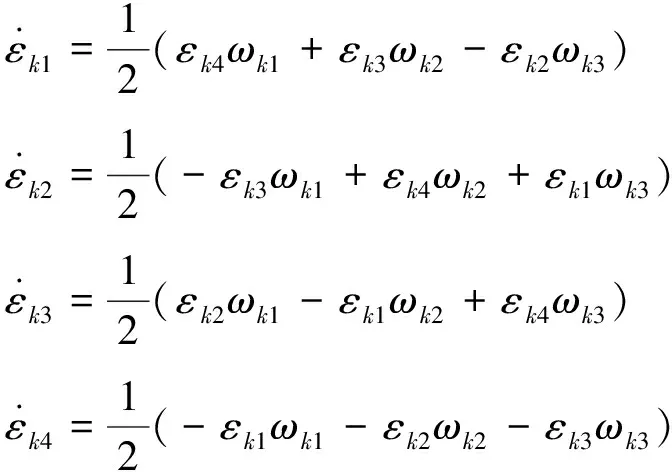
(4)
式中:ωk1、ωk2、ωk3为刚体Bk相对其内接刚体的角速度分量。将欧拉参数的计算结果代入式(3)即可得到相应的刚体间变换矩阵。刚体Bk相对惯性坐标系的变换矩阵S(0k)可由Bk至零刚体(惯性系)通路上各对连接刚体间的变换矩阵连乘得到,即
v=Lt(k),w=Lt+1(k),Lu(k)=1
(5)
L(k)为邻接较低序号算子,在此基础上求解刚体Bk相对于惯性系转动运动响应的公式为
式中:α(0k)、β(0k)、γ(0k)分别为刚体Bk相对惯性系运动的卡尔丹角。
变换矩阵的导数可通过矩阵的乘积表示为

(7)
式中:W(0k)为刚体Bk角速度ω(0k)的对偶矩阵。其表达式为
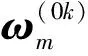
i,r,m=1,2,3
(9)
1.2 广义速率和广义坐标
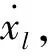
(10)
1.3 偏速度、偏角速度阵列及其导数
点的速度和体的角速度可表示为广义坐标导数的线性函数组合,这些导数的系数称为“偏速度”和“偏角速度”。刚体Bk在惯性参考系中的绝对角速度ω(0k)可用偏角速度表示为
k=1,2,…,N;l=1,2,…,6N;m=1,2,3
(11)
式中:m、l为哑标;n0m为惯性坐标系的矢量基。根据广义速率的定义,偏角速度ωklm的表达式为
式中δm,l表示Kronecker’s delta函数
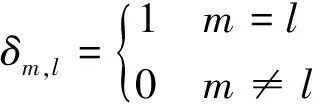
(13)
如图2所示,令ok为刚体Bk连体坐标系的原点,Qk为刚体Bk与其内接刚体Bj的连接点并固定在Bj上。矢量qk给定连接点Qk与原点oj(j=L(k))的相对位置,用刚体Bj的连体坐标系表示。矢量sk表示原点ok与连接点Qk的相对位置,描述刚体Bk相对其内接刚体Bj的移动,用刚体Bj的连体坐标系表示。矢量rk给定质心Ck与原点ok的相对位置,用刚体Bk的连体坐标系表示。

图2 通路上的物体和相关矢量
同理,刚体Bk的绝对速度v(0k)可用偏速度表示为
k=1,2,…,N;l=1,2,…,6N;m=1,2,3
(15)
偏速度分量vklm的表达式为
式中:qvn和svn分别为通路上连接点矢量qv和相对位移矢量sv在Bv内接刚体连体坐标系中的投影值;rkn为rk在刚体Bk连体坐标系中的投影值。
v=Lt(k),w=Lt+1(k),Lu(k)=1,
l=1,2,…,3k;k=1,2,…,N;t,h,m=1,2,3
l=3k+1,3k+2,…,3N;k=1,2,…,N
l=3N+1,3N+2,…,6N;k=1,2,…,N
(17)
1.4 链式多体系统的凯恩方程
通过前面的分析可以发现:任意刚体Bk质心的速度v(0k)和加速度ak以及Bk的角速度ω(0k)和角加速度αk可用偏速度和偏角速度阵列及其导数表示为
若刚体Bk对于原点位于其质心处连体坐标系的惯量矩阵为[ICk],则Bk相对于惯性参考系的惯量矩阵为
[Ik]=[S(0k)]T[ICk][S(0k)]
(19)
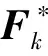
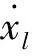

(21)
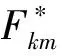
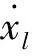
Fl=vklmFkm+ωklmTkm
l=1,2,…,6N;k=1,2,…,N;m=1,2,3
(23)
系统内部光滑铰和光滑面接触等理想约束成对出现,其约束力对广义主动力的贡献为零,因而可不予考虑。
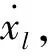

(24)
将广义力的表达式代入式(24),同时考虑到链式多体系统物体间无相对移动,化简后可得到链式多体系统的基本运动力学方程
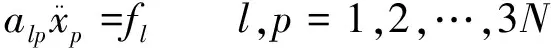
(25)
式中的系数为
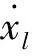
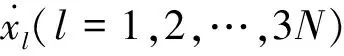
2 接点约束力的求解方法
根据上述的Huston方法,可以求得每一时刻每个物体相对静止坐标系的运动响应,包括角速度、角加速度、速度、加速度等物理量,然而,计算广义主动力时并没有考虑光滑铰处的约束力,因此若要确定它们的大小则需进一步地分析计算。下面分别基于Kane方法和经典力学的方法对其进行分析。
2.1 基于Kane方法求解
首先,根据前面分析中已经消去的方程计算广义约束力(作用于各刚体质心处约束力主矢和主矩的广义力)。其过程如下:
将接点约束暂时去掉,而保留约束力和力矩分量,且视之为外部作用的力和力矩。系统将具有与被去掉的约束相应的增加的自由度,也就出现了与这些增加的自由度相应的增加的动力学方程(即原来被消去的那些方程)。待求的广义约束力将出现在这些方程中,而且,由于采用体间的相对角速度分量或相对位移速率作为广义速率,广义约束力将在这些方程中单独(无耦合)出现。即在每个方程中将仅有广义约束力的1个分量(如用方位角导数作为广义速率,将不是这种情况)。将已知的广义速率和广义坐标代入这些方程,则各方程即成为求解广义约束力的解耦的代数方程。
链式多体系统中,暂时去掉接点约束可得方程为
l=3N+1,3N+2,…,6N;p=1,2,…,3N
(27)
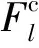
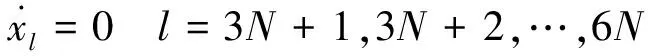
(28)
由于假定链式多体系统中的铰链均为光滑铰,所以铰链处只有约束力而不存在约束力矩(阻尼力矩)的作用。因此,系统的广义约束力为
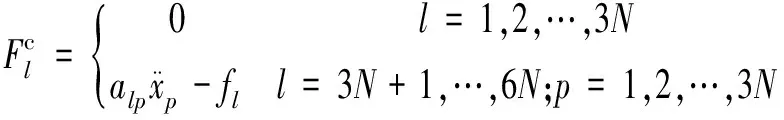
(29)

l=1,2,…,6N;k=1,2,…,N;m=1,2,3
(30)

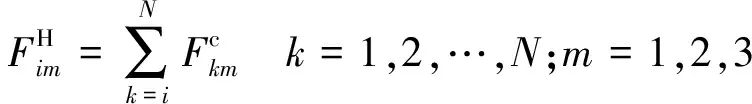
(31)
2.2 基于经典力学的方法求解
对链式多体系统中任意刚体Bk进行力学分析如图3所示。
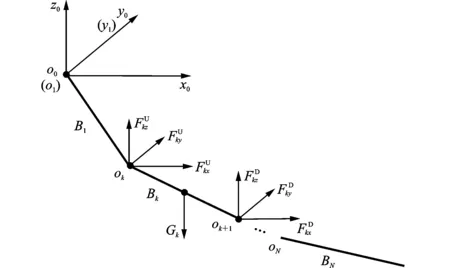
图3 N级摆系统内杆件受力示意图
根据牛顿第二定律和第三定律可得
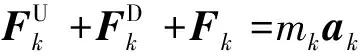
(32)

(33)
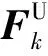

3 算例分析
3.1 参数选择
取N级摆节数N=3;重力加速度g=9.81 m/s2;积分时间步长Δt=0.001 s;积分时长t=10 s;各杆件长度l=1 m;半径R=0.1 m;质量m=1 kg;由于各杆件为均质杆件,根据上述对连接矢量的定义,q1=[0,0,0]T、qk=[l,0,0]T(k=2,3,…,N)、rk=[l/2,0,0]T(k=1,2,…,N)。初始时刻各杆件静止且与x0轴正向夹角均为-π/3,各摆仅在x0o0z0平面内运动,则有αk=γk=0(k=1,2,3)、β1=π/3,β2=β3=0;各杆件在以其质心为原点的连体坐标系中的惯量矩阵为

(34)
3.2 结果分析
选取参数后,按照Huston方法的求解过程编程计算,即可得到系统内各摆的运动响应。下面首先确立数值计算的有效性,基于能量守恒原理的验证及与多体系统离散时间传递矩阵法计算结果[18]的对比分别如图4和图5所示。
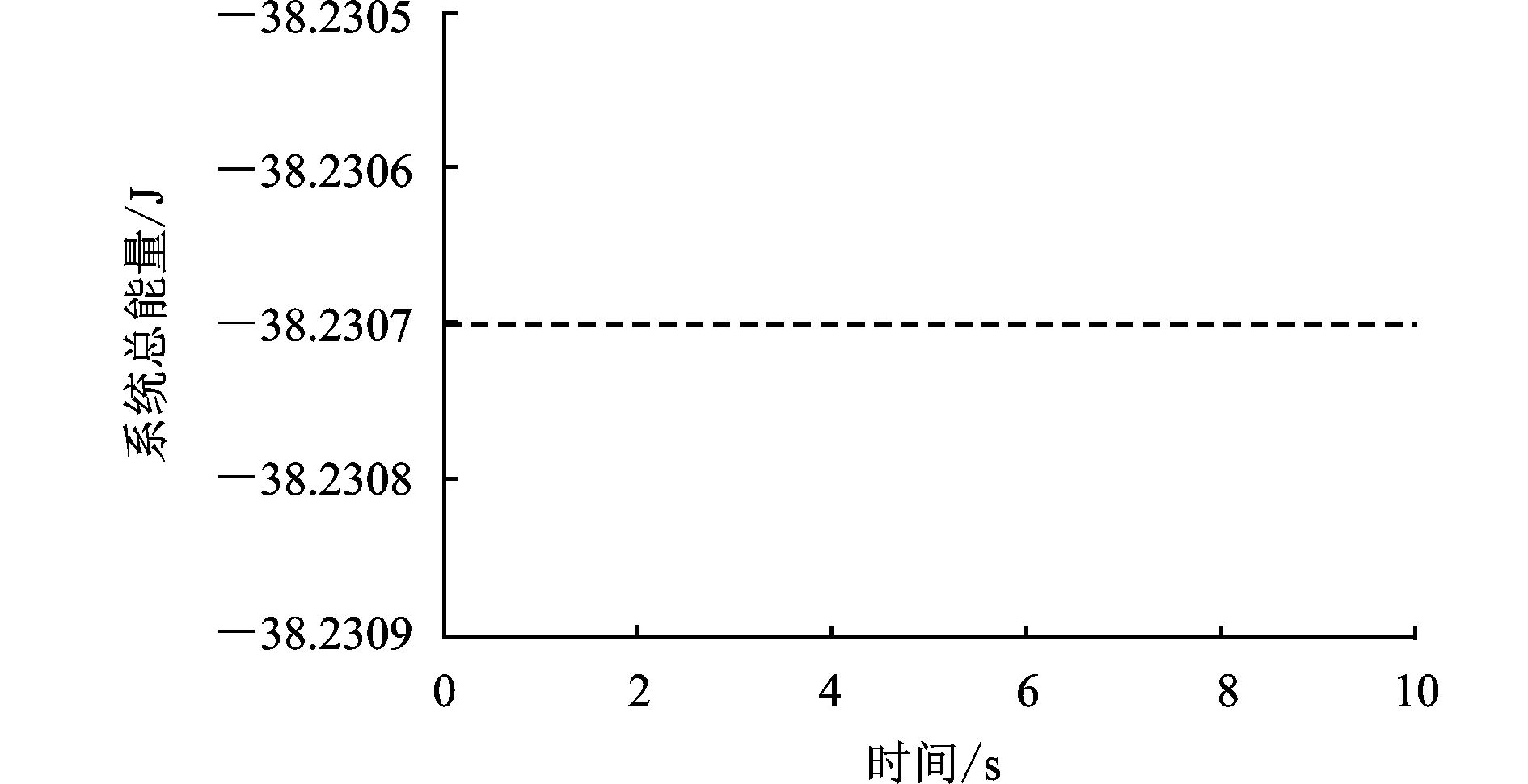
图4 能量守恒原理对平面三级摆系统数值仿真精确性的验证
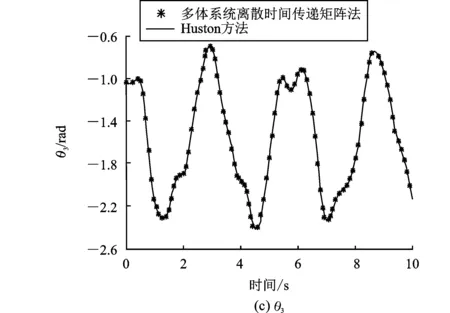
图5 平面三级摆的角位移计算结果
对比表明,两种方法的计算结果一致性很好,说明了Huston方法解决多刚体动力学问题的有效性及数值计算的可信性。对两种确定多体系统内约束力的方法进行比较,结果分别如图6和图7所示。
观察图6和图7可以发现:两种方法计算接点约束力的结果十分吻合,相互验证了它们各自的有效性和准确性。两种方法的效率和精度均基本一致,但从计算便捷性的角度看,Kane方法略有优势,因为其不需要对每个物体进行单独的受力分析。
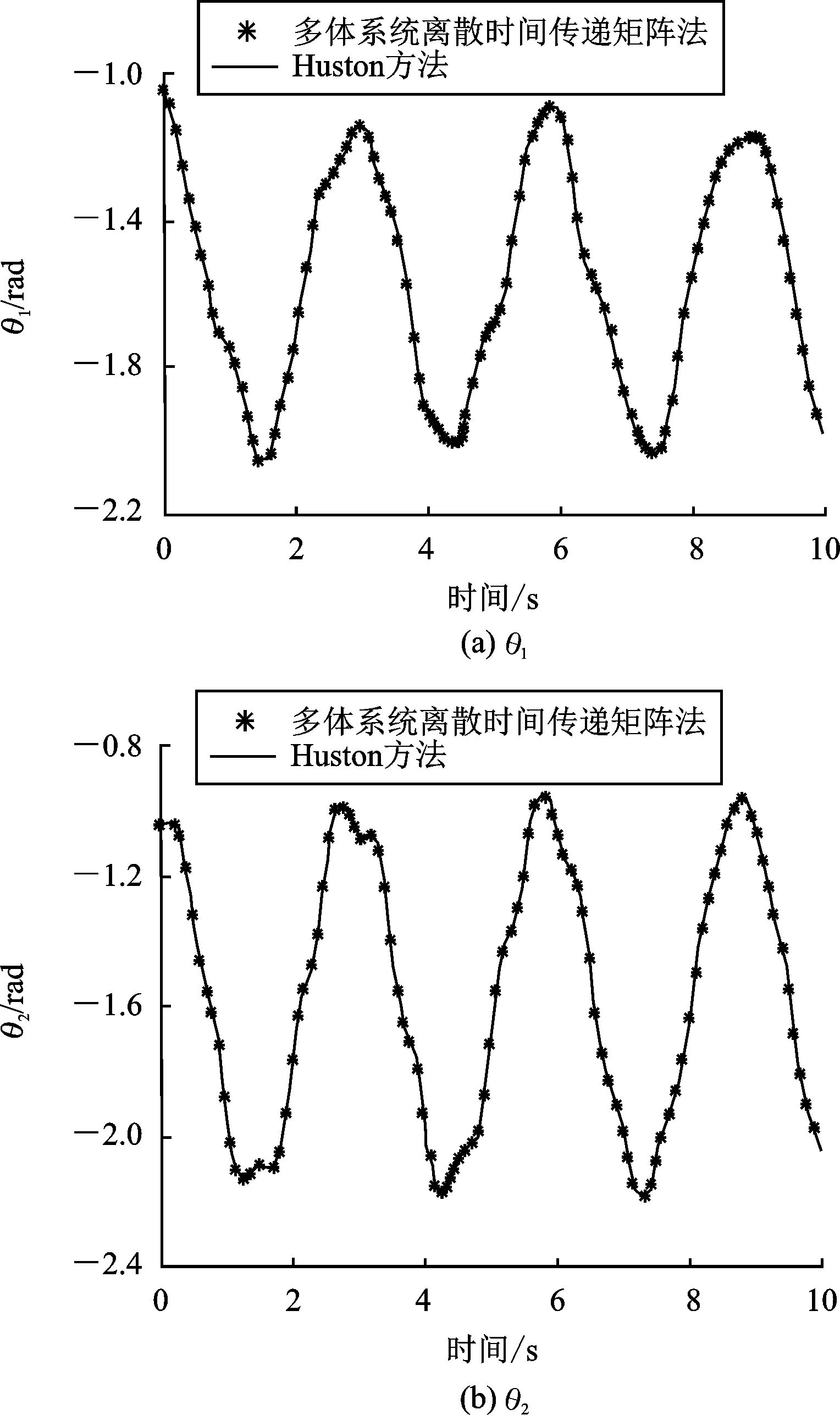

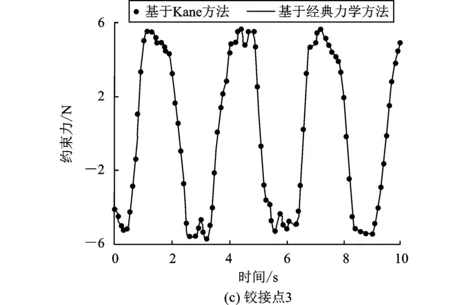
图6 平面三级摆各铰接点x方向约束力
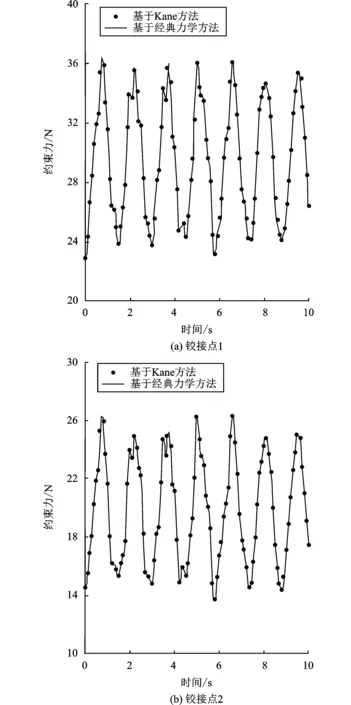

图7 平面三级摆各铰接点z方向约束力
4 结论
本文首先运用Kane-Huston方法对链式多体系统的运动响应进行了建模,并提出两种确定系统内(铰)接点约束力方法。然后,以三级摆为算例对多体系统的运动响应及(铰)接点约束力进行了求解。通过能量守恒原理及与文献[18]中的计算结果对比验证了Huston方法数值计算的有效性,进而将基于Kane方法和经典力学方法求解(铰)接点约束力的结果对比,验证了两种方法的有效性和准确性。
本文所建模型及相关结果对利用Kane方法开展多体系统动力学分析具有一定的参考意义。但同时,本文的研究也存在一些不足。例如,算例中的铰链假定为光滑铰、系统内各物体假定无初速度且不受除重力以外的外力作用。进一步针对更为复杂的工况条件开展链式多体系统动力学分析具有重要的工程实践意义。
