弹载自测速修正的炸点控制技术

石永雷， 房立清， 郭德卿， 谢高杨， 齐子元， 杨玉良

(1.陆军工程大学 石家庄校区，河北 石家庄 050003；2.河北科技大学 机械工程学院，河北 石家庄 050018)

现代的战场环境复杂多变，在波谲云诡的战场环境下对锁定的军事目标实现精确的打击是武器系统提高作战效率的有力保证。装有定距空炸引信的弹药不仅可以对既定的军事目标实现精确的打击，也可以使弹药从杀伤有生点目标转变为杀伤有生面目标来提高杀伤效果。因而炸点精确控制技术在现代战争中具有较高的军事意义。目前常用的定距空炸的方法有计时、计转数以及计时计转数复合炸点控制技术[1]。电子时间引信具有结构简单、可靠性较高的特点而广泛应用于武器系统。

电子时间引信的定距精度受制于诸多因素，其中炮口初速度是影响弹丸飞行特征的最主要参数[2]。大量的实践表明弹丸炮口初速具有一定的散布性，这是由于每发弹的装药量略有不同以及弹道枪在每发弹发射过程中的后坐力也不尽相同等因素导致[3-4]。在空炸距离一定时不同的初速下引信的作用时间不同，因此必须实时地测量每发弹的初速[5]。

目前测量炮口初速的方法有很多种，文献[6～8]提出的激光测速、天幕靶测速以及雷达测速可以达到较高的测量精度，但测速结果需要通过无线装定的方式实时装定到弹丸中。无线装定需要复杂的发射平台而且受外部不可控因素影响较多，因而装定效果有时并不理想。弹载自测速可以同时实现测量和装定的双重功能并且可以降低测量平台的复杂性，提高弹丸初速测量的可靠性。文献[9]提出了一种通过计转数的方式实现弹载自测速，但该方法可能受电磁干扰使转数信号紊乱，严重时可能会导致测速失败[9]。基于线圈靶进行弹载自测速的方法受电磁干扰较少而且结构简单不需要复杂的发射平台[10-11]。该种弹载自测速方法只需在炮口上架设相距一定距离的激励线圈[12-14]。为了提高测速的精度和可靠性，本文针对该种弹载自测速的实现方法以及关键技术进行分析。

针对电子时间引信的时间修正方法，文献[15]根据射程相等原则提出一种反比例修正法。文献[16]通过探究引信作用时间变化量与海拔高度变化关系，通过推算不同射程下的海拔修正系数实现对引信装定时间的修正而提高了弹丸定距精度。文献[17]和文献[18]着重分析了基于计转数弹载测速的自修正技术，通过理论仿真和靶场动态试验取得了一定效果。

时间修正方法中的反比例修正法认为弹丸的弹道具有相似性，假设理论弹道与实际弹道在对应点速度的比值和方向是相同的。因而反比例修正法是一种简化的修正方法，其忽略了不同初速下弹丸飞行轨迹不同以及飞行过程速度衰减情况。一次函数修正法不用考虑弹丸实际弹道与理论仿真弹道上相同点速度的比值与方向，因而可以避免理论假设带来的缺陷，可满足工程应用中的精度要求[19]。

1 系统组成结构

自测速修正炸点控制系统主要由信号处理模块、计时模块、解算模块、存储模块、控制模块以及供电模块构成。信号处理模块由弹丸内部的感应线圈以及外围信号处理电路构成。微处理器的A/D模块实时地采集弹丸内部感应线圈的电压信号，当感应电压信号达到规定的阈值后由计时模块负责开始或者停止计时。解算模块可解算弹丸穿过外部激励线圈的飞行时间并根据飞行时间解算出弹丸的飞行速度。存储模块负责存储系统的程序、弹丸的飞行时间、线圈距离值、弹丸的初速值以及修正后引信作用时间。当弹丸飞行至预定的时间节点后控制模块发出相应的控制信号来引爆弹丸。供电模块为微处理器以及各个模块提供电能。炸点控制系统的组成结构图如图1所示。

图1 自测速修正炸点控制系统组成结构

2 弹载自测速原理及关键技术分析

弹载自测速方法是一种非接触式被动测速方法[10-14]，其主要通过区截法测速。测速的基本工作原理如下：

(1) 弹载测速系统高速穿过相距一定距离的两个激励线圈时弹丸上的感应线圈会产生感应电压信号并实时由微处理器采集。

(2) 感应电压上升到规定的阈值时微处理器启动计时或停止计时。结合激励线圈的距离和弹丸飞行时间，通过微处理器内置的程序解算出弹丸在这段时间内的平均速度。

(3) 两个线圈的距离较短且弹丸飞行速度较快，因此可以把平均速度作为弹丸出炮口的速度。图2为炮口初速测量装置示意图，其中1和2是激励线圈，3为炮口制退器。值得注意的是两个线圈的安装要错开后效期位置并进行相应的修正。

我是一个重感情的人，虽然在这边工作很顺心，但我时常会想念冯阿姨，想起她和蔼的面容，想起她关切的话语，想起我们在一起的点点滴滴。终于我拿起手机拨通了她的电话，原想有好多话跟她说，但当电话那头传来：“小刘，你在那边干得还好吗？”我反倒一句话也说不出来了，眼泪顿时模糊了我的眼睛，有些东西当我们真正拥有的时候也许并不能感觉到它存在的重要性，不懂得珍惜，直到离开了才会去怀念曾经的生活。

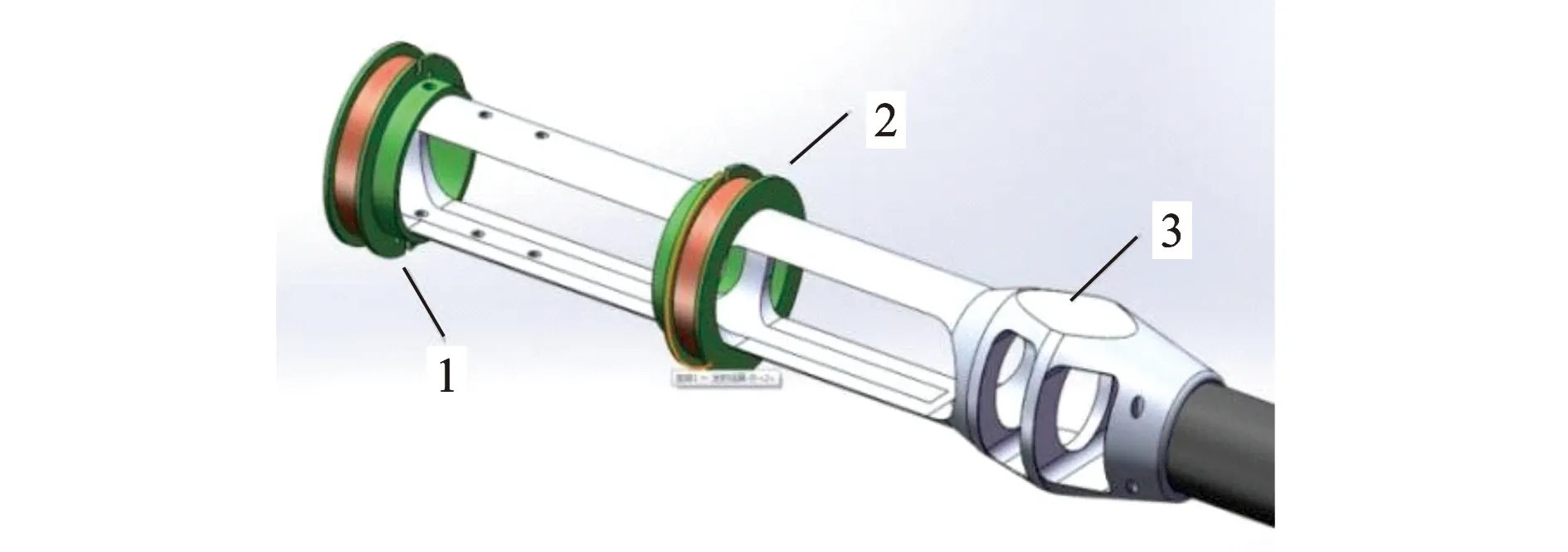
图2 炮口初速测量装置示意图

2.1 感应电压信号波形分析

根据毕奥-萨伐尔定律，通电圆环轴线上某点的磁感应强度B的大小为

(1)

式中：μ0为真空磁导率，N0为线圈匝数，I为通电电流，R为磁环半径，X为轴线上某点的坐标。通过方程(1)可得到激励线圈沿轴线的磁场分布情况。由法拉第电磁感应定律可知感应电压信号为

式中：N1为感应线圈的匝数，v为弹丸速度，S为感应线圈面积。把相关参数代入式(2)并用MATLAB绘制感应电压信号如图3所示。实验过程中使感应线圈快速穿过激励线圈并用示波器捕捉电压信号波形如图4所示。

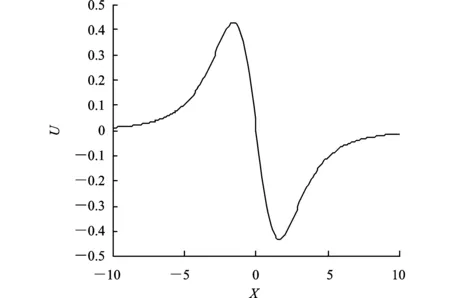
图3 感应电压信号的仿真

从图3和图4可知，通过MATLAB仿真和示波器捕捉的感应电压信号都有类似“正弦函数”的波形。感应电压信号的特点是上升过程较为缓慢，而从峰值下降的过程很快。对于均匀缠绕的激励线圈，其几何中心与其电磁中心是相重合的。由激励线圈轴向磁场分布的表达式可知，激励线圈几何中心处的磁场强度最大。由感应电压波形可知，感应电压为0的点处曲线斜率很大，且为激励线圈的几何中心。因此选择靠近感应电压为0处附近的点进行触发计时，这有利于减少测速误差。

图4 示波器捕捉的感应电压信号

2.2 激励线圈距离的确定

激励线圈间的距离变化将会导致线圈间磁场的变化，这进一步会影响弹丸穿过激励线圈时的感应电压。以两激励线圈轴线上的中点为坐标原点建立轴向磁场分布的数学模型

式中L为两线圈的距离。同样利用电磁感应定律可得到感应线圈上电压变化规律为

(4)

通过线圈的距离L与线圈的半径R之间的关系来探究感应电压的变化规律。图5仿真了两激励线圈不同距离时感应电压的变化规律(横纵坐标不代表真实值，这并不影响电压变化规律)。从图5可以看到，当激励线圈间的距离小于半径时感应电压只出现一个峰值，此时微处理器无法感应到两次脉冲信号使计时器开始或者停止计时。随着线圈距离的不断增大，感应线圈穿过两个激励线圈时的电压波形越独立。当激励线圈距离为其半径的2.5倍时呈现了两个较为独立的电压波形，这表示线圈间的距离对感应电压的影响较小。参照仿真结果通常设置激励线圈距离为其半径的3～5倍。

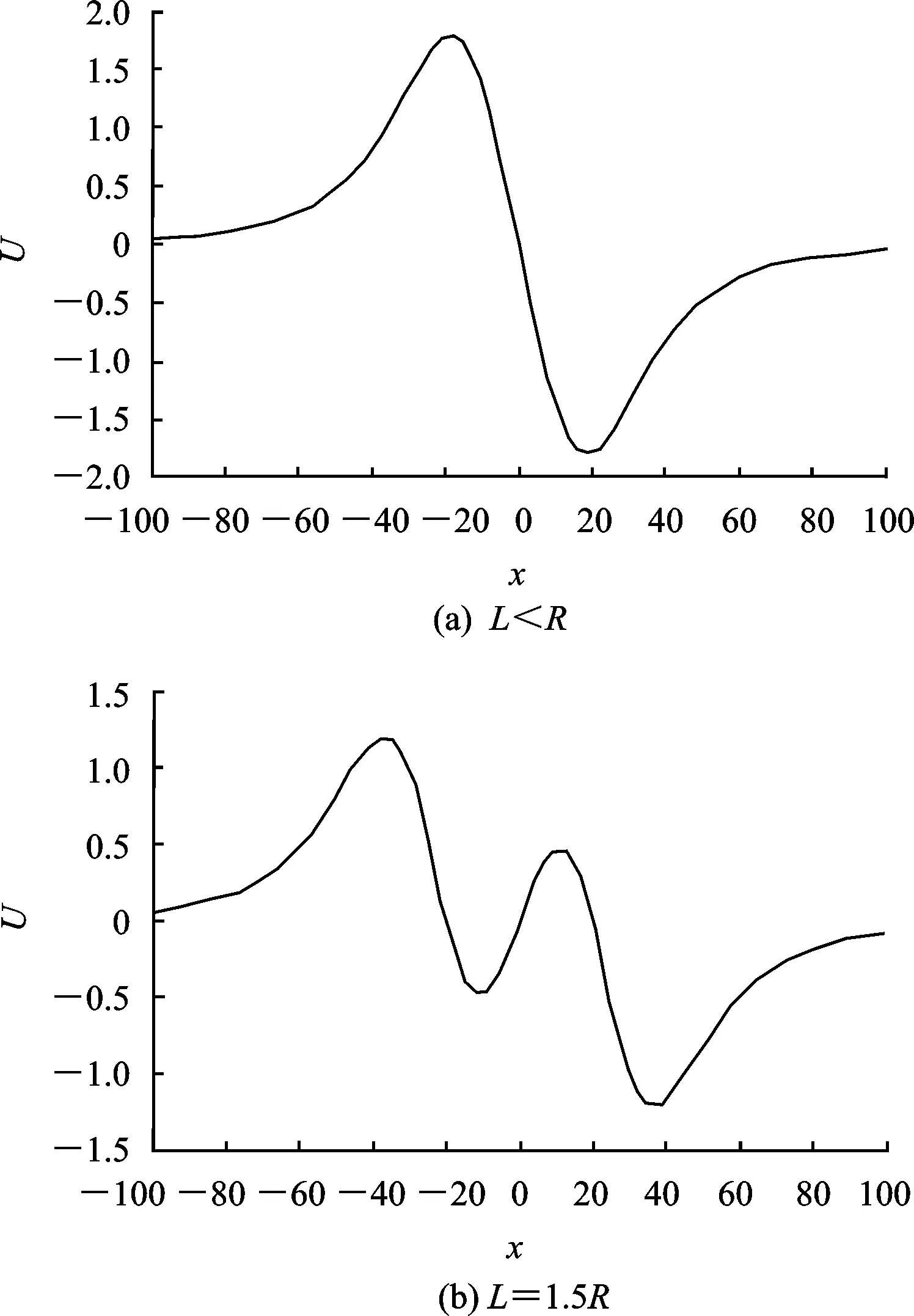
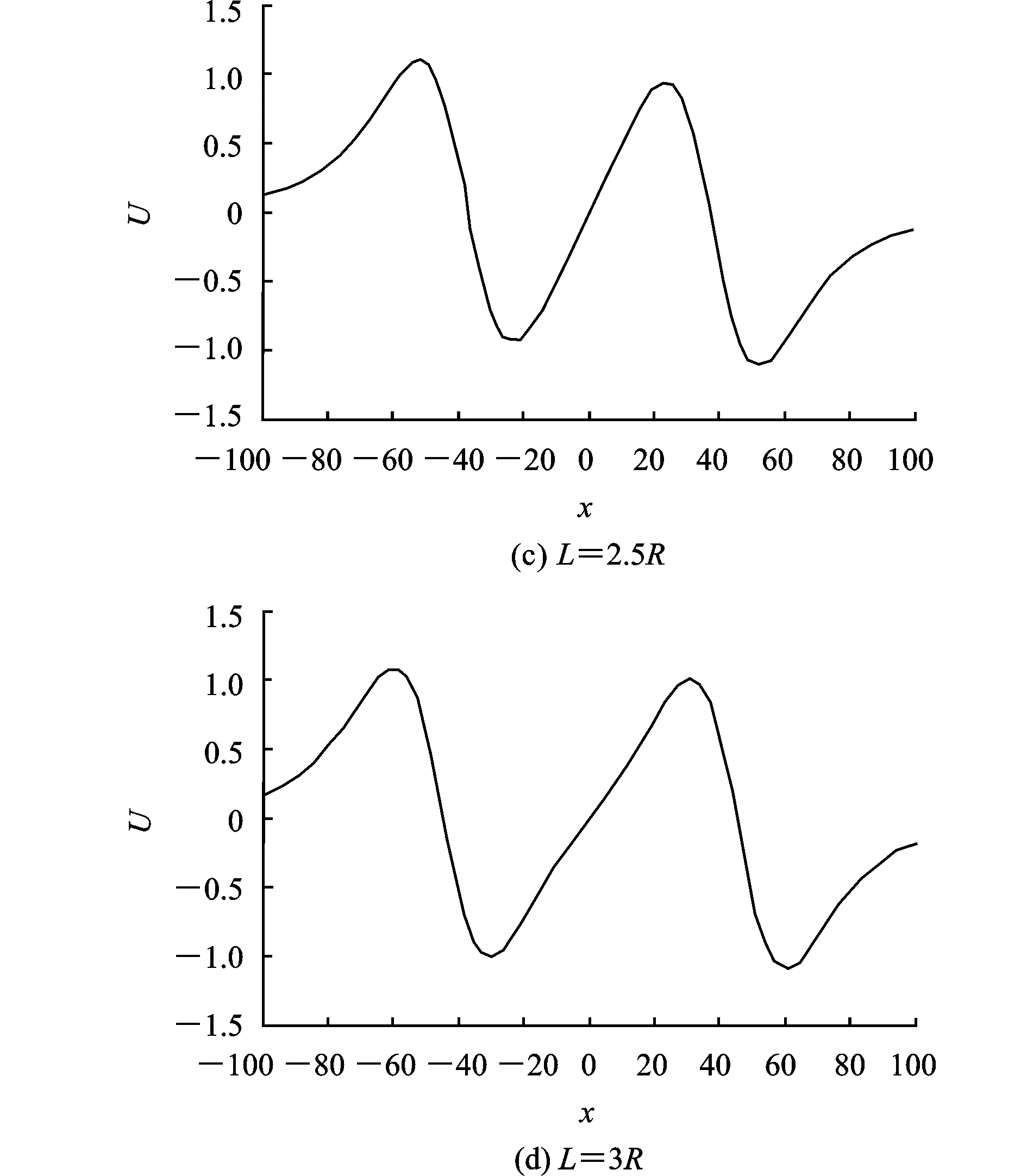
图5 感应电压随激励线圈间距离变化规律

2.3 弹载自测速试验

为了验证弹丸初速度测试精度进行了靶场回收试验，试验过程同时利用天幕靶测速作为对照。由于天幕靶与炮口位置不重合因此弹载自测速数据要加上经过外弹道西亚切定律计算出的补偿量[20]。通过微处理器的存储单元读取了10发有效数据，同时记录了天幕靶测速数据如表1所示。从试验结果看到弹丸初速度呈现出一定的跳动性。通过试验结果可知测速的平均相对误差为0.26%，该误差可满足测量的要求，这为下一步的引信作用时间的修正奠定了基础。

表1 初速度测量结果

3 六自由度刚体弹道模型

为了求得弹丸在飞行过程中的弹道诸元，通过弹道方程组构建了弹丸在非标准条件下的六自由度刚体外弹道模型，六自由度刚体外弹道模型基本可以描述弹丸实际的飞行过程[21]。弹道模型建立过程做出以下基本假设：

(1) 弹丸在整个飞行过程中的攻角为0°；

(2) 视弹丸为刚体且为理想的轴对称体；

(3) 地表为平面，g值为9.8 m/s2，同时忽略地球曲率影响；

(4) 地面系作为惯性坐标系。

六自由度刚体外弹道模型分别为

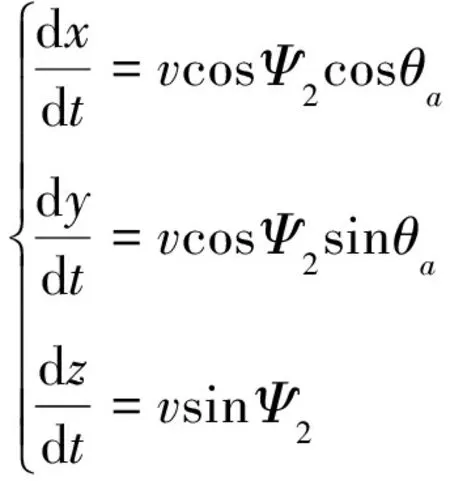
(5)

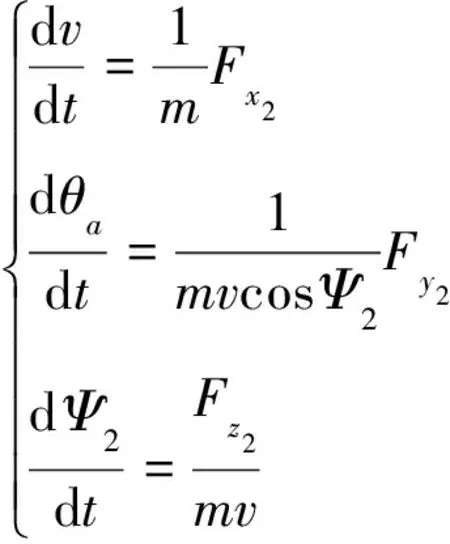
(6)

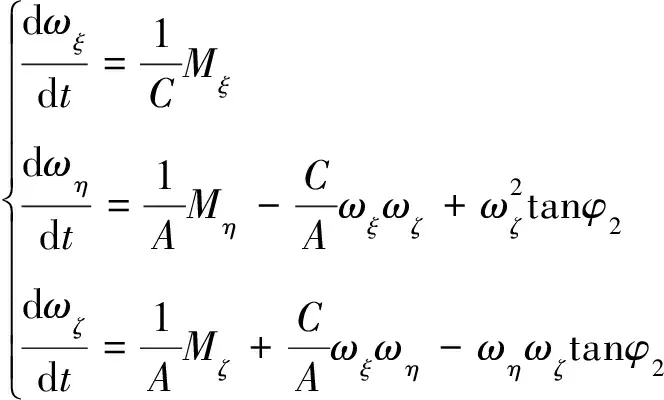
(7)

(8)

由弹丸质心运动方程的标量方程、质心位置坐标变化方程、弹丸绕质心转动的动力学方程以及弹丸绕质心运动的运动学方程组联立构建了弹丸六自由度刚体外弹道模型[22-23]。方程组中的各变量的含义以及推导过程详见文献[22，23]，文中不再赘述。

4 时间修正模型的建立

在MATLAB中调用龙格库塔法以步长为0.001 s解算弹道微分方程。弹丸的理论初速度为245 m/s，在规定的1 500 m水平射距下通过仿真可得到弹丸不同初速与引信作用时间的关系。大量测试表明，弹丸初速跳动值在±5 m/s范围内，如果不考虑弹丸初速的跳动直接把理论初速为245 m/s下的理论作用时间作为引信的作用时间必然会导致误差。现对弹丸在初速跳动范围(245±5) m/s内产生的误差进行理论分析，结果如表2所示。

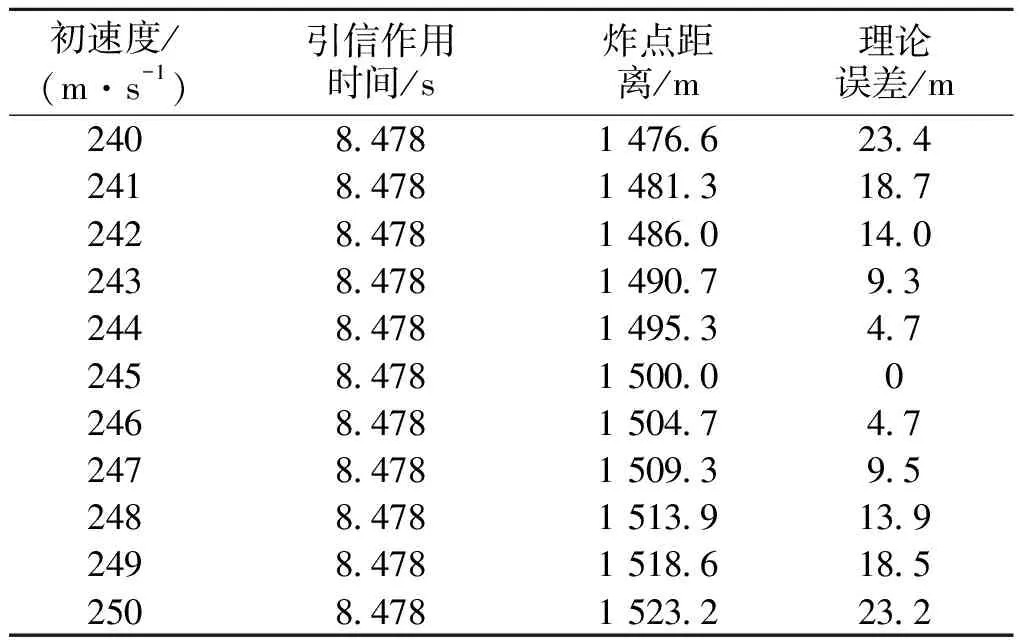
表2 理论作用时间下不同初速弹丸的定距误差

从表2可以看到实际初速度与标准初速度的跳动值越大理论误差越大。在初速跳动范围内最大的误差可达23.4 m。在水平射距1 500 m时用MATLAB仿真得到弹丸速度在240～250 m/s下引信的作用时间，以时间为因变量、速度为自变量进行线性拟合可得到时间关于初速的拟合公式

t=-0.034 69v+16.99

(9)

引信作用时间和初速的线性拟合曲线如图6所示。

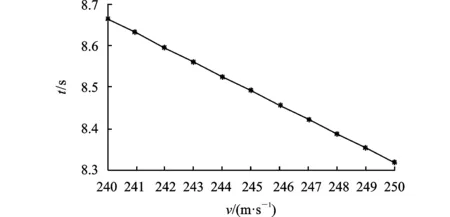
图6 炸距一定时弹丸初速与引信作用时间关系

从图6可看到离散点基本都落到直线上，下面用拟合优度R2检验线性拟合效果

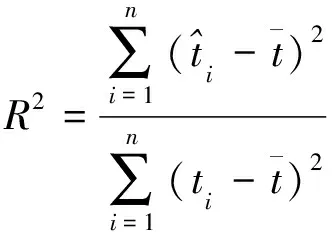
(10)

5 程序的执行流程

试验前首先把程序烧写到微处理器中，其中包括测速的程序、修正关系式、计时程序以及引爆弹丸的控制程序。试验前引信上电并完成系统的初始化，系统进入工作状态并随时准备执行弹载自测速程序。在系统完成弹丸初速的测量后可根据程序中的修正关系式实时地计算出引信的作用时间。考虑到弹载自测速存在失败的可能性，为了最大程度地减少误差，如果测速失败则把理论时间作为引信的作用的时间。当引信的作用时间确定后计时模块便开始计时，计时完成后由控制模块发出相应的信号引爆弹丸。 炸点控制系统的整体流程如图7所示。

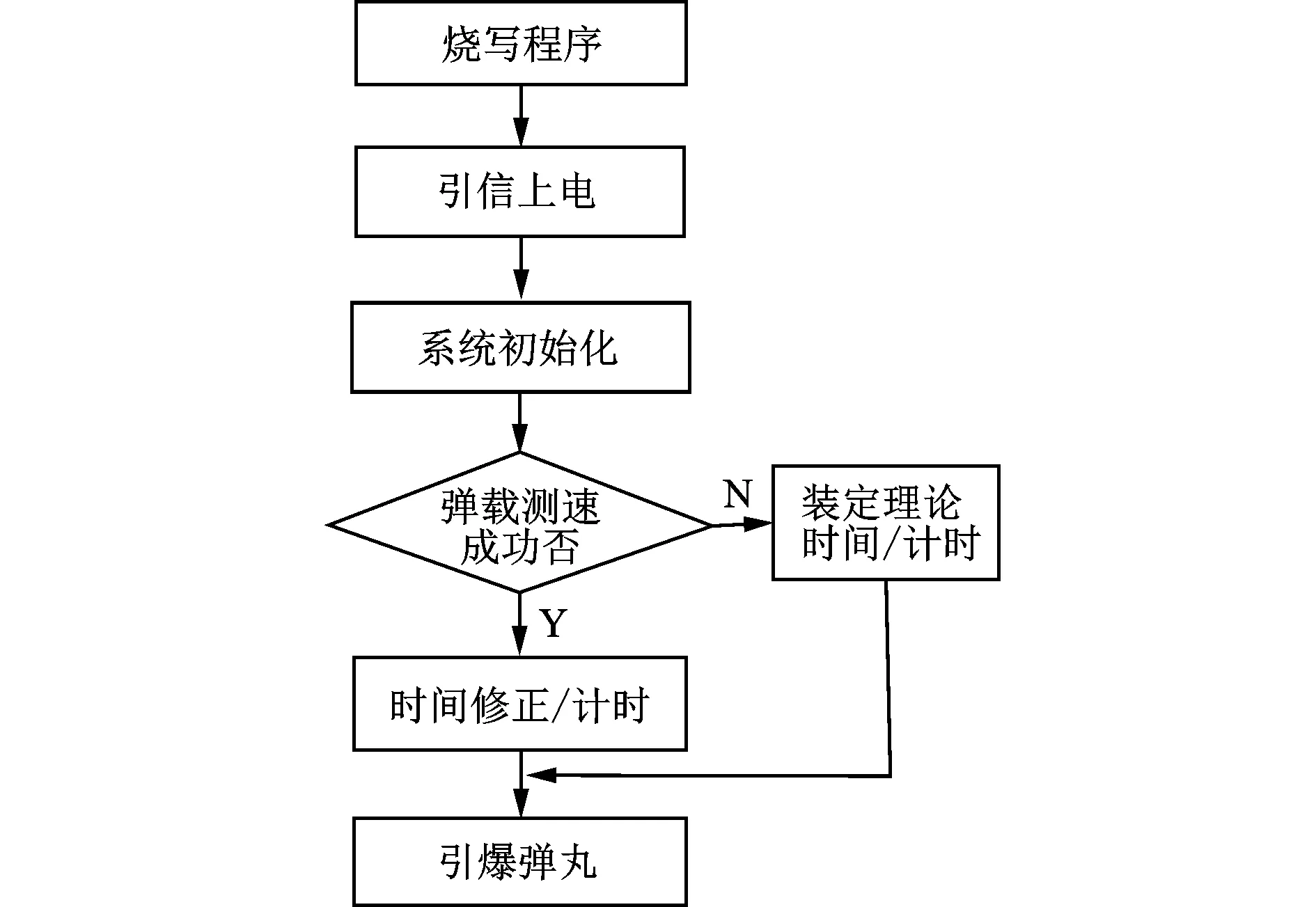
图7 弹载自测速修正的炸点控制系统程序执行流程

6 靶场空炸试验

为了检验弹载自测速修正方法炸点控制精度制作了原理样机进行靶场动态试验。设定弹丸射角为183 mil(约11°)，水平定距1 500 m进行空炸试验。试验当天的自然环境：温度为8 ℃，无风雨，大气压强为标准大气压。试验场地设立了标杆和高速摄影进行试验数据采集，试验过程记录每发弹丸的炸距并大致记录炸高。部分炸点图片如图8所示。10发有效数据的试验结果如表3所示。通过弹载自测速修正后的平均定距误差为9.6 m，弹丸的定距精度比不考虑初速跳动时提高了一倍多。

图8 空炸试验部分炸点图

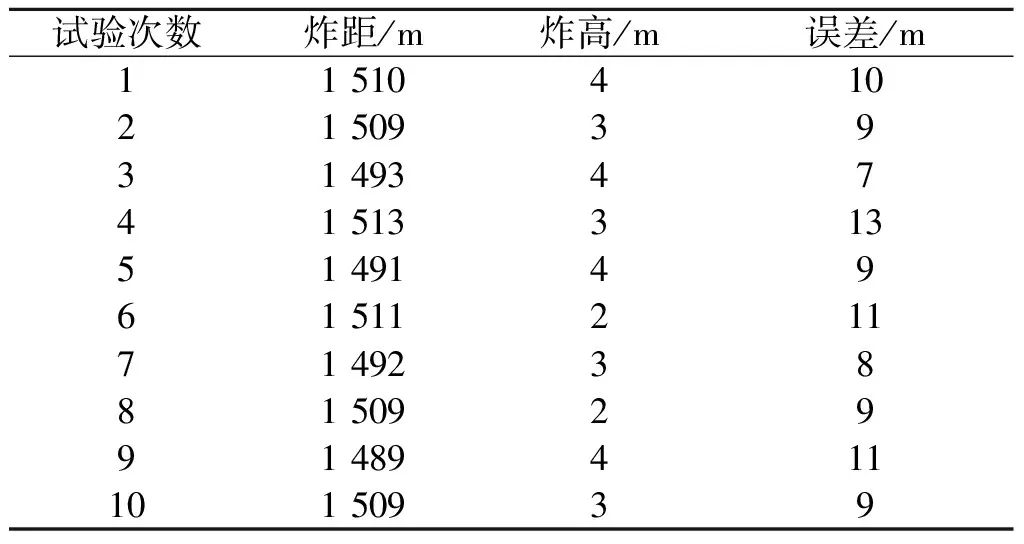
表3 靶场空炸试验结果

7 结论

本文介绍了一种弹载自测速修正的炸点控制技术。针对弹丸的初速存在跳动的问题提出了利用弹载自测速方法来修正引信作用时间以提高炸点精度的方法，此外文中重点分析了弹载自测速的实现方法和关键技术。最后通过靶场试验表明基于弹载自测速修正的炸点控制技术能有效提高弹丸的定距空炸的精度。通过分析试验误差，今后可从以下几个方面研究以进一步提高弹丸的定距空炸精度：

(1) 虽然弹道模型的建立过程考虑了实际的射击环境，但是实际试验过程中影响因素较多且难以控制。因此仍需通过大量试验来弥补仿真结果存在的误差。

(2) 实战过程持续时间较长，因而外部气象条件可能变化较大且弹丸发射角度灵活多变，需要开发稳定可靠的装定技术以应对复杂多变的发射参数。

(3) 定距精度除了弹丸初速跳动这个主要影响因素外，弹形系数、外部发射环境、弹丸的制造工艺以及成品质量也是需要考虑的内容。