莱斯衰落信道下MQAM信号调制方式自动识别方法

胡佩聪， 杨文东， 李 佩

(陆军工程大学 通信工程学院，江苏 南京 210007)

调制方式的自动识别(automatic modulation classification, AMC)是介于信号检测和信号解调之间的一项技术，其主要任务是实现信号的智能接收与处理。在合作通信领域，该技术主要用于智能无线电系统，包括认知无线电与软件无线电；在非合作通信领域，其主要用于电子对抗，通信侦察等[1]。

传统调制方式识别技术可以分为两类：基于似然比(likelihood based, LB)的调制方式识别技术[2]和基于特征(feature based, FB)的调制方式识别技术[3]。基于似然比的调制方式识别算法具有较高的准确率，但它需要信号模型中随机变量的概率分布等先验信息，而这在实际应用中通常是无法获取的。另外，该算法计算复杂度高，有的场景下仅存在理论上的计算可能。基于信号特征的调制方式识别算法计算复杂度较低，通过合理设计特征参数与分类器能获得较好的分类结果，但特征参数的设计与分类器的选择对性能影响较大。近年来，随着计算机硬件以及大数据的发展，基于深度学习的调制方式识别方法[4]被大量研究，不同架构的神经网络在调制识别领域的应用也趋于多样化，既可用作单独的特征提取器或者分类器，也可将其用作二者的结合。文献[5]采用简单结构的卷积神经网络(convolutional neural network, CNN)对通信信号进行调制识别，并与传统基于特征参数结合决策树、支持向量机(support vector machine，SVM)等分类器的方法进行了比较，展示了CNN在信号调制识别方面的有效性。文献[6]在此基础上对CNN架构改进，通过增加卷积层数提高了识别准确率，并研究了ResNet、DenseNet和CLDNN等模型的调制方式识别性能。文献[7]分别采用CNN与循环神经网络(recurrent neural network，RNN)对AWGN信道和瑞利衰落信道影响下的6种信号调制方式进行分类，并将该算法与传统基于高阶累积量结合SVM分类器算法比较，验证了该算法在分类精度上具有优越性。文献[8]介绍了CNN的变体VGGNet在调制方式识别领域的应用，表明其在低信噪比下相较于采用SVM方法具有较高的识别准确率。文献[9]结合信号的瞬时特征与高阶累积量特征，使用深度神经网络(deep neural network, DNN)分类器，在AWGN信道条件下对13类调制信号进行了有效分类。

以MQAM为代表的复杂高阶调制信号以其高效的频带利用率被广泛应用于各种有线通信以及无线通信场合，对该类信号的调制识别技术一直以来是研究热点。文献[10]通过修正的联合功率估计调制识别算法构造混合高阶矩特征参数，使用Fisher准则对瑞利衰落信道下的32QAM、64QAM以及128QAM三类信号进行分类，在信噪比大于5 dB时获得了超过98%的识别准确率，但该方法对判决阈值的设置要求较高。文献[11]提出基于信号星座图与深度学习相结合的方法进行数字信号调制识别，但该方法对高阶QAM信号分类效果欠佳。文献[12]提出了一种联合四阶累积量、零中心归一化幅度紧致性和减法聚类计算聚类中心密度值的方法对MQAM调制方式进行识别，该方法不需要预先知道信号的波特率与载波频率，但由于采用逐级分类的方法，对各级的识别准确率要求较高，易产生错误传递。文献[13]结合六阶累积量和两步特征提取结构，提出一种通过降低待识别信号调制阶数的方法对QPSK、16QAM以及64QAM信号进行识别。以上文献分析的QAM信号或者种类数量受限，或者信道环境较为理想。因此，本文将研究对象确定为受莱斯衰落影响的4QAM、16QAM、32QAM、64QAM、128QAM、256QAM六类信号。首先通过星座图分析莱斯衰落对该类信号的影响，然后分别用CNN模型以及信号特征参数结合DNN分类器模型对受不同程度莱斯衰落的信号进行分类并对比分析性能。在特征参数选取上，本文提出直接采用多个混合高阶矩作为特征参数对MQAM信号进行分类，该方法与传统采用高阶累积量作为特征参数的方法相比识别性能有明显提升。

1 信号模型

接收端信号模型表示为

r(t)=aej(2πtf0+θc)s(t)+ω(t)

(1)

式中：a表示信道衰落，f0表示频率偏移，θc表示相位偏移，ω(t)表示零均值的加性复高斯白噪声。s(t)为输入信道的带通MQAM信号，可表示为

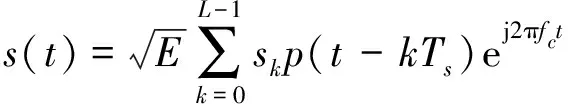
(2)

式中：E为信号能量，L为码元序列长度，sk为MQAM码元序列，p(t)为发送码元波形，Ts为码元宽度，fc为载波频率。在接收端对信号进行下变频，匹配滤波等预处理，得到受衰落影响的基带符号序列。

莱斯分布又称广义瑞利分布，其概率密度函数为

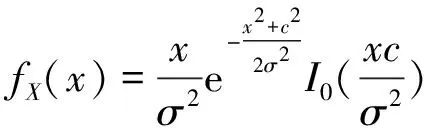
(3)

式中：c2表示镜像分量(直射分量)的功率，σ2表示散射分量的功率，I0(·)表示第一类零阶贝塞尔函数。莱斯K因子定义为镜像分量和散射分量功率之比，表达式为

(4)

此时，概率密度函数可由莱斯K因子表示为

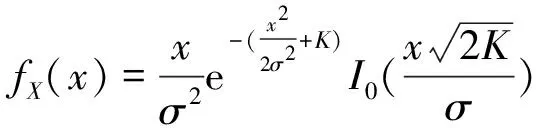
(5)

莱斯K因子决定了衰落程度，当莱斯K因子趋于零时(K<-40 dB)，即不存在镜像分量的情况下，莱斯分布退化为瑞利分布，当莱斯K因子足够大时(K>15 dB)，莱斯分布趋于高斯分布。图1以1 000个样点的16QAM星座图为例，展示了相位偏移为0，信噪比分别为15和20 dB时不同莱斯K因子对信号的影响。从图1可以看出，莱斯衰落对信号的影响体现在两个方面，一是对信号的尺度进行了放缩，二是使信号的相位产生了偏移。进一步通过对比可以看出，随着信噪比的升高，星座图各点区分越发明显，在相同信噪比条件下，莱斯K因子越大，越接近理想信道下的星座图。

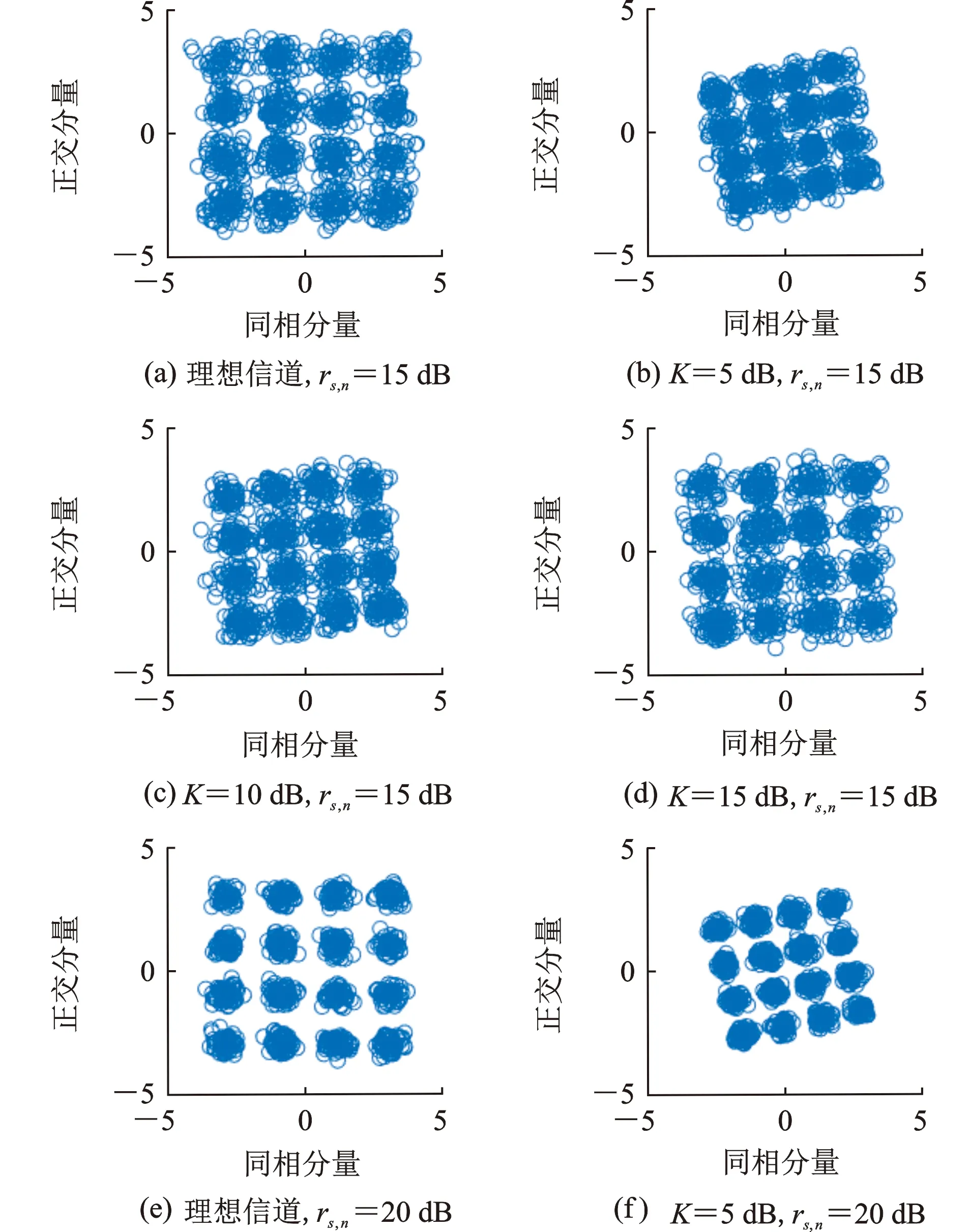
图1 16QAM信号受不同程度莱斯衰落影响的星座图

2 MQAM调制方式识别方法

2.1 基于CNN模型的识别方法

2.1.1 数据集

本文用MATLAB对莱斯衰落影响下的4QAM、16QAM、32QAM、64QAM、128QAM以及256QAM六类信号进行仿真并产生相应的训练以及测试数据集。训练数据集中每类调制方式产生50 000个带标签的信号序列，每个信号序列长度L=200，接收的第i个符号序列满足ri(n)=aiejθisi(n)+ωi(n)，其中n=1,2,…,L，ωi(n)～CN(0,1)，θi服从[0,π/4]之间的均匀分布，ai服从莱斯分布，同一符号序列ai相同，不同符号序列之间ai不同，每个符号序列的平均信噪比服从[0 dB,30 dB]之间均匀分布。测试的数据集采用与训练数据集相同的信噪比范围，测试数据的信噪比间隔为2 dB，每类调制信号序列对应于相应信噪比采用蒙特卡洛方法产生1 000个符号序列。

2.1.2 CNN结构

CNN是一种前馈神经网络，它的神经元之间的连接模式受动物视觉皮层的启发，一般由输入层、卷积层、池化层、全连接层以及输出层组成。在过去几年，CNN在视频自动分类、语音识别、图像分类等领域展现了强大的性能，其在特征提取上的优异表现十分契合信号调制方式识别的需求，引起了相关领域研究者的关注。本文参考文献[6]改进的CNN模型，卷积神经网络结构如图2所示。

图2 CNN结构

(1) 输入层

输入层用于接收数据，通常要求数据具备3个维度，分别是长度、宽度和通道。因此，在将复基带符号序列作为输入时需要对其进行预处理：一是将信号拆分为实部和虚部，二是将信号扩展成三维。

(2) 卷积层

卷积层使用卷积核与输入层的局部区域相连接，通过每个核共享参数在输入数据中检测块内特征，实现从特定模型中提取特征的功能。其具体参数设置如下：第一个卷积层的卷积核数为64，卷积核大小为1×3，卷积步长为1；第二个卷积层的卷积核数为64，卷积核大小为2×3，卷积步长为1；第三个卷积层的卷积核数为16，卷积核大小为1×3，卷积步长为1；第四个卷积层的卷积核数为16，卷积核大小为1×3，卷积步长为1。每个卷积层均采用偏差项，偏差项采用零均值初始化方法，权重初始化采用Glorot均匀分布初始化方法，不采用正则项与权重约束，激励函数为ReLU，补边方法定义为Valid。

(3) 全连接层

该层的每个神经元与相邻层的所有神经元进行连接，但层内不共享任何连接。第一层网络节点数为128，激励函数为ReLU，第二层网络节点数为输出类别数，激励函数为Softmax。

在卷积层与全连接层连接时，需要通过Flatten层将数据的二维特征一维化，以完成向全连接层的传递。

2.1.3 训练参数设置

训练参数的选择对神经网络的性能有着至关重要的影响，为防止发生过拟合，在模型训练过程中，本文在Flatten层前采用Dropout层按照一定概率随机排除一部分输入神经元，将其暂时从网络中丢弃，参数设置为0.5，与文献[5]中的CNN2模型一致。将训练数据集的15%作为验证集，用于测试网络的训练效果，神经网络采用的损失函数为多类别交叉熵，优化方法为自适应矩估计(Adam)，学习率为0.001，学习率更新参数β1=0.9,β2=0.999，模糊因子ε=10-8，每批次训练的数据量为100个信号序列(batch_size=100)，所有数据训练一次为一次迭代(Epoch)，训练的停止条件为Epoch达到100次或者训练损失值连续10个Epoch没有改善，与文献[4]中的CNN模型一致。

图3以莱斯K因子为0 dB时产生的数据集为例，展示了CNN模型的训练损失与测试损失曲线对比。从图中可以看出，在进行第14次迭代时，测试的损失值达到最小，一般此时测试准确率最高，根据设置的训练终止条件，在第24次迭代时训练终止，最终CNN的网络权重采用第14次迭代时的网络权重。

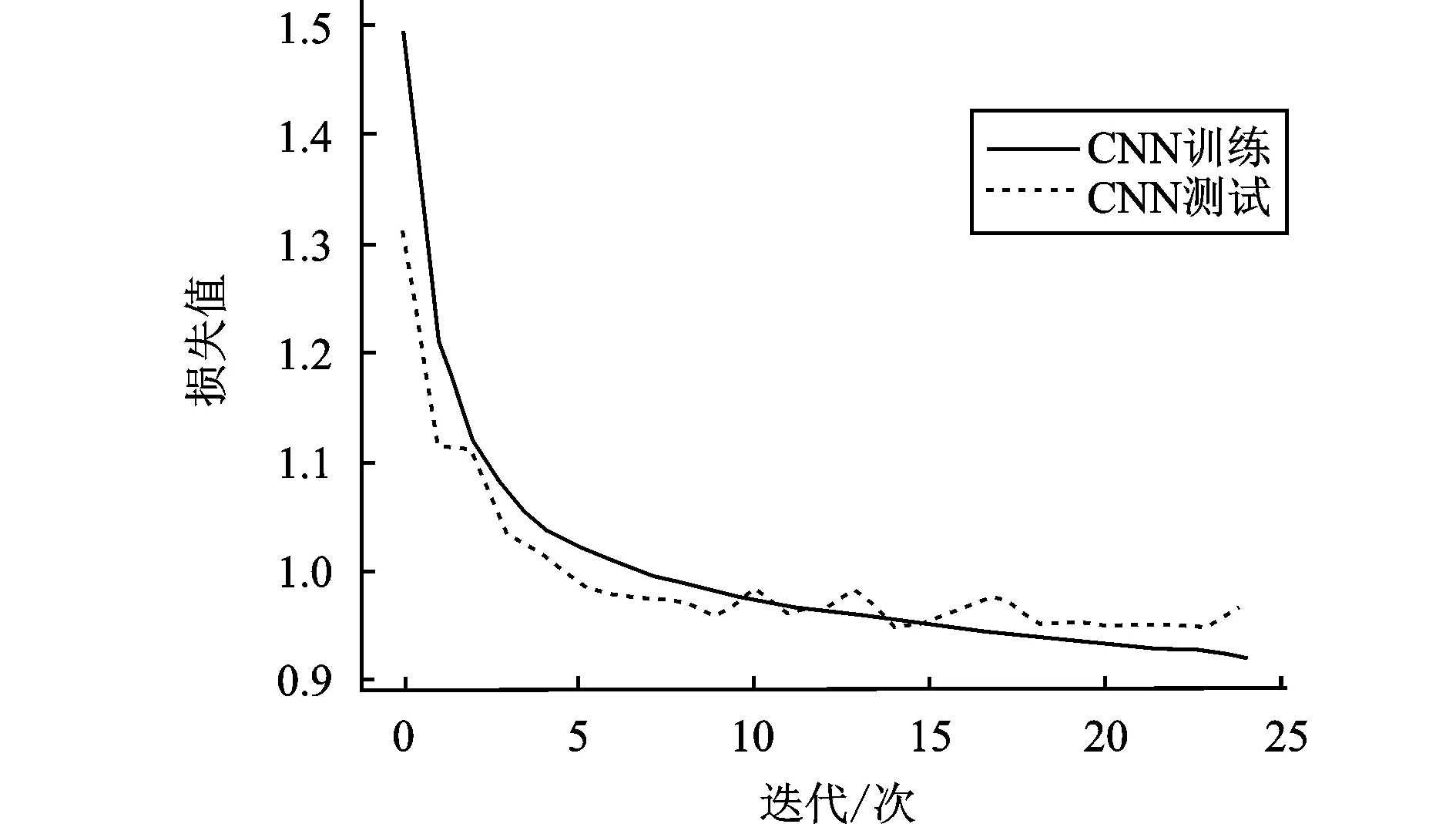
图3 CNN训练损失与测试损失

2.2 基于特征参数结合DNN模型的识别方法

2.2.1 特征参数

复平稳随机过程{x(n)}的p阶混合矩定义为

Mpq=E[x(n)p-qx*(n)q]

(6)

式中:x*(n)为x(n)的复共轭，p为阶数，q为共轭的位置。其各高阶累积量表达式为

对于与信号相互独立的加性高斯白噪声，当阶数大于2时，其高阶累积量的理论值为0，因此高阶累积量有较强抑制噪声的能力，其作为特征参数用于调制方式识别已被广泛研究。对于MQAM信号，有些高阶累积量的理论值恒为零(如C41与C60等)，选择这些量作为特征参数将毫无意义。经过计算，采用特征参数集U1={|C40|,|C42|,|C61|,|C63|,|C80|}作为分类器的输入。在对信号去除噪声能量干扰并进行能量归一化后，选取的各高阶累积量特征参数理论值如表1所示。

表1 高阶累积量特征参数理论值

高阶累积量由不同阶的混合高阶矩多项式组合而成，其本质上是在信号混合高阶矩的基础上进一步进行特征提取的过程。对于使用DNN分类器进行调制识别的方法，可将混合高阶矩直接交给神经网络进行特征提取与分类。为方便与高阶累积量特征参数进行比较，分别采用包含5个混合高阶矩的特征参数集U2={|M40|,|M42|,|M61|,|M63|,|M80|}与包含7个混合高阶矩的特征参数集U3={|M40|,|M42|,|M61|,|M63|,|M80|,|M82|,|M84|}作为分类器输入。在对信号去除噪声能量干扰并进行能量归一化后，选取的各混合高阶矩特征参数理论值如表2所示。

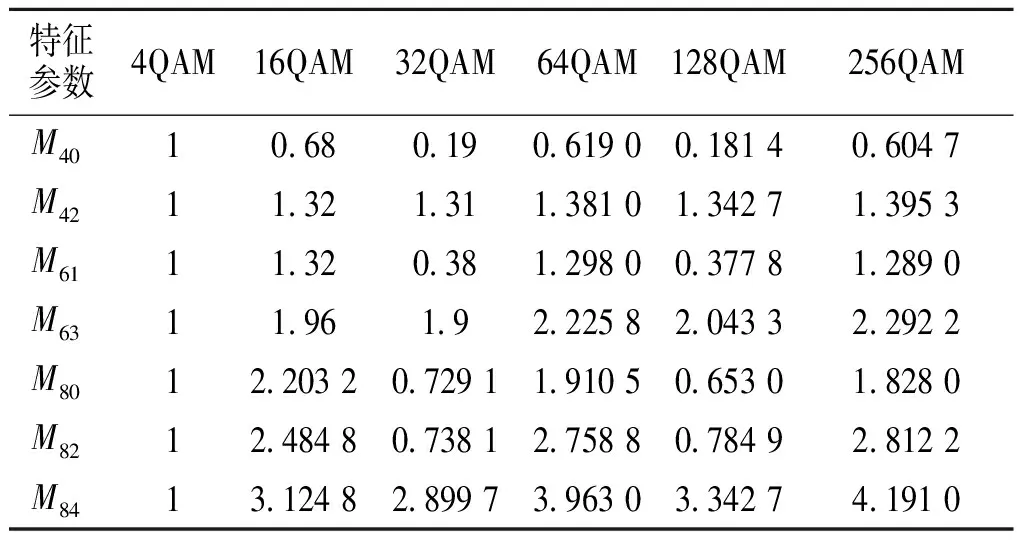
表2 混合高阶矩特征参数理论值

2.2.2 DNN分类器

DNN作为信号调制方式识别分类器能有效克服传统分类器存在的分类规则设计困难等问题，可获得较好的调制识别性能。DNN一般由输入层、隐藏层和输出层组成，每一层有一个或多个神经元。该网络的主要特点是每个神经元都接收来自前一层的各神经元作为输入，并将其输出馈送到下一层中的每个神经元。本文采用的DNN结构如图4所示。输入层维度为特征参数的数量(F1,F2,…,Fm)，隐藏层层数为4，维度分别为32，64，64，32；输出层维度为待分类调制方式类别数。隐藏层激活函数为ReLU，输出层激活函数为Softmax；损失函数为多类别交叉熵；优化方法为Adam，学习率为0.001；采用偏差项，偏差项采用零均值初始化方法；网络权重初始化采用Glorot均匀分布初始化方法；不采用正则项与权重约束。为便于比较，特征参数结合DNN分类器模型的信号参数与CNN模型的信号参数一致，其训练数据集为接收信号经处理后获得的特征参数集，训练过程设置与CNN模型一致，每批次训练的数据量为100组特征参数，所有参数训练一次为一次Epoch，训练的停止条件为Epoch达到100次或者训练损失值连续10个Epoch没有改善。

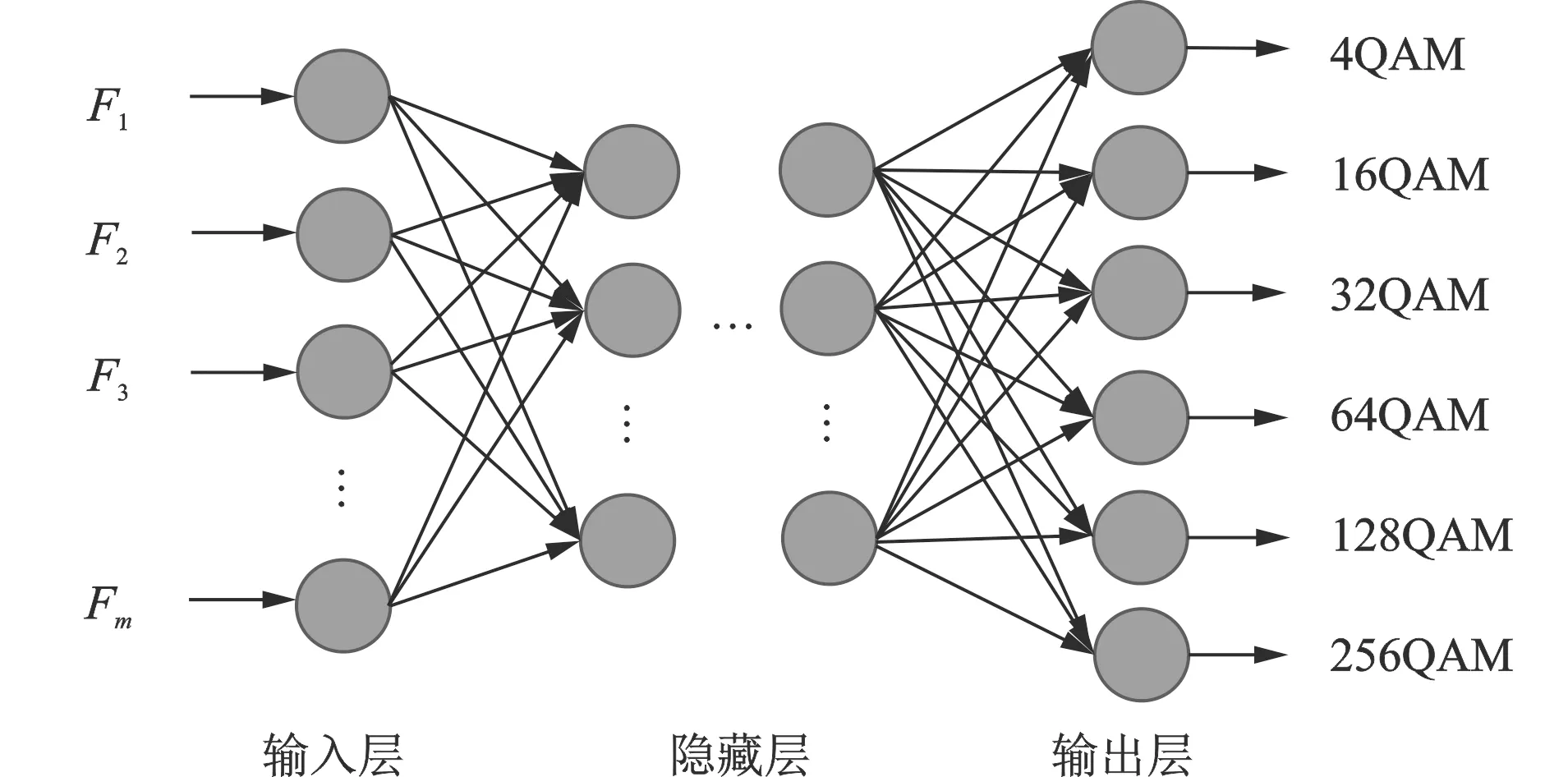
图4 DNN分类器结构

3 仿真结果与性能分析

为深入研究莱斯衰落对各模型分类性能的影响，本文仿真产生了莱斯K因子为0、5和10 dB时的MQAM数据集，分别采用CNN模型以及特征参数结合DNN模型的调制方式识别方法进行分类，并比较它们的性能。图5展示了以上各模型的识别性能，从图中可以看出，随着信噪比rs,n的提升，信号调制识别的准确率逐渐上升，且莱斯K因子越大，分类性能越好。基于特征参数结合DNN的模型存在性能上限，当信噪比高到一定程度后，分类性能不再提高，但该模型能较好地对抗莱斯衰落，不同莱斯衰落程度的准确率曲线较为接近。

图5 各模型识别准确率

以莱斯K因子为10 dB时产生的MQAM数据集为例，图6展示了在该数据集下各模型的识别准确率对比。

图6 各模型识别准确率对比(K=10 dB)

从图中可以看出，CNN模型在高信噪比条件下(rs,n>24 dB)获得了最好的识别性能，但如此高的信噪比现实中很难达到。相比CNN而言，在低信噪比下，特征参数结合DNN模型展现了其在识别率上的优势。通过不同特征参数集下分类准确率的对比可以看出，采用高阶混合矩作为特征参数的性能上限明显高于采用高阶累积量作为特征参数，且采用的参数越多，性能越好。

为研究各类信号的具体识别情况，本文对CNN模型以及特征参数集U3结合DNN模型的分类混淆矩阵进行了仿真。图7展示了信噪比为24 dB时两种方法的混淆矩阵，从图中可以看出，基于CNN的方法分类的困难集中于64QAM、128QAM以及256QAM三者之间的区分，这3类信号的识别准确率相对偏低且存在相互间的误识别，原因在于高阶QAM数据本身非常接近，再加上衰落与噪声的影响，导致CNN对高阶QAM误判率比较高。基于高阶混合矩与DNN方法分类的困难在于32QAM与128QAM之间、64QAM与256QAM之间的区分，原因在于其特征参数理论值非常接近，再加上衰落与噪声的影响，增加了误判的可能性。

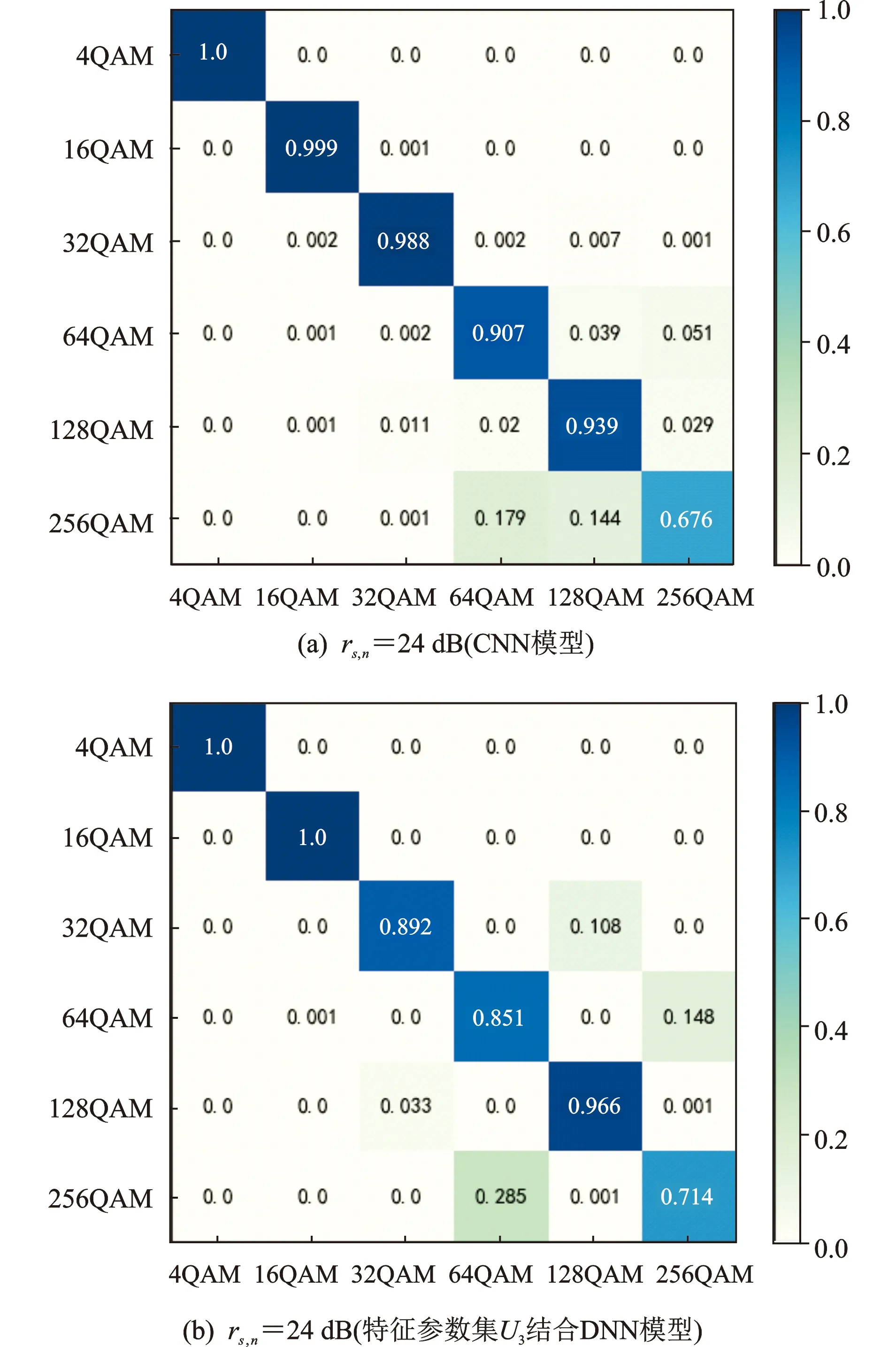
图7 混淆矩阵

4 结论

本文对莱斯衰落影响下的MQAM信号特点进行了研究，分别用CNN模型与特征参数结合DNN模型对6类QAM信号进行了分类并作了性能比较。实验重点研究了基于混合高阶矩与DNN结合的方法，仿真结果表明，该分类方法在一定程度上能对抗莱斯衰落对信号的影响，在低信噪比下识别准确率优于CNN模型，且无需带标签的数据集，具有较高的实用价值，同时与采用高阶累积量作为特征参数的方法相比,该方法识别效果优势明显。