声场波数积分截断波数自适应选取方法

李承帮，江鹏飞，孙军平，衣雪娟，林建恒

(1.中国科学院声学研究所北海研究站，山东青岛 266114；2.中国科学院大学，北京 100049)

0 引 言

波数积分法是一种常用的水下声场计算方法，此方法对波数域格林函数进行直接的数值积分，因而被认为是一种精确的声场计算方法。波数积分法由Pekeris引入到水下声场的计算中[1]，此后很多学者对其具体实现方法进行了研究。DiNapoli 等[2]基于波数积分理论提出了声场计算效率非常高的快速场程序(Fast Field Program)，Schmidt[3-4]提出了直接全局矩阵法实现声场的波数积分计算，骆文于等[5-6]提出了一种可稳定计算Pekeris 波导中声场的波数积分方法。

波数积分法的一个重要步骤是对波数域格林函数进行逆汉克尔变换，此处会面临半无限区间的积分问题。一般来说，当水平波数大于某一个临界值时，波数域格林函数的幅值会随着水平波数的增大而衰减，并趋向于0。因此通常的做法是，当波数域格林函数幅值衰减到一定程度时，对波数积分区间进行截断，忽略大于此波数积分区间的声场。若截断波数取值太大，会增加不必要的运算量；若截断波数取值太小，则会给声场的计算带来误差。积分截断相当于给波数域格林函数加矩形窗，在截断处引入了不连续点，导致出现截断效应[7]。然而频率、介质类型、波导参数、声源与接收点的相对深度等参数会对波数域格林函数的衰减特性产生很大的影响，在计算出波数域格林函数之前很难对截断波数进行合适的选取。

在不同介质类型的海洋波导中，波数域格林函数会有不同的衰减特性。对于不含冰盖层且海底为液态的海洋波导，波数域格林函数的衰减特性比较简单，当水平波数大于临界值时，波数域格林函数不存在极点；而对于存在弹性海底或冰盖层的海洋波导，在波数域格林函数衰减较慢，在水平波数大于临界值的较大范围内，很远的位置仍包含声场的重要成分[7]。本文主要关注的是各层均为流体的海洋波导中，宽带声场波数积分计算的截断波数选取问题。

当海洋波导中各层介质都是流体时，目前最常用的截断波数选取方法是把波导内最小声速对应的波数k0=ω/cmin作为一个参考波数，截断波数取值为kt=ξ·k0，其中ξ取一个固定的值。文献[8]认为ξ可取1.1；文献[9]认为大多数情况下ξ取1.1～1.2 时即可包含波数域格林函数中绝大部分能量。在宽带声场计算过程中，若ξ取固定值，则不能兼顾低频段的积分精确度和高频段的计算量。文献[10]提出一种消除截断效应的方法，在波数域格林函数截断点后，添加埃尔米特(Hermite)多项式函数，消除截断处的不连续性并使其迅速衰减。该方法虽然能避免出现截断效应，但是会给声场计算带来一定的误差。文献[11]提出了基于预估-校正思想的最大截止波数自动选取算法。但此方法需要在波数域格林函数计算过程中判断是否进行积分截断，这不利于实现波数域格林函数的并行计算。

针对上述问题，本文提出一种应用于宽带点声源声场计算的积分截断波数自适应选取方法。首先构造一个数学模型拟合水平波数大于参考波数时的波数域格林函数，然后利用卡尔曼滤波器对模型的参数进行跟踪和预测，再根据已计算频率的模型参数估计出下一频率的模型参数，最后将估计的模型参数代入数学模型求解出下一个频率的截断波数，从而实现给定精确度下的积分截断。

1 截断波数自适应选取方法

在利用波数积分法计算频率为f的点声源产生的声场时，需要对波数域格林函数G(kr;f)进行逆汉克尔变换：

式中：J0(krr)为零阶贝塞尔函数，r为水平距离，kr为水平波数。当kr大于某个临界值时，G(kr;f)随kr的增大而衰减，在G(kr;f)明显衰减后进行积分截断不会带来很大误差。本文将积分截断波数记为kt，kt的取值取决于波数域格林函数的衰减特性，即G(kr;f)开始衰减的位置以及衰减的速率。

考虑频率为fn=f0+n·Δf的宽带点声源声场的计算问题，其中n=1，…，N，Δf是频率间隔。由1.1节的算例可看出，随频率fn的变化，G(kr;fn)呈现出一定的变化规律。因而可根据已计算的G(kr;f0)，G(kr;f1)，…，G(kr;fn)的衰减特性，估计G(kr;fn+1)的衰减特性。但由于G(kr;f)是数值计算的结果，为了便于跟踪和预测它的衰减特性，需要构造一个合适的数学模型对其进行拟合，并利用自适应滤波器对此数学模型的拟合参数进行跟踪和预测。根据模型参数的预测结果，可计算出下一个频率满足精度要求的截断波数。

1.1 波数域格林函数的衰减特性

本节分析波数域格林函数的衰减特性，以选取合适的数学模型对其进行拟合。在Pekeris波导中，水层的波数域格林函数G1(kr;f)可表示为声源项与上行波、下行波的叠加：

式中：A+1(kr)、A-1(kr)分别表示上行波、下行波的波谱数；kz，1=k1是水层的波数；z是接收深度，zs是声源深度；Sω是声源强度。文献[12]中指出当水平波数kr比较大时，在包含声源的介质层中，式(2)中的声源项具有最慢的衰减速率，因而G1(kr;f)的衰减速率主要由声源项决定。

以下讨论G1(kr;f)中声源项的衰减特性。用ϕs表示式(2)中声源项的对数幅值，表达式为

令ξ=kr/k1，则kr=ξ·k1。当kr＞k1时，ξ＞1，且把上述kz，1和kr代入式(3)中并化简可得：

当ξ＞1时，将其代入式(4)，可得：

当ξ→1 时，ϕs(ξ;f) →∞；当ξ≫1 时，ξ≈将其代入式(4)中，可得：

在Pekeris 波导中，由式(5)和式(6)可知当ξ＞1时，声源项的对数幅值ϕs(ξ;f)随ξ的变化关系近似满足一次线性项与对数项的叠加。

在海底为液态且没有冰盖层的海洋波导中，波数域格林函数G(kr;f)也会呈现与Pekeris波导类似的衰减特性。令参考波数k0(f)为水平分层介质中最小声速对应的波数：

其中：cm表示第m层介质中的声速。当kr＞k0(f)时，任意一层介质的垂直波数都为纯虚数。与Pekeris 波导中的情况类似，当kr＞k0(f)时，G(kr;f)会随kr的增大而减小，并趋向于0。对G(kr;f)的幅值取对数，并且把水平波数kr与参考波数k0(f)的比ξ作为自变量，令：

其中，水平波数比ξ的表达式为

ϕ(ξ;f)能较好地反映G(kr;f)的衰减特性。以图1中的波导环境为例，首先计算出不同频率的波数域格林函数G(kr;f)，然后计算出对应的ϕ(ξ;f)，计算结果如图2 所示。可以看出当ξ≥1，即kr≥k0(f)时，G(kr;f)开始衰减。频率越高，G(kr;f)衰减得越快。

图1 海洋波导环境特例Fig.1 A special case of marine waveguide environment

图2 不同频率波数域格林函数对数幅值Fig.2 Logarithmic magnitude of Green's function in wavenumber domain at different frequencies

设期望的积分截断精确度参数为a，表示期望在ϕ(ξ;f) =-a处进行积分截断。当a分别取3，4，5，6 时，计算在期望截断处ξt的取值随频率变化，结果如图3所示。结合图2的分析结果，可以看出在较低频段，截断波数比ξt需要取远大于1的值才能获得足够的积分精确度。其原因是在低频段ϕ(ξ;f)衰减得比较慢，而在较高的频段ϕ(ξ;f)衰减得比较快，截断波数比ξt取稍大于1的值就能获得足够的积分精确度。

图3 截断波数与参考波数的比随频率变化Fig.3 The ratio of truncated wavenumber to reference wavenumber versus frequency

目前常用的截断波数选取方法是令ξt等于某个固定的值。在宽带声场计算中，若ξt取一个较大的值，可保证在低频声场计算时获得足够的积分精确度，但会给高频声场计算增加不必要运算量；若ξt取定一个较小的值，可减少高频声场的计算量，但会增大低频声场计算误差。

1.2 波数域格林函数的模型拟合

由1.1节的分析，在海底为液态且没有冰盖层的海洋波导中，当kr≥k0(f)时，G(kr;f)开始衰减并趋向于0。在保证精确度的条件下，为了减少计算量，截断波数的取值应尽可能小，所以应当更关注当kr不太大时G(kr;f)的衰减特性。

对于格林函数中的声源项，根据本文1.1节中式(4)～(6)，当ξ＞1时，ϕs(ξ;f)随ξ的变化近似满足对数项与线性项叠加的关系，且当ξ→1 时，ϕs(ξ;f) →∞；对于格林函数中的齐次项，当kr的值不太大时，其影响也需要考虑，但由于齐次项包含数值计算结果A+1(kr)和A-1(kr)，难以对其变化特性进行理论推导分析。

图2中格林函数对数幅值ϕ(ξ;f)的数值计算结果显示，在1 ＜ξ＜2 的范围内，当ξ接近于1 时ϕ(ξ;f)衰减速率较快；随着ξ的增大，ϕ(ξ;f)的衰减速率逐渐减慢。ϕ(ξ;f)的这种变化特征与声源项ϕs(ξ;f)所满足的对数和线性变化特征比较相似。另外，注意到式(2)中格林函数每一项都包含kz，1，因而ϕ(ξ;f)中每一项都包含且ξ=1 是ϕ(ξ;f)的一个极点。而在数值计算中，ξ=1处格林函数的计算结果不是无穷大，且极点的位置可能会存在偏差。因此，构造数学模型时，不应完全按照格林函数表达式把ξ=1确定为极点，而应该把该极点的位置作为一个可调整的参数，否则数学模型可能与格林函数的数值计算结果失配。

基于上述对格林函数衰减特性理论和数值计算结果的分析，并参照式(5)和式(6)中ϕs(ξ;f)的近似结果，构造了以下包含对数项和一次线性项的数学模型：

或

其中：ϑ=[ϑ1ϑ2ϑ3ϑ4ϑ5]T和θ=[θ1θ2θ3θ4]T为模型参数，ξt为截断处的水平波数比，1 ≤ξ≤ξt。根据对数函数的性质，可证明式(10)和式(11)是等效的，而式(11)的参数更少，因此采用式(11)作为格林函数的拟合模型。在该模型中可以通过调整参数θ2去调整极点的位置，避免了因ξ=1附近极点位置的偏差而导致的模型失配。

利用此模型通过最小二乘法对格林函数对数幅值进行拟合：

图4 是利用式(11)中的数学模型对不同频率ϕ(ξ;f)的拟合结果，图中粗虚线对应图2中各频率的波数域格林函数对数幅值ϕ(ξ;f)，实线是拟合结果。所有频率的ϕ(ξ;f)与对应的拟合曲线几乎重合，这表明利用式(11)对ϕ(ξ;f)进行拟合取得了较好的效果。

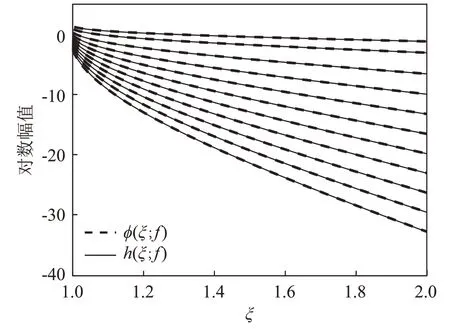
图4 波数域格林函数对数幅值拟合结果Fig.4 Fitting results of the logarithmic magnitude of Green's function in wavenumber domain

本文构造的式(11)中的数学模型符合格林函数的变化趋势，具有一定的物理意义，可调整极点的位置，避免模型在极点处失配，并且复杂程度较低。因此，本文将采用式(11)中的数学模型对格林函数对数幅值ϕ(ξ;f)进行拟合。

1.3 模型参数自适应滤波

卡尔曼滤波器是一种最优线性状态估计方法，被广泛应用于工程领域，本文利用卡尔曼滤波器对波数域格林函数的拟合参数进行跟踪和预测。1.2节构造的数学模型h(ξ;θ)中包含4 个参数θj(n)，j=1，2，3，4，n是频率序号。这4个参数之间是相互独立的，用4个卡尔曼滤波器分别对其进行跟踪和预测。

式(11)中第j个参数的状态方程为

第j个参数的观测方程为

其中：zj(n)是状态的观测值；观测矩阵H=[1 0]T；vj(n)为观测噪声，设观测噪声的协方差矩阵是Rj。

设第j个参数、第n步的卡尔曼增益矩阵为Kj(n)。卡尔曼滤波的每个迭代过程，都包含了预测与修正两个环节，在这两个环节中都会对状态矢量sj和状态误差协方差矩阵Mj进行更新。为了对两个环节的变量加以区别，用sj(n|n-1)表示根据第n-1 步状态矢量所预测的第n步状态矢量，Mj(n|n-1)表示根据第n-1步状态误差协方差矩阵所预测的第n步状态预测误差协方差矩阵；用sj(n|n)表示第n步修正后的状态矢量，Mj(n|n)表示第n步修正后的状态误差协方差矩阵。

对每个模型参数θj(n)分别进行卡尔曼滤波，其具体计算为[13]

(1) 初始条件

(2) 预测

(3) 状态预测误差协方差矩阵

(4) 卡尔曼增益

(5) 修正

(6) 状态误差协方差矩阵

其中：I为单位矩阵。

1.4 截断波数的计算

设期望的积分截断精确度参数为a，表示期望在波数域格林函数的幅值衰减到10-a时进行积分截断，即：

其中：kt为截断波数。

把自适应滤波器输出的第n+1个频率的参数估计结果代入数学模型式(11)中，可估计出第n+1个频率的波数域格林函数：

把式(21)代入式(22)中可得第n+1 个频率的截断波数ξt(fn+1)即为式(23)的解。

由式(11)可知方程(23)是超越方程，需要通过数值方法求解。

1.5 截断波数自适应选取流程

图5是本文提出的截断波数自适应选取方法的流程图。本文提出的截断波数自适应选取方法包含以下步骤：

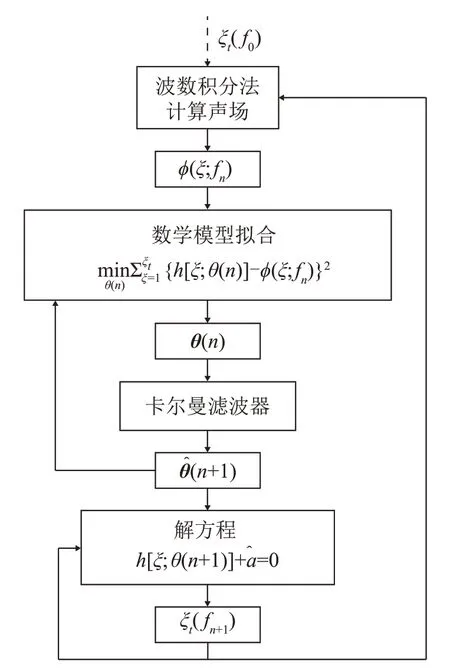
图5 截断波数自适应选取流程Fig.5 The flow chart of adaptive selcetion process of truncated wavenumber

(1) 初始截断波数ξt(f0)，ξt(f0)的取值可以较大，以保证声场计算精度。

(2) 利用波数积分法计算声场和ϕ(ξ;fn)。

(3) 利用式(11)中的数学模型对进行ϕ(ξ;fn)拟合，得到参数θ(n)。把上一次迭代自适应滤波器估计的参数作为求解此最优化问题的初值，以加快拟合速度。

(4) 把参数θ(n)输入卡尔曼滤波器，估计下一个频率的模型参数

(6) 返回步骤(2)计算下一个频率的声场。

2 仿真验证

计算图1所示海洋波导的波数域格林函数，并利用本文提出的方法选取积分截断波数，以验证本文提出方法的有效性。初始截断波数取值是ξt(f0) =5，计算频率范围是50～1 000 Hz。卡尔曼滤波器的参数如表1所示。

表1 卡尔曼滤波器参数的取值Table 1 Values of Kalman filter parameters

对精确度参数a取不同值、频率间隔Δf取不同值的情况进行试验。图6 是Δf分别为1、5 和10 Hz 时，a分别为3，4，5，6 的情况下，ϕ(ξt(f);f)随频率变化，其中ξt(f)为本文方法选取的截断波数。

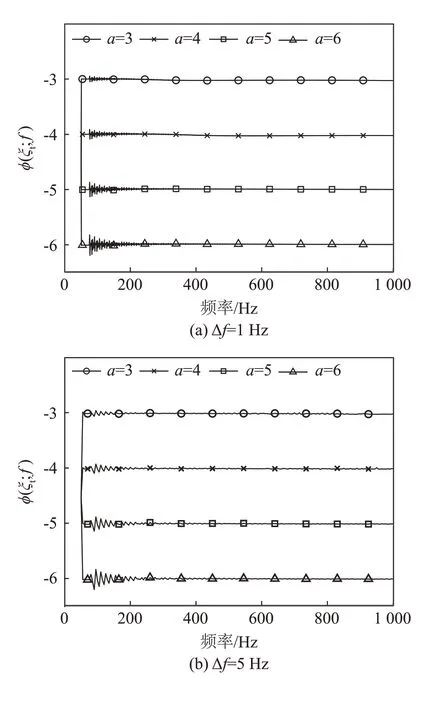
图6 采用本文方法计算声场时截断处波数域格林函数的对数幅值随频率变化图Fig.6 Logarithmic magnitude of Green's function in wavenumber domain at the truncation versus frequency when the method proposed in this paper is used for sound field calculation

图6中的结果表明在上述试验条件下，本文提出的方法都能自适应地选取积分截断波数，实现在期望的精确度附近进行积分截断。在较低频段，实际截断处幅值ϕ[ξt(f);f]会出现波动，随着频率的增大，波动逐渐减小。这是因为确定截断精确度a后，当频率较低时，ϕ(ξ;f)随频率f的变化比较剧烈，因而模型参数的预测误差比较大；当频率较高时，ϕ(ξ;f)随频率f的变化比较缓慢，因而模型参数的预测误差较小，截断精确度误差变小。

图6说明了本文提出的自适应截断波数选取方法能在宽带声场波数积分计算过程中，把截断处的格林函数幅值稳定地保持在某一个精度附近。作为对比，图7给出了当ξt取固定值时，声场计算过程中截断处波数域格林函数的对数幅值随频率变化。可以看出当ξt取固定值时，声场计算过程中截断精确度随频率的增大而不断提高。

图7 采用ξt取固定值法计算声场时截断处波数域格林函数的对数幅值随频率变化图Fig.7 Logarithmic magnitude of Green's function in wavenumber domain at the truncation versus frequency when the fixed ξt method is used for sound field calculation

为了评估本文方法对声场计算速度的影响，在其他条件都相同的情况下，分别利用常用的ξt取固定值的方法和本文提出的自适应截断波数选取方法，计算50～1 000 Hz 宽带声场100 次，对比两种方法的平均用时。为了量化对比两种方法的积分截断精确度，计算宽带平均精确度amean：

其中：n为频率序号，N为频点个数，ϕ[ξt(fn);fn]为截断处格林函数对数幅值。

表2 和表3 分别为采用ξt取固定值的方法和本文提出方法进行声场计算的平均用时和带宽平均精确度。在平均用时比较接近的情况下(如表2中ξt=1.1，1.2，表3中a=3,4,5,6的情况)，采用本文方法选取截断波数能获得更高的宽带平均精确度；在宽带平均精确度比较接近的情况下(如表2中ξt=2.0和表3 中a=3 的情况)，采用本文方法选取截断波数所需平均时间更少。这是因为ξt取固定值的方法无法兼顾低频精确度和高频计算量。由图7可知，当ξt取固定值1.1或1.2时，虽然计算量不大，但低频声场计算的积分截断精确度太低，导致宽带平均精确度较低；而当ξt取固定值2.0或3.0时，虽然声场计算整体的积分截断精度足够高，但高频声场计算量较大，导致计算的平均用时较大。本文提出的方法在宽带声场计算过程中，积分截断精确度可稳定地维持在某一个值上，在保证了低频积分截断精确度的同时不会给高频声场计算增加不必要的计算量。

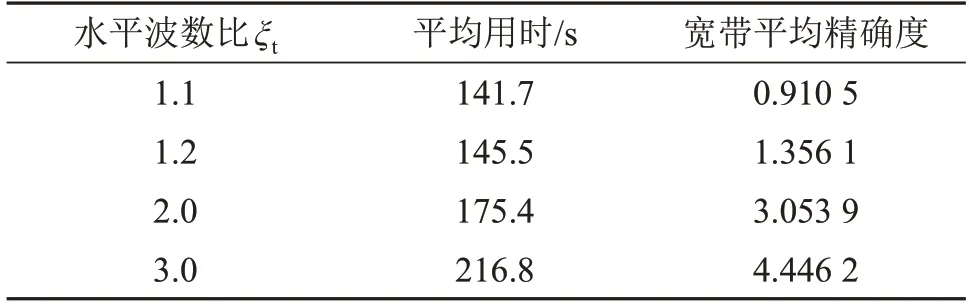
表2 水平波数比取固定值方法声场计算平均用时和宽带平均精确度Table 2 Average time and broadband average accuracy of sound field calculation with the fixed horizontal wavenumber ratio method

表3 本文提出的方法声场计算平均用时和宽带平均精确度Table 3 Average time and broadband average accuracy of sound field calculation with the method proposed in this paper

3 结 论

由于频率、介质类型、波导参数、声源与接收点的相对深度等参数会对波数域格林函数的衰减特性产生很大的影响，在采用波数积分法计算不同海洋波导的声场时需要选取不同的积分截断波数。针对波数积分宽带声场计算过程中，现有积分截断波数选取方法所存在的问题，本文提出一种应用于流体介质声场计算的积分截断波数的自适应选取方法。利用数学模型拟合波数域格林函数的衰减特性，根据已计算的波数域格林函数预测下一频率的波数域格林函数的衰减特性，然后估计出积分截断波数。仿真试验结果表明，本文提出的方法实现了在给定的精确度附近进行积分截断，在保证积分精确度的同时不会引入太多额外的计算量。

本文提出的波数积分法截断波数自适应选取方法除了可以用于宽带多频点的声场计算外，还可以拓展到其他参数渐变的声场计算场景。

本文关注的是各层都是流体介质的海洋波导的情况，当海底是弹性介质或波导中包含冰盖层时，波数域格林函数的衰减特性会有所变化。能否把本文提出的截断波数自适应选取方法，应用到包含弹性介质的海洋波导的波数积分声场计算，有待进一步研究。

构造函数模型拟合图3中的曲线，可以得到给定精确度时截断波数随频率变化的经验公式，这可能是解决此问题的另一种思路。但图3中的曲线会随波导参数的改变而改变，如何建立曲线参数与波导参数之间的关系有待深入研究。