地震灾害下城市电网关键单元防护资源配置
2022-06-29赵旭东龚华栋张树财
张 宁, 赵旭东, 龚华栋, 张树财
(陆军工程大学 国防工程学院,江苏 南京 210007)
城市生命线网络是重要经济目标防护的重要组成部分,一般包括城市电网、天然气网络、通信网络、交通运输网络和城市供水网络等[1]。这些网络对保障城市正常运行和居民生产、生活起着至关重要的作用。城市生命线网络是近些年研究的热点,学者们基于易损性[2-3]、风险[4-7]和韧性[8-10]等概念开展了大量的研究。这些研究为防护资源配置的研究奠定了基础。
在自然灾害背景下,地震灾害以其频发性较高、危害性大而著称,对生命线网络造成的“风险”是一种典型的“概率性风险”。“概率性风险”是由巧合或机会所引起的一种不确定性风险。城市电网在生命线网络中处于能源供应地位,其余生命线网络对城市电网均有不同程度的依赖。如:交通运输网络离开电力供应会很快陷于瘫痪境地,通信网络若无电力供应无法正常完成信息的传输与交换,供水网络若无电力支持泵站无法展开工作。因此,研究地震灾害下城市电网的防护资源配置具有重要的现实意义。
目前,地震灾害下防护资源优化配置方法主要有以下4类:(1)确定性收益分析方法[11];(2)随机性收益分析方法[12-13];(3)多属性效用分析方法[14-15];(4)优化模型方法[16-19]。尽管前3种方法一定程度上能为灾前防护资源配置提供决策分析,但是随着城市生命线网络规模的快速扩张,级联复杂不断提高,对其进行防护形成数量巨大的资源配置方案,前3种方法在寻求最优解上存在着困难,而优化模型方法则能很好地解决这一问题。
本文防护资源的配置研究基于“风险”[5]的概念,将背包问题的决策模型应用到城市生命线网络资源分配上,提出概率性风险下防护资源配置的一种优化模型,指导地震灾害下城市电网灾前防护资源配置。对于防护方所投入的防护资源,一般指用于目标防护的资金、材料、物资等消耗资源。为了方便量化,将投入的防护资源无量纲化。防护资源的投入目标是在有限的防护资源条件下实现灾害袭击毁伤后果的最小化。
1 概率性风险下防护资源优化配置模型
1.1 风险定义
近年来复杂网络理论作为有效的工具被应用于城市生命线网络的研究中,生命线中的关键单元、单元之间的连线分别表述为网络中的节点和边。节点i的风险被定义为[5]
Ri=ai×pi(di)×Ci
(1)
式中:Ri表示节点i的风险;ai表示节点i受到袭击的概率;pi(di)表示节点i的易损性,即完成一次成功袭击的可能性;Ci表示节点i遭受一次成功袭击的后果。
当ai=1时,节点遭受攻击的风险被定义为固有风险,并表示为
IRi=pi(di)×Ci
(2)
节点易损性pi(di)表示一次袭击成功的可能性,一般随着防护资源投入数量的增加而逐渐降低(p′(di)<0),且降低的速率逐渐变慢(p″(di)>0)[20]。Guan等[21]回顾了几种易损性非线性连续衰减公式,并提出了非连续易损性衰减公式。Golany等[22]假设随着防护资源投入的增加,易损性呈线性衰减规律。一般情况下,非线性易损性相较于线性易损性更符合工程实际情况,线性、非线性衰减公式会影响每个节点需要投放的资源量,但对所提模型方法本身没有影响。本文采用Golany等的假设,因为本文是探讨地震灾害背景下防护资源如何配置的问题,并非深入探究易损性与防护资源的精确数量关系。这样的线性假设能满足研究的需要,同时可以简化计算量。
本文基于易损性线性衰减规律,将易损性定义为
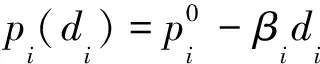
(3)

此时,节点i的固有风险表示为

(4)
当节点i未分配到防护资源时,此时初始固有风险表示为

(5)
对于节点风险后果Ci,学者们多基于复杂网络理论中网络连通性[23]、连接密度[24]、节点介数[25]等概念描述。这种方式较好地借助了复杂网络理论将网络节点毁伤带来的系统价值表述出来,但存在着不足,在上述假设中要求城市电网始终沿着最短路径传输,这是不符合实际情况的。单纯地考虑网络节点毁伤带来的系统价值影响是不全面的。本文考虑电网潮流特点的网络效能E[26],定义节点风险后果Ci。
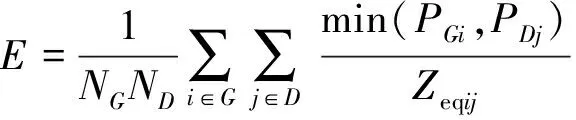
(6)
式中:E表示网络效能,G表示源点,D表示负荷点,NG表示源点数量,ND表示负荷点数量,min(PGi,PDj)表示源点i和负荷点j有功功率的较小值(即“发电-负荷”节点对之间可以传输的最大功率),Zeqij表示源点-负荷点之间的等值阻抗,即传输距离。
等值阻抗Zeqij,即电气距离,表示单位电流i从发电节点流入,从负荷节点j流出时,节点对(i,j)之间的电压差值。节点阻抗矩阵为
VB=ZBIB
(7)
式中:VB表示节点电压的列向量,IB表示节点电流的列向量。
如果单位电流从源点i流入,从负荷节点j流出(Ii=1,Ij=-1),那么任意节点k的电压可计算为
Vk=Zki-Zkj
(8)
式中:Zki、Zkj分别为节点对(k,i)、(k,j)的互阻抗。
基于等值阻抗,考虑了电气特性,更能从功能上反映电网输电效能。E0表示初始完好状态的城市电网效能,Ei表示网络中节点i破坏后的城市电网效能,故节点i的网络效能变化量为
ΔEi=E0-Ei
(9)
将ΔEi作归一化处理,得到网络节点i的破坏后果Ci为
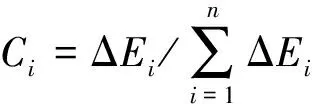
(10)
1.2 概率性风险下防护资源配置优化理论
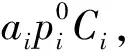
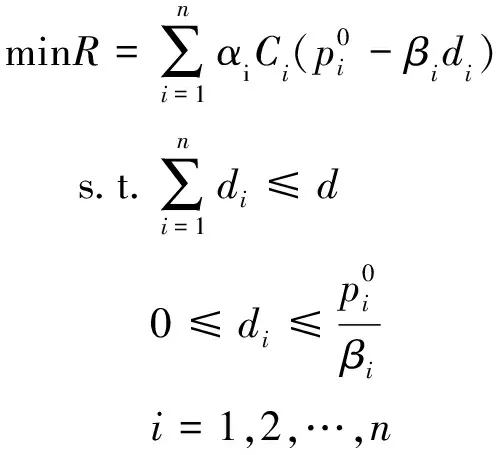
(11)


(12)
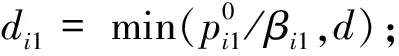
上述分配方案是参数化的,即它为所有可能的防护资源总量提供了概率性风险的最优解。此外,这个最优解是稳健的,因为只要不违反可用性约束,对资源可用量更改之前已经投放的资源仍然是最佳分配方案的一部分。尤其是对该问题进行敏感性分析时,如果有额外的防护资源可以利用,它将全部分配给那些尚未得到完全防护的节点中排名最高的节点。最后,如果增加新的节点,则可以通过调整式(12)的排名和相应的目标函数,就可以获得最佳分配方案,不会改变之前节点的内部排名,也不会发生排名逆转。
2 案例分析
本文采用IEEE-30总线网络验证上述提出的理论。IEEE-30总线网络拓扑图如图1所示,包括6个发电机(编号为1,2,3,4,5,6),其参数见表1,4个变比可调的变压器支路可作为变电站(编号为7,8,9,10),其参数见表2,此系统中还有21个负载节点,其中节点1为平衡节点。
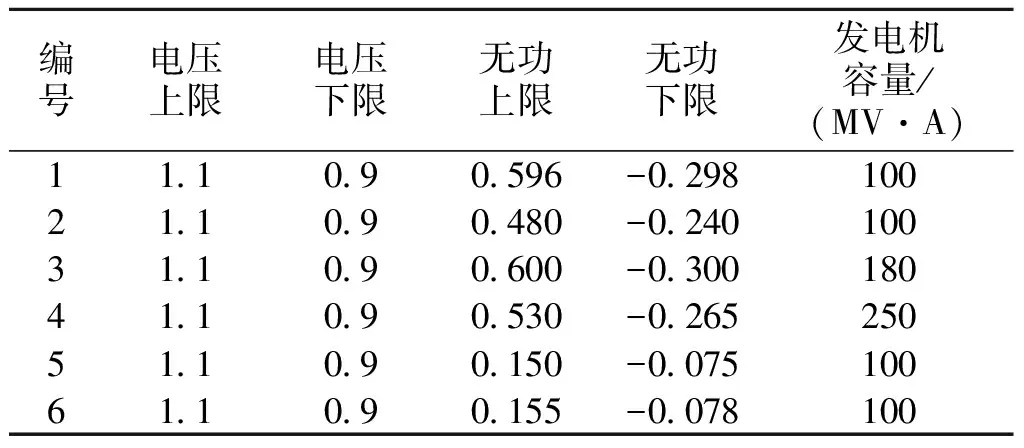
表1 IEEE30-bus network发电机参数

表2 IEEE30-bus network 变压器支路参数
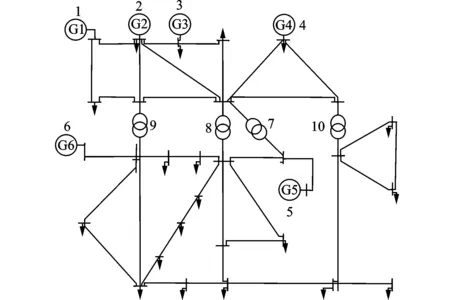
图1 IEEE-30电力网络节点图
根据式(10)计算出IEEE-30总线网络中10个关键节点的破坏后果(重要度)Ci如图2所示。
本文研究目的是分配有限的防护资源尽可能降低城市电网的预期损失,因此防护资源优先防护关键节点,如发电厂、大型变电站、中转站等,至于小型变电站、负载节点、输电线路,可以考虑在一定半径范围安排抢修救援队,这不在本文研究范围。
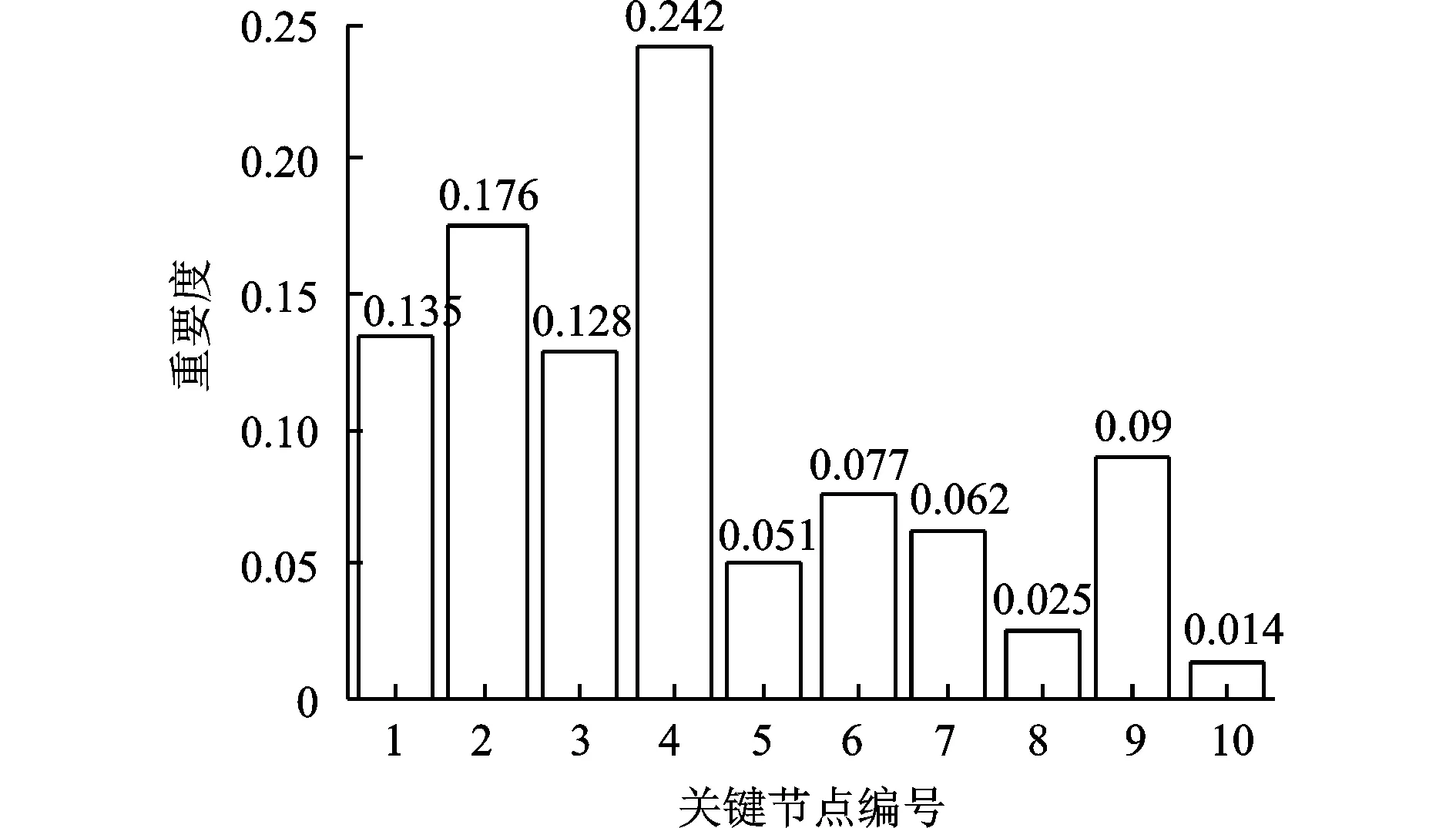
图2 IEEE-30关键节点重要度
根据概率性风险下防护资源优化理论,需要确定地震灾害下城市电网关键节点的易损性和重要度。对城市电网各个设施单元的毁伤概率确定如下:
因着海兰抱病,今日并未去大殿行哭礼,青樱见她立在门外,便道:“这样夜了怎么还来?着了风寒更不好了,快进来罢。”
(1)确定城市电网所处区域,结合《中国地震动参数区划图》、《中国地震烈度区划图》,确定网络可能遭受的地震动参数,本文取峰值地面加速度(PGA)表征地区地震强度大小。对于可液化或滑坡地区,采用峰值地面位移(PGD)和PGA共同决定。

假设IEEE-30总线网络所在地区的场景地震设防烈度为Ⅶ,地震动峰值加速度分区与地震基本烈度对照表如表3所示,基于最大程度保证安全的原则,地震烈度Ⅶ不变的情况下,峰值地面加速度(PGA)采用0.15g。查阅FEMA开发的HAZUS-MR4技术手册,对电网设施单元分级如表4所示。

表3 地震动峰值加速度分区与地震基本烈度对照表
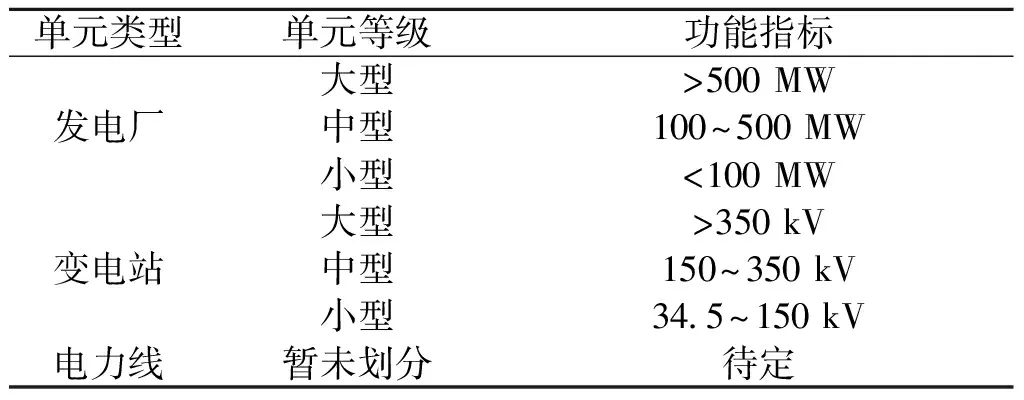
表4 基于易损性的电网设施单元分级
根据电网易损性单元分级,发电厂均为中型等级,变电站均为小型等级,电网设施达到轻微损伤状态即丧失部分功能,无法正常完成工作。地震灾害的随机破坏,导致电网设施单元遭受毁伤的概率不同。查阅HAZUS-MR4技术手册,地震灾害下中型发电厂、小型变电站的易损性曲线图分别如图3、图4所示。
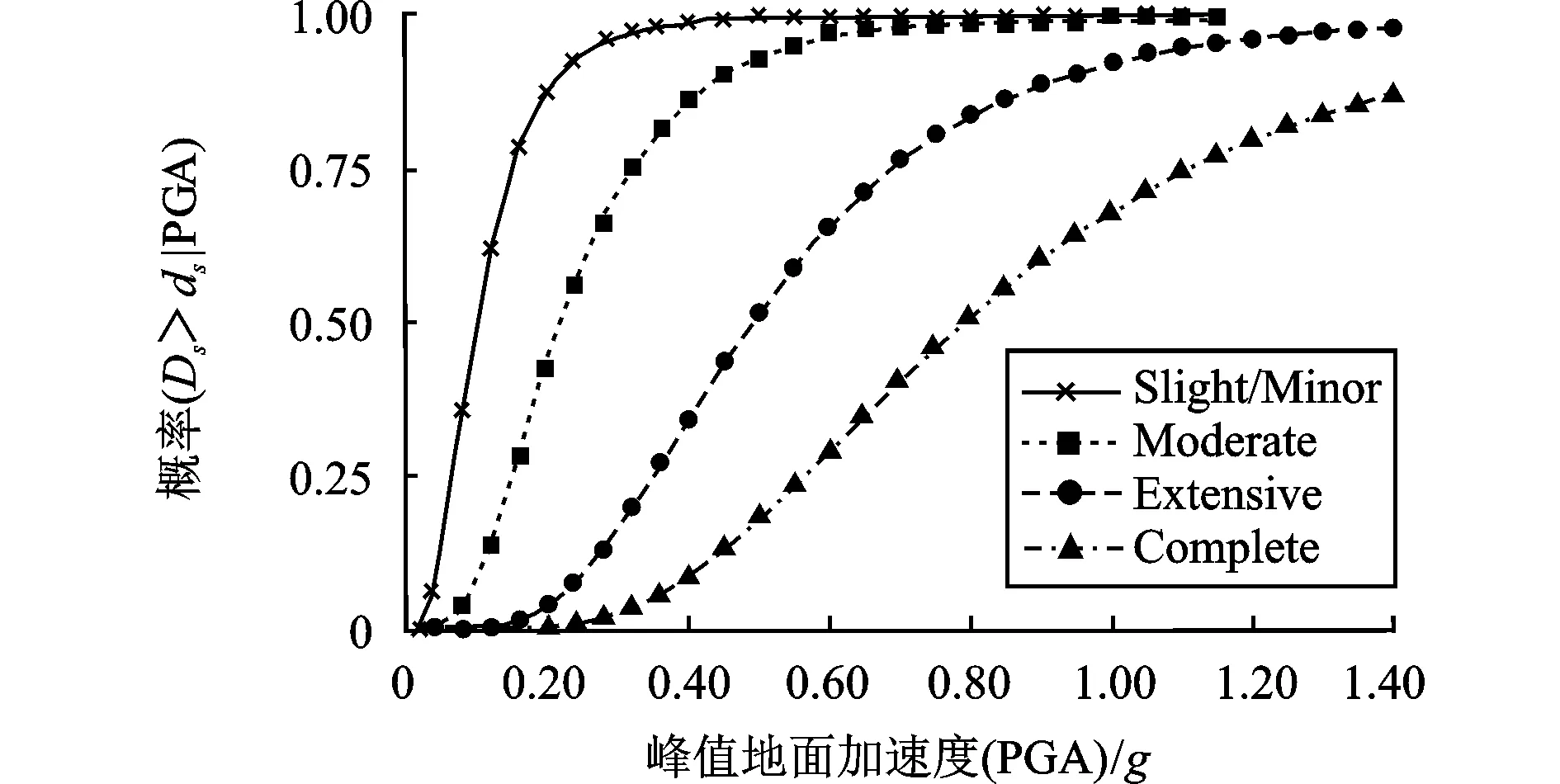
图3 未锚固组件的中型/大型发电设施组件的易损性曲线图
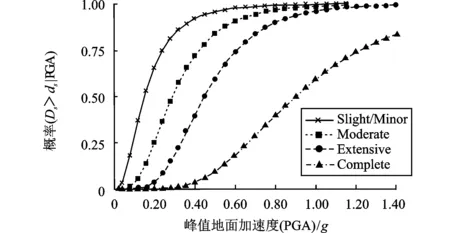
图4 小型变电站组件地震易损性曲线图
在PGA=0.15g不变的情况下,发电厂达到轻微损伤状态(初始易损性)的概率为0.76,变电站达到轻微损伤状态(初始易损性)的概率为0.53。由于保密的原因,电网关键节点真实的防护因子无法获得,设置关键节点的防护因子βi如表5所示,具体城市电网的关键设施单元可根据实际防护情况确定防护因子。
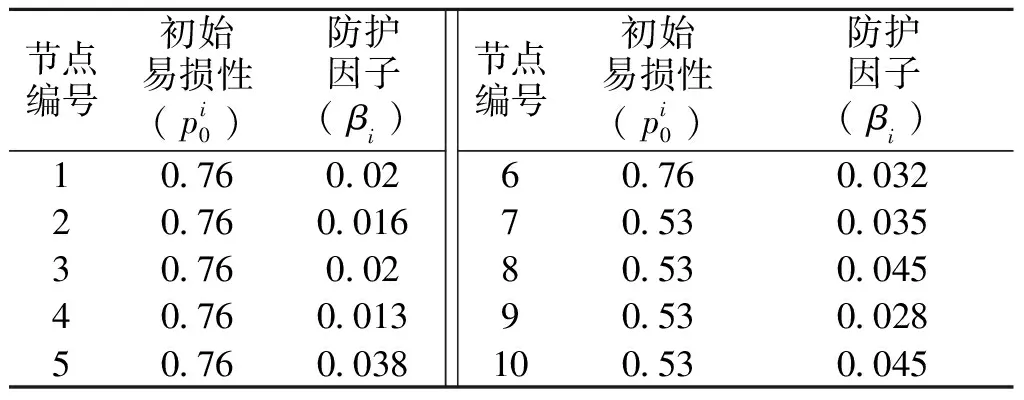
表5 关键节点易损性评价参数

表6 关键节点初始固有风险
排名靠前的关键节点得到完全保护之后,剩余的防护资源分配到接下来的关键节点,如图5所示。经计算,当防护资源总量d=283.34时,电网的关键节点得到完全防护。这可以避免前期防护资源过多的投入,当d=200,d=250,d=283.34时,分别计算总体风险R如图6所示。

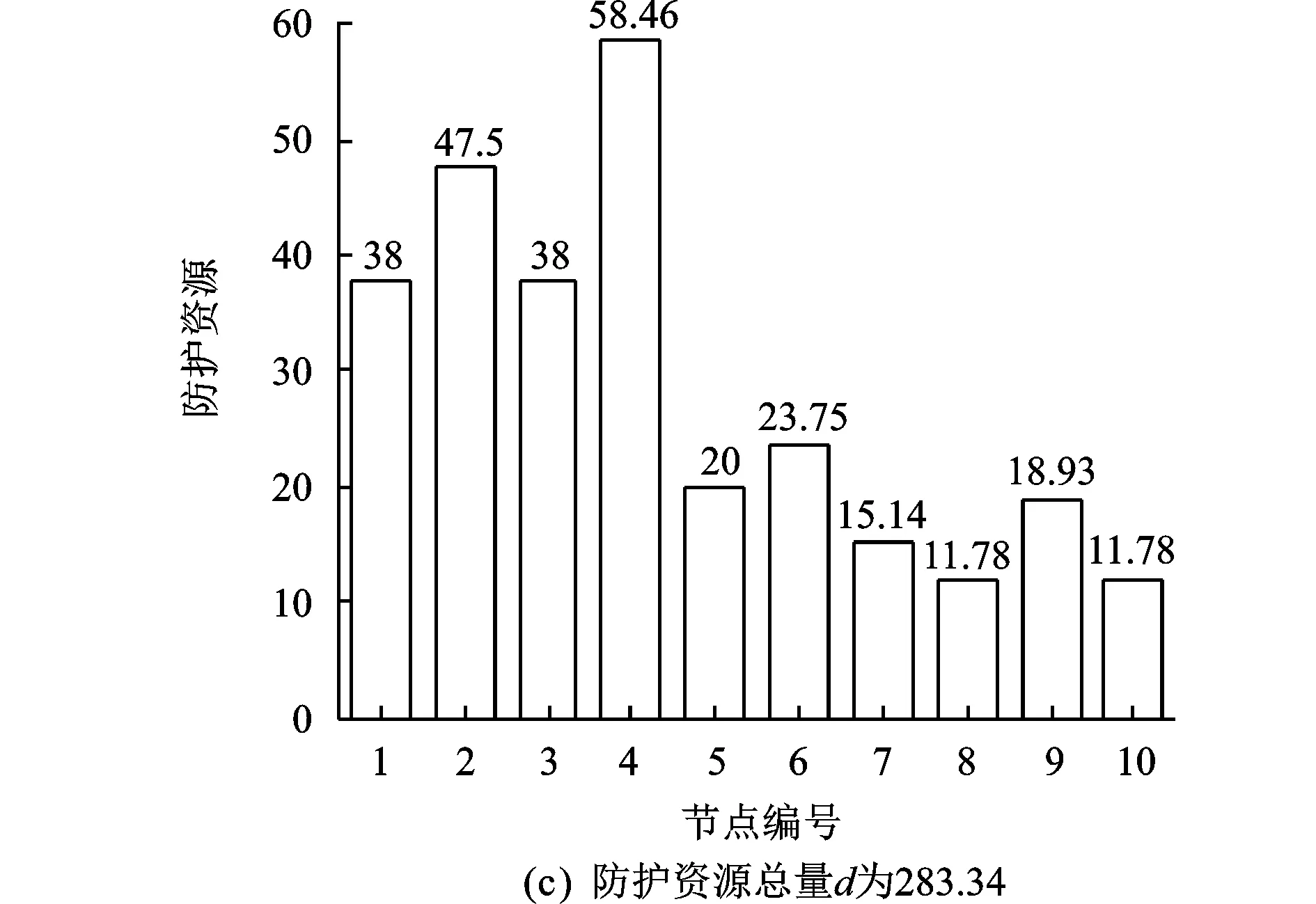
图5 关键节点防护资源分配量

图6 关键节点总体风险随防护资源总量变化趋势图
若电网新增一个发电厂,编号为节点11,其初始固有风险值介于节点3和节点6之间,表6中节点3之后的排名发生变化,但节点11的增加不改变节点3及其之前排名节点的防护资源分配量。
关键节点4的防护因子β4从0.005增加到0.02时,投入节点4的防护资源逐渐减少,防护资源被更多地投放到其他关键节点上,更多的关键节点得到防护(图7),网络的总体风险随着β4的增大也在逐渐减小(图8)。
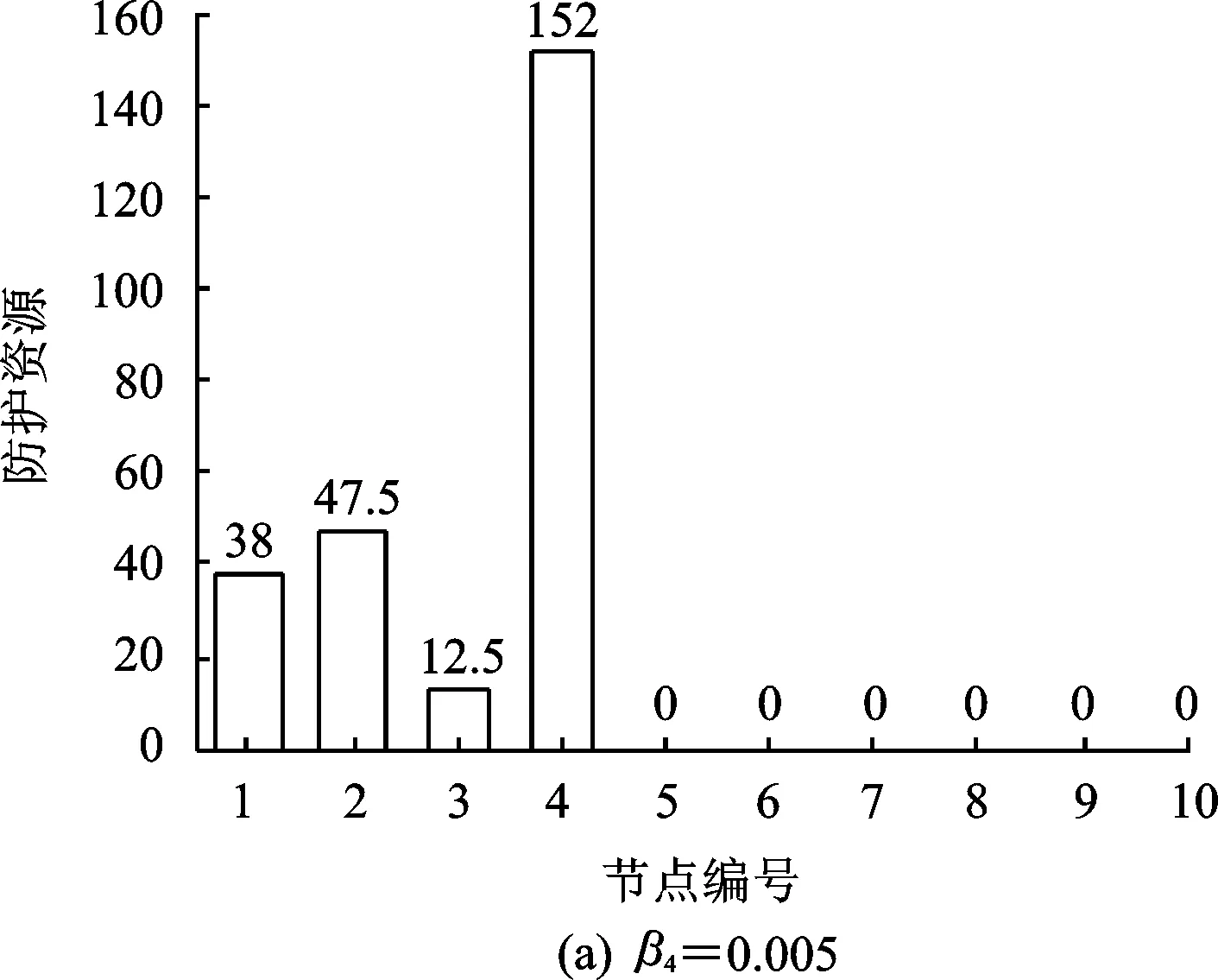
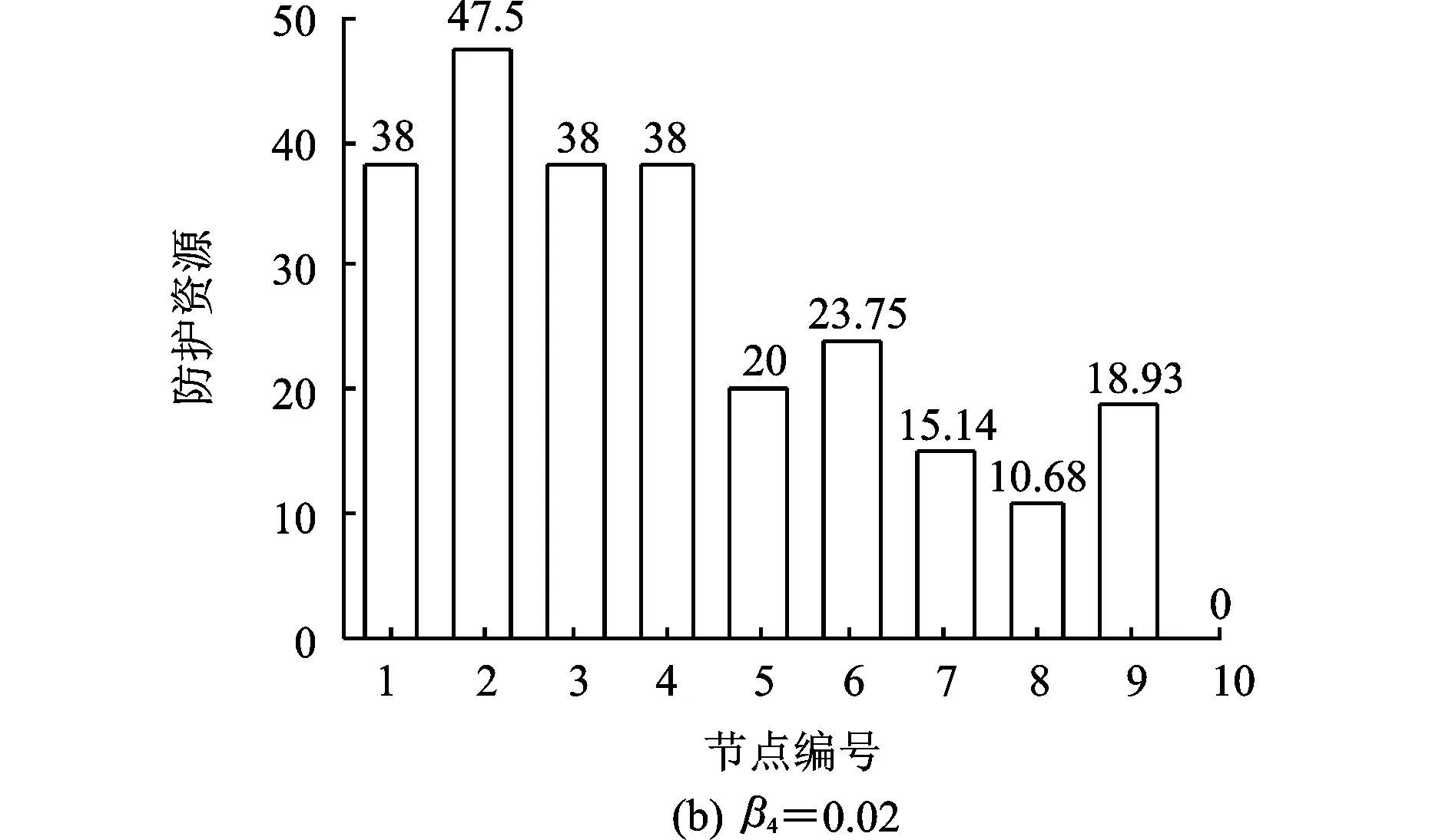
图7 随β4变化的防护资源分配量(设定防护资源总量d为250)

图8 关键节点总体风险随β4变化趋势图
3 结论
本文提出了城市电网在概率性风险下防护资源的最优分配策略。在概率性风险下,防护方必须重点关注初始固有风险最大的关键节点,将防护资源投入节点得到完全防护,然后再关注初始固有风险次大的节点,直到资源耗尽。
从防护方管理者的角度来看,概率性风险下的分配标准是尽可能增加每单位防护资源的效果,概率性风险下能产生最大影响效果的节点往往可以得到完全防护。
地震灾害背景下降低城市电网总体风险有以下途径:
(1)适当增加防护资源总量可以降低网络的总体风险,防护资源的增加量存在上限,过多地投入会造成防护资源的浪费和前期防护成本的增加。
(2)降低关键节点的易损性或增大排名靠前的关键节点的防护因子。在城市电网的前期规划中,如采取锚固、变电站地下化等措施,可以降低关键设施节点的易损性,增加电网的抗震安全性。
