基于误差交叉耦合的多电磁铁悬浮系统滑模协同控制

孙友刚 ，徐俊起 ，贺祯宇 ，李丰荥 ，陈 琛 ，林国斌

（1.同济大学铁道与城市轨道交通研究院，上海 201804；2.同济大学国家磁浮交通工程技术研究中心，上海201804；3.同济大学磁浮技术铁路行业重点实验室，上海 201804）

磁浮列车具有低噪音、优异爬坡能力、高转弯性能、无污染和高安全性等优点，正快速成为国内外的一种新型轨道交通方式[1-4].电磁悬浮（electro magnetic suspension, EMS）型磁浮列车依靠悬浮电磁铁与轨道之间的吸引力使列车与轨道保持大约8～10 mm的间隙，从而实现无接触运行.磁浮列车悬浮是通过悬浮架固接的多个悬浮电磁铁共同支撑完成.通过悬浮架的机械结构可以实现左右两侧解耦，但同一侧的电磁铁因为刚性连接，存在较强的机械耦合关系.当一个电磁铁动态发生变化会引起相邻的电磁铁动态也发生变化，即耦合扰动效应.目前，磁浮列车的各个电磁铁控制模块单独设计，互相之间没有通讯和协调，无法主动处理耦合扰动效应.而悬浮过程中不可避免的扰动会导致各悬浮间隙动态不同步，容易降低悬浮性能甚至引起悬浮失效.

因为系统的开环不稳定、强非线性和参数不确定等特征，磁浮列车的悬浮控制算法一直是研究热点和挑战.早期的研究为了方便控制器的设计，忽略多个电磁铁线圈悬浮时相互之间的耦合作用，可将悬浮控制对象简化为单点悬浮系统：蒋启龙等[5]早在20世纪90年代就利用80C196单片机实现了悬浮系统PID数字控制；龙志强等[6]利用反馈线性化技术将系统的输入状态线性化，设计出PI控制器和对应的非线性补偿器；汪科任等[7]基于全状态反馈增益矩阵设计了线性控制器来解决低轨道梁刚度下稳定悬浮，但多个悬浮电磁铁之间并没有考虑误差补偿和协同.近年来，人们开始对多点悬浮控制进行深入研究；王亮等[8]在建立了多点悬浮模型的基础上，通过矩阵变换将系统的电磁力和运动状态进行空间解耦，并根据稳定性能要求和极点配置理论设计了一个闭环控制系统，但仍采用经典控制理论；李奇南等[9]以钢板动力学模型为基础，通过引入气隙交叉耦合控制来改善动态气隙同步性能；徐俊起等[10]基于多点悬浮模型提出基于交叉耦合控制算法，对系统的输出误差进行补偿，但稳定性分析时对系统进行了线性化处理；赵伟等[11]针对磁浮列车多点悬浮系统设计了无模型自适应模块化控制方法.虽然协同控制在磁浮列车领域研究较少，但已经在机器人[12]、风电机组[13]和分布式电动汽车[14-15]等领域取得成功应用.

本文针对多电磁铁悬浮系统展开误差交叉耦合的滑模协同控制方法研究.首先建立了多电磁铁悬浮系统动力学模型，并分析其耦合特性.然后设计未知动态和干扰的状态观测器；接着根据跟踪误差和同步误差提出交叉耦合的滑模面，并设计包含耦合协同补偿项的滑模协同控制律；在不做任何线性化的前提下，通过Lyapunov方法分析闭环系统的稳定性；最后通过实验验证所提方法的有效性.

1 多电磁铁悬浮系统特性分析

1.1 系统描述

磁浮列车的每节车厢由5个悬浮架组成，悬浮架左右解耦.通常悬浮架由电磁铁悬浮模块、极板、防滚梁、防滚吊杆、托臂等组成，当电磁铁通电后，利用电磁吸引力无接触地悬浮在轨道上，便实现了悬浮运行.悬浮架的同一侧由4个电磁铁线圈（2个电磁铁悬浮模块）构成，如图1所示.

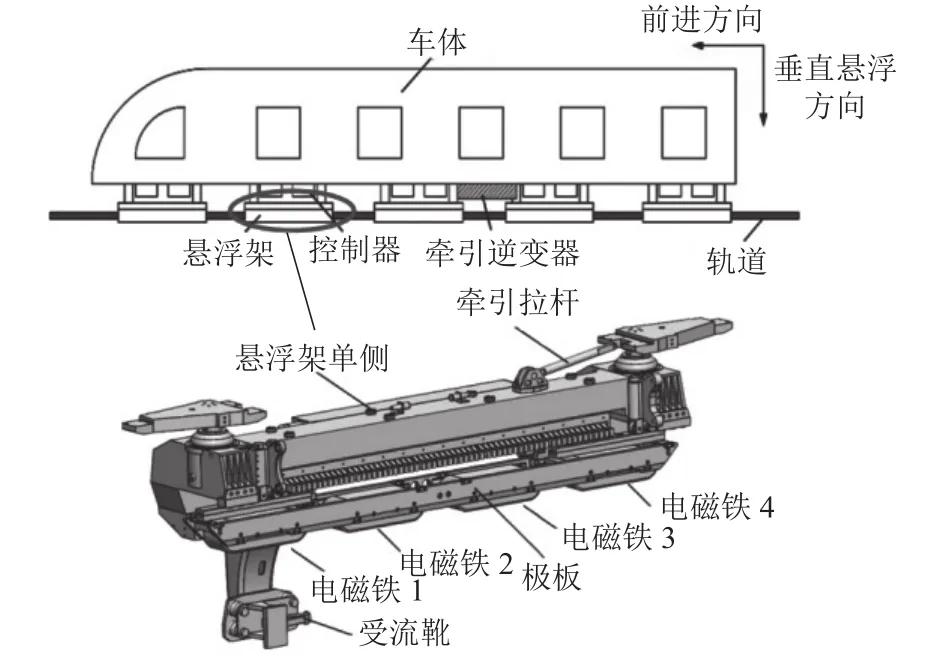
图1 悬浮架同侧多电磁铁悬浮系统Fig.1 Multi-electromagnet suspension system on the same side of suspension frame

1.2 多电磁铁悬浮系统动力学建模及分析

为分析多电磁铁的协调作用，将悬浮架同侧的两个电磁铁悬浮模块（4个电磁铁线圈）进行建模并分别协同，如图2所示.图中：Fm1和Fm2为两个电磁铁悬浮模块的电磁力； δm1和 δm2为两个电磁铁悬浮模块的悬浮间隙；a和 β 分别为质心O点到模块中点距离和极板旋转的角度.4个电磁铁之间采用刚性极板连接[16]，因此悬浮架同一侧的多电磁铁悬浮系统可视为杆结构，并在两端固定两个电磁铁悬浮模块，需要对2个控制回路的悬浮间隙进行协同.

图2 多电磁铁悬浮系统动力学模型Fig.2 Dynamic model of multi-electromagnet suspension system

根据电磁学理论，系统的电磁力[17]可表示为

式中： μ0、A分别为空气磁导率和磁极面积；im1和im2为两个电磁铁悬浮模块需要协同的控制电流；t为时间；

假设电磁铁线圈匝数Nm1、Nm2、Nm3和Nm4相同，线圈匝数都为 0.5Nm即Nm1=Nm2=Nm3=Nm4=0.5Nm，因此电磁力改写为

如图2所示，因为悬浮间隙空间很小，转角也很小，转角可近似为

中心竖直方向上的位移为

旋转引起的位移大小为

由式（3）～（5）得

忽略极板质量，系统竖直方向上的合力大小为

式中：ms为一个电磁铁悬浮模块的质量；g为重力加速度.

绕质心O点的转矩大小为

得到质心的动力学方程为

定义等效转动质量mβ=I/a2，式（10）可转化为

由式（9）和式（11）可得

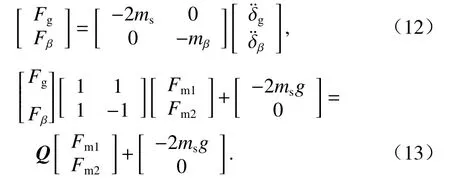
由式（7）和（11）可得

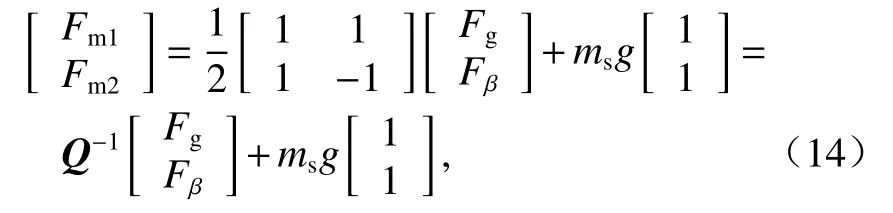
代入式（12）得到

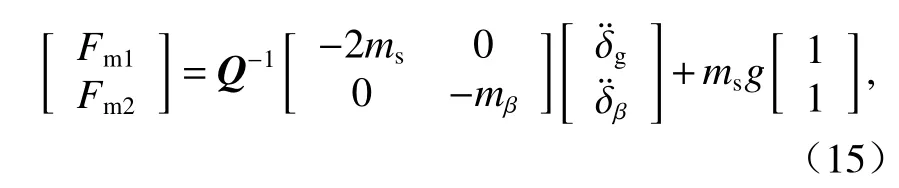
再代入式（6）可得到

于是

代入Q，并合并同类项可得

通过以上分析可知，悬浮架同一侧多电磁铁悬浮系统的耦合关系可由不同电磁铁悬浮模块的悬浮间隙和电磁力表征.从动力学模型式（18）的电磁铁和加速度变换矩阵可以看出，变换矩阵为非对角阵，因此可以判断多电磁铁悬浮系统中不同悬浮间隙和系统输出之间存在耦合.

1.3 控制目标

因为斩波器的应用，可以设计电流为控制量的反馈控制器，通过控制两个电磁铁模块中的电流实现 多电磁铁线圈的同步协调悬浮.当4个电磁铁线圈（两个电磁铁控制模块）的悬浮间隙和速度相同时，多电磁铁悬浮系统z方向上的垂向平移运动是最主要运动.因此，这里做适当简化，将考虑未知干扰的多电磁铁悬浮系统的同步协调控制问题转化为由具有非线性电磁力的两个电磁铁模块的悬浮间隙和速度同步控制问题.考虑未建模动态和未知扰动，状态方程可以简化为

式中：xi1=δmi，xi2=，其中i=1,2 ；和为控制器设计时磁悬浮系统参数的名义值，=g，为虚拟控制量，真实控制量di(t)/ms， ΔDmi和 ΔBmi为未建模动态，di(t) 为未知干扰力.

设目标悬浮间隙为xd=δd，定义两个电磁铁模块的跟踪误差和间隙同步误差分别为

式中：e1(t) 为电磁铁模块1的悬浮气隙跟踪误差；e2(t)为电磁铁模块2的悬浮气隙跟踪误差；x11为电磁铁模块1的悬浮气隙；x21为电磁铁模块2的悬浮气隙； εs为误差交叉耦合下的间隙同步误差.

在对每个电磁铁模块单独进行控制时，控制目标是使得e1(t) 、e2(t) 、 εs(t) 收敛于 0，即

2 基于误差交叉耦合的滑模控制器

2.1 干扰观测器

电磁悬浮控制的一大挑战为未建模动态和干扰Wi(t)难以实际测量.本节拟通过引入扰动观测器，利用方便测量的系统变量对Wi(t) 进行预测，从而实现对简化数学模型的补偿，观测值作为前馈项引入控制器中，降低未建模动态和干扰对悬浮稳定性的影响.

以电磁铁子模块的状态空间方程（19）为基础，通过控制输入ui(t) 和可测的悬浮间隙xi1对系统状态变量进行状态重构，实现间隙变化速度和未知干扰力的观测.

假设1假设未建模动态和干扰项的导数为有界函数即≤a.

设计干扰观测器为

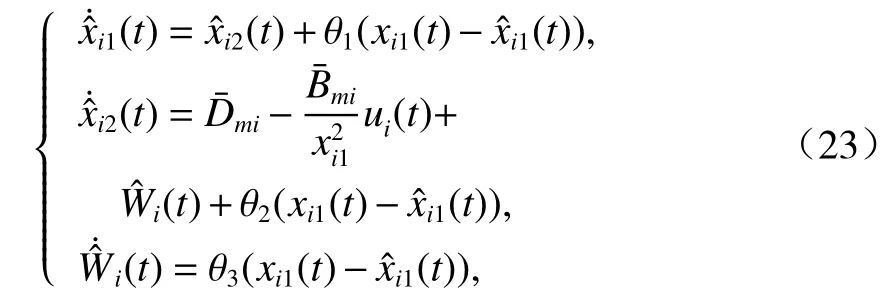
式中： θ1=r1/σ 、 θ2=r2/σ2、 θ3=r3/σ3， σ ＞0 ，r1、r2、r3均为大于 0 的实数， γ =[r1r2r3]T； σ 为决定着观测误差 γ 的收敛速度， σ 越小， γ 收敛速度越快，当 σ 减小至一定程度，观测误差趋近于0[15].

2.2 基于误差交叉耦合的滑模协同控制律设计

跟踪误差为

等式两边关于时间求导可得

对于磁浮列车而言，悬浮目标间隙xd一般为固定值，即.

设计系统的滑模面为

式中：si为悬浮控制器i的误差交叉耦合滑模面；c1和c2均为交叉耦合系数；k1和k2均为滑模系数，可以通过 Hurwitz 稳定性确定c1、c2、k1、k2系数的值[17].

如图3所示，设计滑模协同控制律为

图3 带观测器的滑模协同控制系统框图Fig.3 Block diagram of sliding mode cooperative control system with observer

式中：uieq(t) 和uisw(t) 分别为电磁铁模块i的等效控制律和切换控制律；uioh(t) 为耦合协同补偿项.

引入干扰观测器估计值，等效控制律可设计为

选取指数趋近律设计切换控制律如下：

式中： ξ1和 ξ2均为切换系数.

设计耦合协同补偿项为

等效控制律uieq(t) 为状态控制项，与模型参数和观测器估计值相关；耦合协同补偿项uioh(t) 与双电磁铁模块的间隙同步误差相关.若将c1和c2同时设置为0，则协同控制器将退化为单电磁铁控制器，将丢失间隙同步误差补偿的能力；切换控制律uisw(t) 作用是使得系统状态到达滑模面，但是 s gn(·) 会引入不连续控制量，引起系统振颤现象.

为了避免振颤现象，利用饱和函数代替sgn(·)函数，即

式中： φ0为边界层厚度，在边界层以内采用连续的状态反馈控制，避免了不连续开关特性.

3 稳定性分析

根据式（19）和（20）可得

对式（26）的两边关于时间求导可得

将饱和函数改进后的ui(t) 代入式（33）可得

定义Lyapunov候选函数为

显然V(si)≥0 ，且当且仅当si=0 时函数等于0.对式（35）两边关于时间求导得

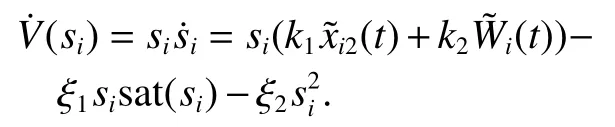
因为干扰观测器的误差趋近于0[15]，即可得

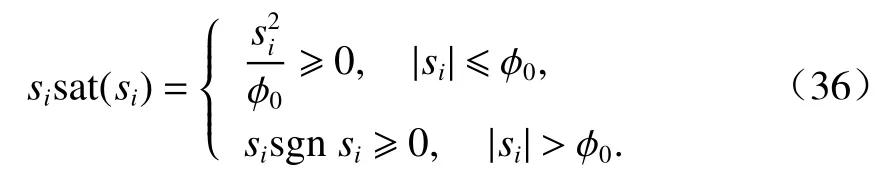
4 试验结果

为验证多电磁铁悬浮系统协同控制方法的有效性，建立如图4所示的单悬浮架试验平台.试验平台上由一个悬浮架、8个电磁铁线圈、4个空气弹簧、4个悬浮传感器和4个悬浮控制器组成.因为悬浮架左右模块结构上解耦，本实验仅利用左半侧进行悬浮实验.从图4可以看到左侧悬浮架的布置情况，由2个悬浮控制器、2个电磁铁模块（4个电磁铁线圈）和2个悬浮传感器组成.2个悬浮控制器之间采用CAN总线进行通信和误差交叉耦合，不需要重新设计控制板卡.悬浮架的系统参数如表1.

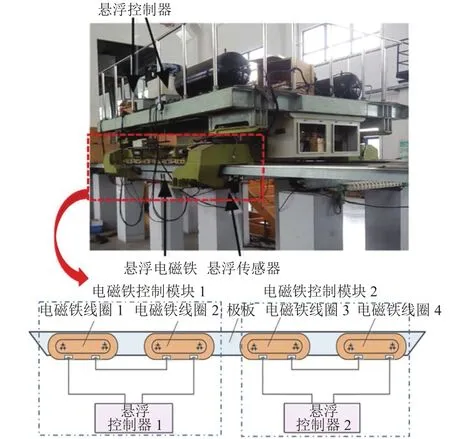
图4 带多电磁铁模块的悬浮架试验平台Fig.4 Suspension frame test platform with multi-electromagnet modules

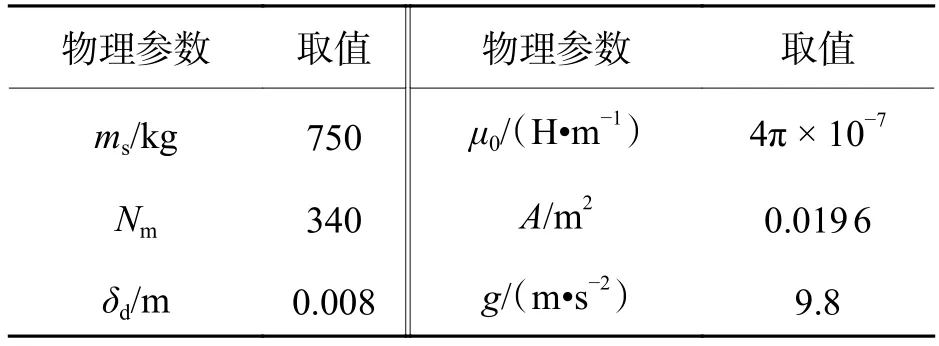
表1 磁悬浮系统参数Tab.1 Magnetic levitation system parameters

为了方便对比验证，分别采用本文提出的基于误差交叉耦合滑模的多点悬浮系统协同控制算法和未加协同控制的传统PID 控制算法进行综合抗干扰能力对比试验.传统PID控制器的控制参数分别选

取为kp=9500 ，ki=100 ，kd=370.而本文所提的协同控制器的参数如下：

为了对比协同控制的优越性，试验分两组进行：

第一组，悬浮架的4个空气弹簧保持未充气状态，采用独立的PID控制算法，数据采样频率为512 Hz.在悬浮点1对应的平台上方约1 m高的位置采用吊车吊起2个100 kg的载荷，在悬浮架实现静态稳定悬浮后，先放下第1个载荷，约7 s后再放下第2个载荷，从而进行力冲击试验.2个电磁铁悬浮模块的间隙波形和悬浮电流波形如图5、6所示.由图5可知：电磁铁悬浮模块1的间隙相对目标间隙的最大波动约为0.43 mm，电磁铁悬浮模块2的间隙最大波动约为0.03 mm.由图6可知：在冲击时悬浮电流波动最大的为电磁铁模块1，而模块2的电流波动不明显.

图5 悬浮间隙波动实验结果（PID控制器）Fig.5 Experimental results of suspension airgap fluctuation（PID controller）

图6 悬浮电流波动实验结果（PID控制器）Fig.6 Experimental results of suspension current fluctuation （PID controller）

第二组，悬浮架的4个空气弹簧保持未充气状态，采用加入误差交叉耦合的协同滑模控制律，工况和第一组完全相同来进行力冲击试验.2个电磁铁悬浮模块的间隙波形和悬浮电流如图7、8所示.电磁铁悬浮模块1的间隙相对目标间隙的最大波动约为0.262 mm，而电磁铁悬浮模块2的间隙波动最大约为0.238 mm.由图8可知，受到冲击时电磁铁悬浮模块1和模块2的悬浮电流最大波动几乎都是2 A左右.

图7 悬浮间隙波动实验结果（滑模协同控制）Fig.7 Experimental results of suspension airgap fluctuation（sliding mode cooperative control）

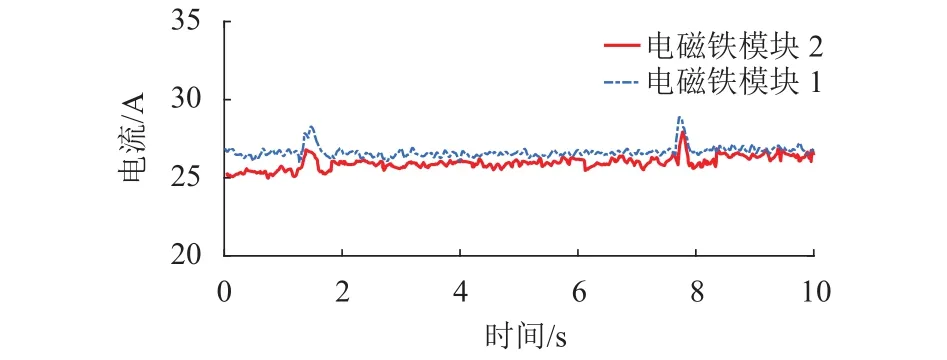
图8 悬浮电流波动实验结果（滑模协同控制）Fig.8 Experimental results of suspension current fluctuation （sliding mode cooperative control）

由实验结果可以看出：在没有施加协同控制时，在电磁铁模块1上方施加冲击力时，由于两个电磁铁模块之间没有协调补偿，两个悬浮间隙的差值较大（轮廓误差），最大的轮廓误差达到0.400 mm；而在协同控制下，电磁铁模块2对模块1的冲击干扰起到了补偿作用，可以看出电磁铁模块2的气隙误差较传统PID有所上升，而电磁铁模块1的气隙误差较传统PID时有所下降，峰值的轮廓误差为0.024 mm.可以看出，本文所提的协同控制方法利用气隙误差的交叉耦合使得电磁铁模块2有效补偿了模块1的气隙变化值，大大降低了轮廓误差.

加入本文所提出的滑模协同控制策略时，电磁铁模块1的间隙跟踪误差比未加协同控制策略时降低了约40%，大大降低了电磁铁模块1因发生较大波动而使该悬浮点滑撬触轨的可能.

5 结 论

本文针对中低速磁浮列车多电磁铁悬浮系统，提出了一种基于误差交叉耦合的滑模协同控制方法.分析了动力学模型并引入干扰观测器，通过设计协同控制器提高多电磁铁悬浮系统鲁棒性.

1） 通过动力学模型分析可知，电磁铁模块间的耦合效应是由变换矩阵为非对角阵引起；

2） 所设计的状态观测器不但能在线估计干扰力的大小还能估计间隙变化速度；

3） 所提出的滑模协同控制器能在理论上实现闭环系统的渐近稳定；

4） 通过实验结果可知，所提方法相比不施加协同的方法能降低模块1的跟踪误差达40%.显著减少了电磁铁之间的耦合扰动作用，增强综合抗干扰能力.