区间二型离散不确定模糊系统的滑模控制
2021-03-17钱厚宇周绍生
钱厚宇,周绍生
(杭州电子科技大学自动化学院,浙江 杭州 310018)
0 引 言
区间二型模糊系统不仅对不确定性具有更好的处理能力,同时也极大简化了计算复杂度[1]。另一方面,在诸多非线性控制方法中,滑模控制具有很好的鲁棒性,尤其在处理外部扰动、系统参数变化等方面,具有较好的研究应用价值[2]。在一类不确定离散线性系统中,文献[3]选择合适的结构参数用于滑模面,提出一种基于闭环输出反馈的滑模控制器,得到了较好的鲁棒性能。多年来,关于T-S模型不确定模糊系统的滑模控制研究一直备受关注。文献[4]给出滑模指数稳定的充分条件,并应用凸优化理论得到可行的滑模控制器;文献[5]采取量化反馈方法,确保了闭环系统的二次稳定,使得闭环状态到达滑模面。上述文献采用的都是常规二次Lyapunov函数方法,但对于更为一般的模糊系统,该方法往往难以适用,而分段二次Lyapunov函数恰好弥补了这一不足[6]。对于一类带有不确定性的一型T-S离散模糊系统,文献[7]采用分段二次Lyapunov函数分析滑模运动稳定性,提出了两种滑模控制器设计方法。本文针对一类带有不确定性的区间二型离散模糊系统展开进一步研究,将分段二次Lyapunov函数和凸优化理论应用于滑模运动稳定性分析,给出系统渐近稳定的充分条件,设计了一种输出反馈下的闭环系统滑模控制器。
1 系统描述
用IF-THEN模糊规则描述的区间二型离散不确定模糊系统如下:
(1)
系统(1)经单点模糊、乘积推理及加权去模糊化后,得到:
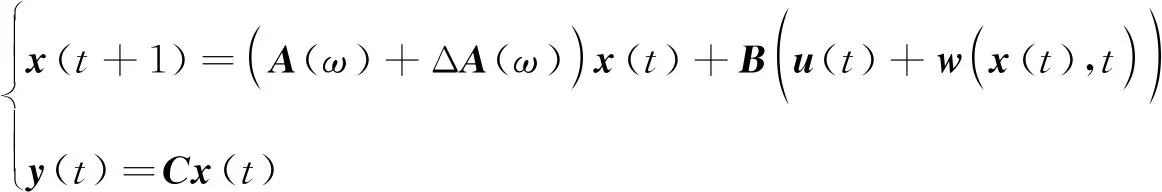
(2)
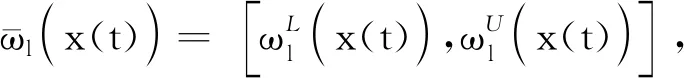
对于系统(2),利用可测得的系统输出y(t),本文将滑模面设计为:
s(t)=Ky(t)=KCx(t)=0
(3)
式中,K为滑模面增益。为了确定滑模面增益K并分析滑模运动稳定性,构造一个完整描述滑模运动的广义系统。
(4)
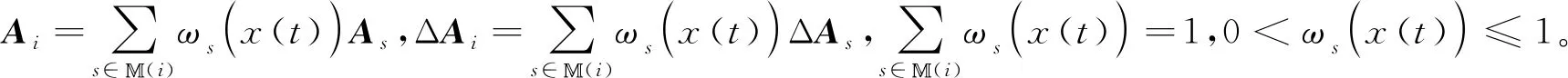

Px(t+1)=P(Ai+ΔAi)x(t)
(5)
结合滑模面(3)和式(5),得到完整的滑模运动方程:
(6)
(7)
为了便于后续研究分析,引入下列假设和引理。
假设1系统存在一个滑动块Ω,

(8)
式中,ε为一个已知的正常数。
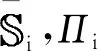
(9)
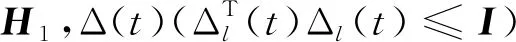
成立时,以下不等式成立。
(10)
2 主要结果
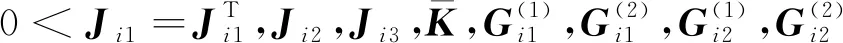
(11)
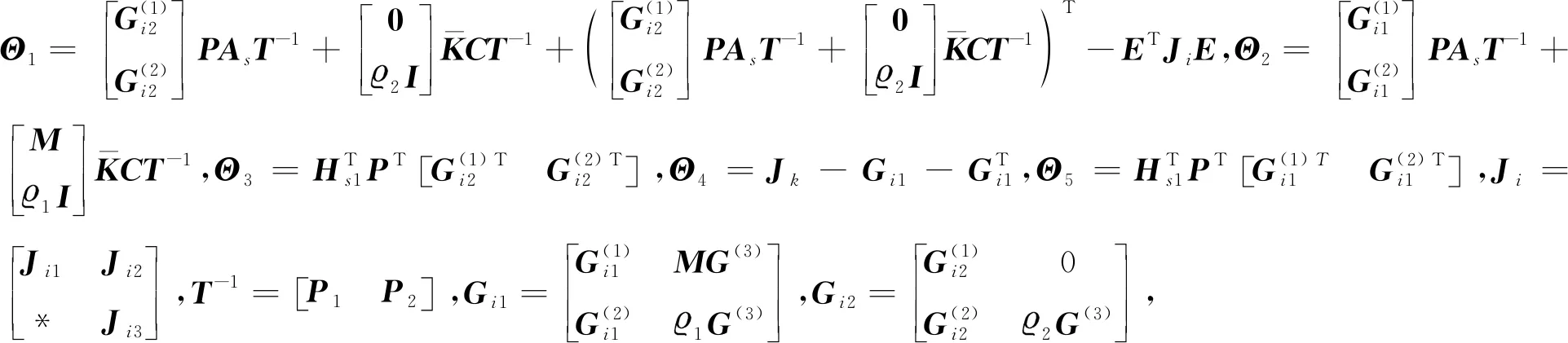
证明构造如下分段二次Lyapunov函数
(12)
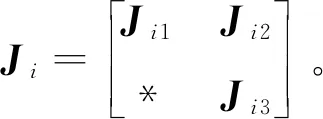
为了保证滑模动力学系统(7)渐近稳定,只需保证
(13)
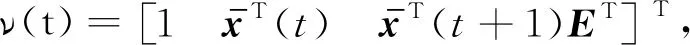
(14)
结合引理1,下列不等式可以推得不等式(14)
(15)
在系统(7)中,任意矩阵Gi为:
(16)
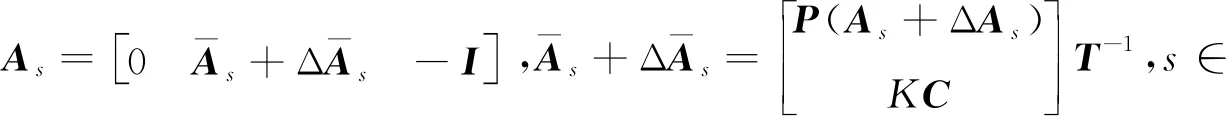

(17)
(18)
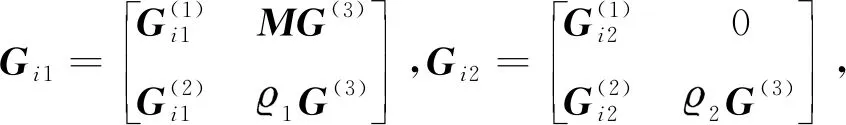
(19)
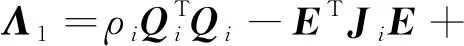
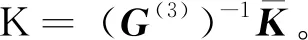
定理2对于满足假设1的系统(1)及其等效系统(2),保证输出反馈下的闭环系统状态可以在有限时间内到达滑模面(3)的控制器为
(20)
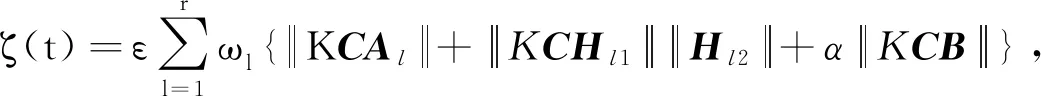
证明构造如下Lyapunov函数
(21)
另Δs(t)=s(t+1)-s(t),那么增量ΔV(t)为:
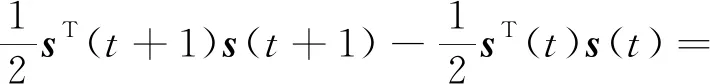
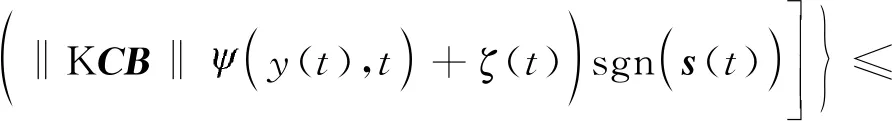
(σ+1)‖s(t)‖2-ζ(t)‖s(t)‖≤
(σ+1)‖s(t)‖2-ζ(t)‖s(t)‖=
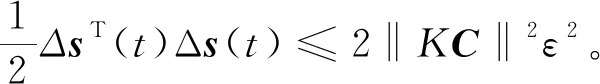
3 数例仿真
对于一种直升机俯仰角非线性数学模型[9],系统描述如下:
(22)
式中,x1,x2表示俯仰角(单位为rad)及其角速率(单位为rad/s),Iyy=0.028 3 kg·m2,mheli=0.994 1 kg,lcgx=0.013 4 m,lcgz=0.028 9 m,FvM=0.004 1 N·m/(rad/s),g=9.8100 m/s2[9]。采样周期T=1 s,对系统(22)进行线性离散模糊化,得到区间二型离散模糊系统:
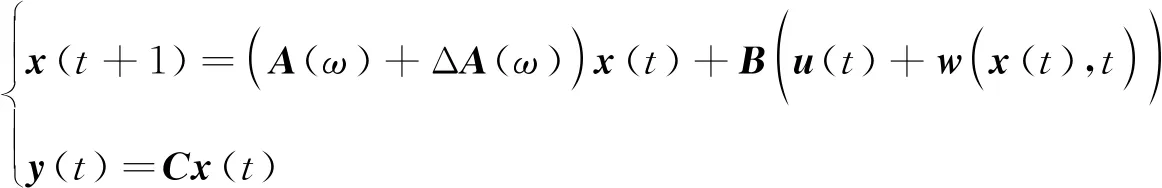
(23)
系统中,模糊规则个数r=2,各参数矩阵和区间二型隶属函数如下:
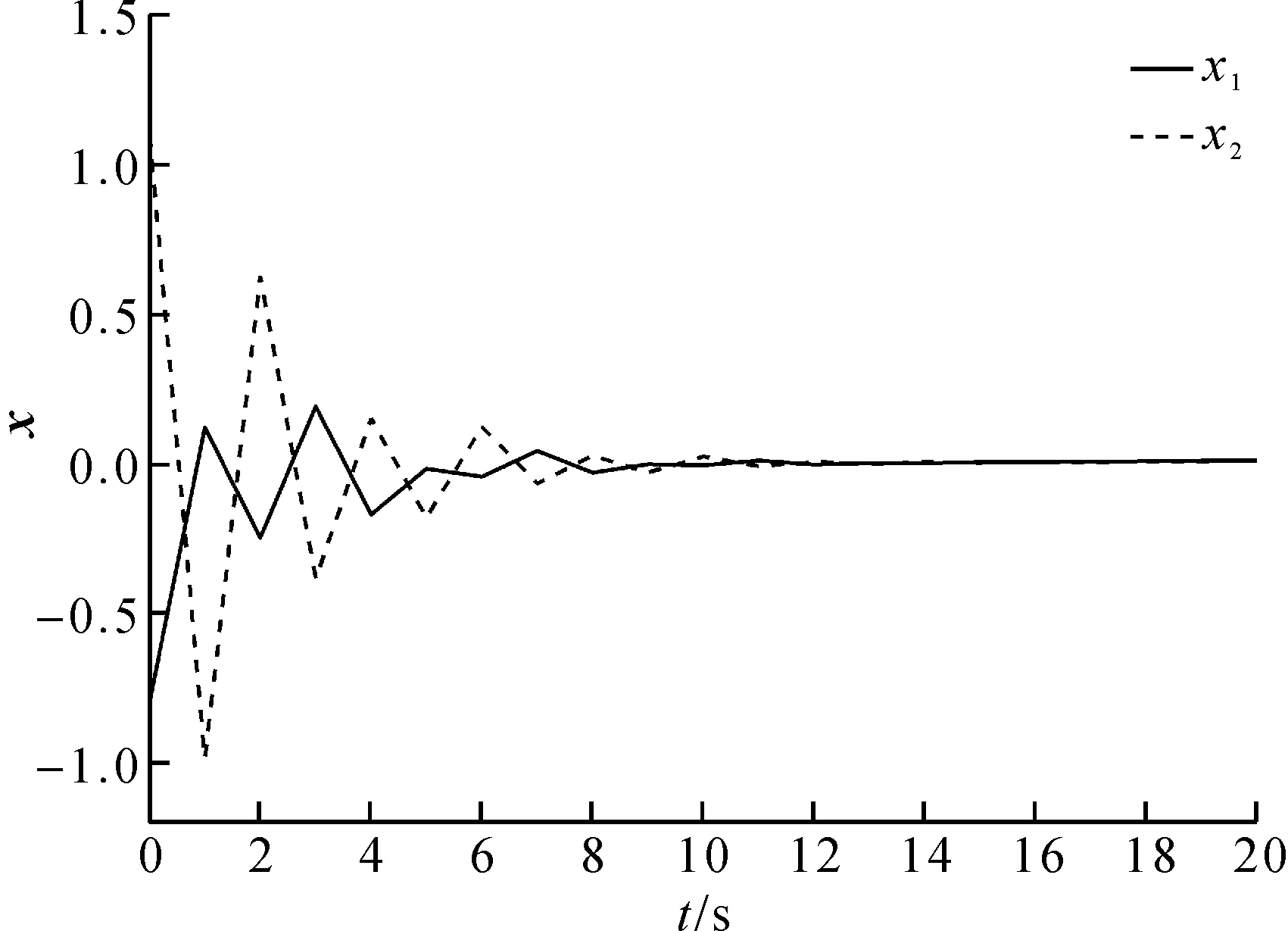
图1 闭环系统状态x响应轨线
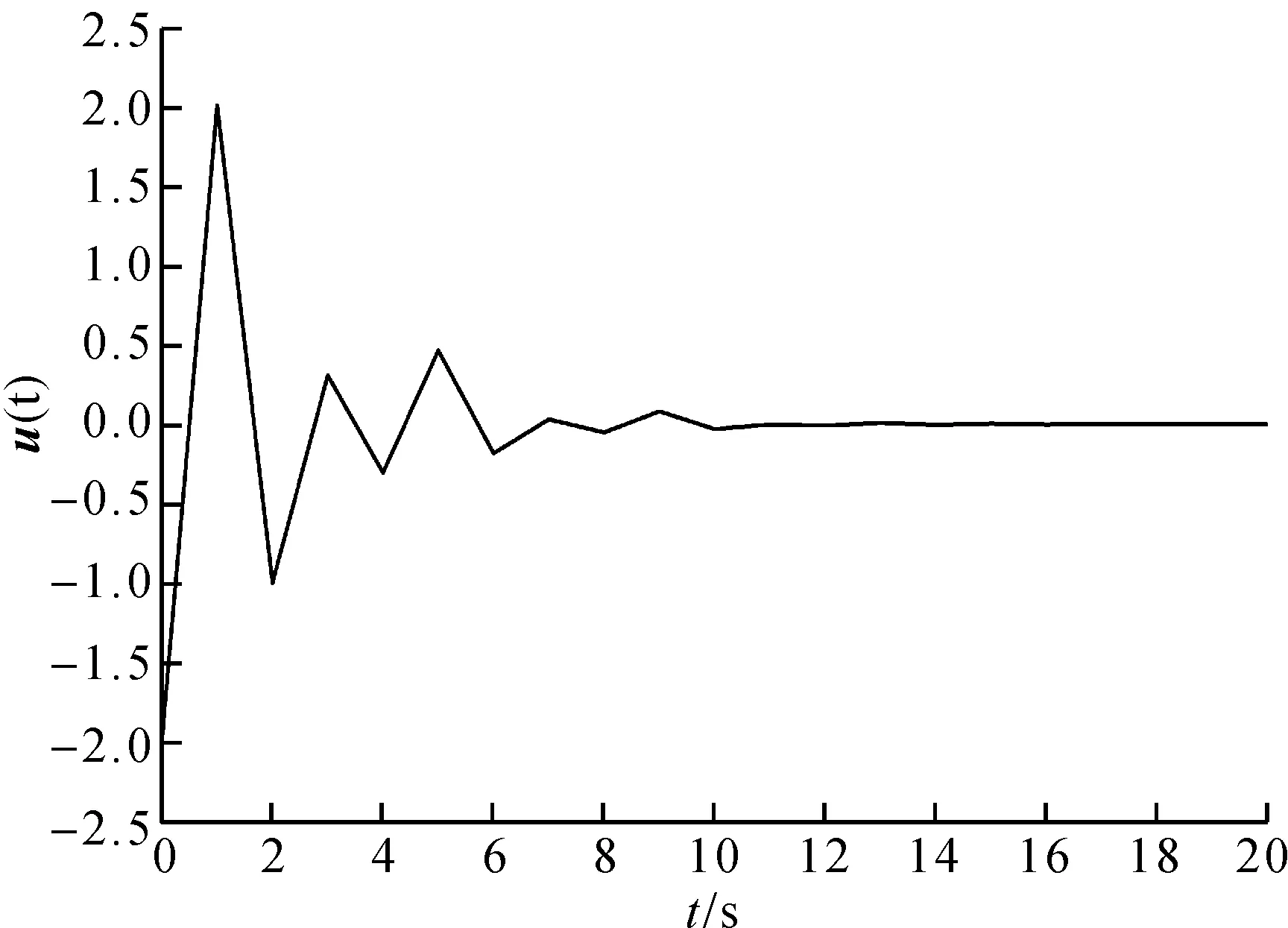
图2 滑模控制器u(t)的轨线
从图1和图2可以看出,较短时间内,在滑模控制器u(t)的作用下,闭环系统状态最终到达滑模面(3),从而验证了定理2中所构建的滑模控制器的有效性。
4 结束语
本文研究区间二型离散模糊系统的滑模运动稳定性和滑模控制器设计问题,通过线性变换建立广义系统模型,构造分段Lyapunov函数,设计的输出反馈滑模控制器消除了不确定性和输入扰动对系统的影响,使得该类系统具有较强的鲁棒性。但是,本文基于假设1所提出的滑模控制器,仅能保证滑模面在有限时间内局部的可达性,下一步将针对无假设情况下的自适应滑模控制器展开研究。
