气动翼对高速磁悬浮列车升力特性的影响

戴志远 ，李 田 ，张卫华 ，张继业

（西南交通大学牵引动力国家重点实验室，四川 成都 610031）

高速磁悬浮列车突破传统轮轨高速列车的速度极限，运行速度可达600 km/h以上，有望填补地面交通工具与航空的空白[1-2].2015年日本L0型磁浮列车的试验速度达到603 km/h[3]；2019年中车青岛四方时速600 km高速磁浮车下线[4]；2021年首套高速磁浮交通系统启用，2021年西南交通大学高温超导磁浮工程化样车及试验线的启用，都展现了高速磁悬浮列车研究取得的成果，也标志高速磁浮列车成为下一代轨道交通车辆的重点发展方向[5].

磁悬浮列车采用抱轨运行方式，车体与轨道梁之间存在较小间隙，该间隙内的流场对磁悬浮列车的悬浮特性、导向控制特性有显著影响.较之于轮轨接触高速列车，空气动力学效应对磁悬浮列车的制约更大[6-7].为此，国内外学者对磁浮列车的气动性能开展了大量研究，李人宪等[8]采用数值模拟的方法研究了横风作用下磁悬浮列车的气动力，并采用4种不同的悬浮间隙对比分析了其对磁悬浮列车气动载荷的影响；刘堂红等[9-10]以上海TR08型磁悬浮列车为基础研究了列车头型纵向剖面及横向剖面外形对列车气动阻力的影响，得到了气动阻力较小的磁悬浮列车头型；Sun等[11]基于交叉验证Kriging代理模型对磁悬浮列车的头车流线型部位进行优化，以整车阻力及头车升力为优化目标，得到了综合气动性能较好的头型.毕海权等[12-13]通过数值模拟计算研究了自然风对磁悬浮列车气动升力、侧滚力矩和偏转力矩等气动载荷的影响，可为磁悬浮列车的运行安全性提供指导与建议.现有研究主要集中在中低速磁浮气动性能分析及优化减阻方面，较少有关于高速磁悬浮列车气动特性的研究.但现有研究成果对高速磁悬浮列车的发展有重要的指导意义，也揭示了高速磁浮列车与轮轨高速列车气动性能的异同，气动升力特性便是显著差异之一，文献[7]的研究也表明磁悬浮列车高速运行时受到较大气动升力作用，尤其是尾车向上的气动升力较大.过大的气动升力易使悬浮性能恶化，甚至导致悬浮控制系统失效，影响高速磁浮列车的乘坐舒适性与运行安全性.因此，高速磁浮列车尾车的气动升力特性亟待改善，但目前少有对高速磁浮列车气动升力特性的研究.本文以某高速磁悬浮列车为研究对象，对其气动性能进行分析，并基于加装气动翼改善尾车升力特性，研究了气动翼角度、数量对尾车升力特性的影响，获得了较好的方案，可为高速磁悬浮列车的设计与优化提供参考.

1 计算模型与网格

1.1 数值计算模型

采用头车、一节中间车和尾车组成的三车编组高速磁悬浮列车进行数值模拟计算，列车与轨道梁的几何模型如图1（a）所示.磁悬浮列车的特征高度H为4 160 mm，车长约为19.5H.列车与轨道梁之间的悬浮高度为150 mm，导向间隙为10 mm，在导向间隙周围建立加密区（Refinebox1）以提高网格质量以更准确地求解流场，如图1（b）所示.图1（c）为数值模拟计算的计算区域.

图1（c）中：原点位于头车鼻尖，同时位于计算区域的纵向中心截面，在列车周围建立两个加密区（Refinebox2、Refinebox3）以提高列车附近网格质量.列车前方区域边界设置为压力远场条件，马赫数为 0.343，合116.6 m/s，即 420 km/h；列车后方区域边界设置为压力出口条件，出口压力为0；计算区域的侧面及顶面设置为对称边界条件，地面及轨道梁设置为滑移壁面，滑移速度为116.6 m/s.

图1 数值计算模型Fig.1 Numerical simulation models

在多种数值求解模型中，雷诺平均方法（Navier-Stokes）被广泛应用于高速列车外流场的数值模拟中，且k-ωshear stress transport（SST）湍流模型能更好地求解列车表面附面层流动[14].在列车空气动力学中，列车运行速度大于0.3倍当地声速后必须考虑空气的可压缩性[15].因此，采用可压缩的k-ωSST两方程模型及semi-implicit method for pressure-linked equations（SIMPLE）算法进行压力及流场求解，控制方程采用二阶迎风离散格式.

1.2 网格独立性与风洞试验验证

以 3个基础尺寸（1 000、850 mm和700 mm）生成网格Mesh 1、Mesh 2和Mesh 3，网格数量分别为2 190万、2 671万、3 364万，对3套网格进行计算，验证网格尺寸对计算结果的影响.3套网格的边界层参数相同，第1层厚度为0.01 mm，增长比为1.2，总层数为18层，能够保证整车的无量纲化壁面距离y+ 在1附近，满足所采用的湍流模型的要求.研究所采用的3车编组高速磁悬浮列车已开展风洞试验[7]，风洞试验的来流速度为70 m/s，雷诺数为2.8 × 106，采用同样的来流速度进行数值模拟计算，并与风洞试验数据进行对比.

采用无量纲压力系数对比数值计算结果和风洞试验数据，压力系数为

式中：P为压力；ρ为空气密度；u为列车运行速度.

图2为数值模拟及风洞试验得到的磁悬浮列车在y= 0的压力系数Cp.图中：Exp表示风洞试验数据.

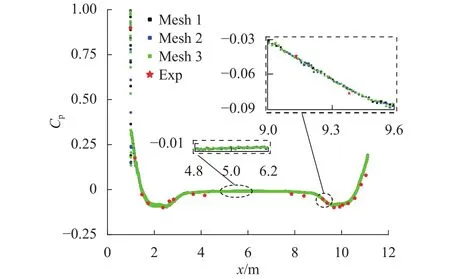
图2 y = 0截面压力系数分布Fig.2 Pressure coefficient distribution at plane y = 0

由图2可知：3套网格之间的压力系数分布几乎没有差异，说明网格数量达到2 200万附近后对数值模拟计算结果基本没有影响；同时，数值模拟计算得到的鼻尖驻点压力系数基本为1，且列车表面压力与风洞试验得到的列车表面压力变化趋势一致，对应点的相对误差较小，验证了数值模拟结果的准确性.以上计算结果说明本文采用的网格尺寸、数学模型及边界条件能够较准确地对高速磁悬浮列车进行气动性能数值模拟.此外，数值模拟计算精度与网格数量呈正相关，也即网格越精细、数量越多，理论上数值计算结果越准确.虽计算结果在网格数量达到2 200万附近后基本稳定，但为进一步保证数值模拟精度，可选取网格量稍多的网格进行计算，而Mesh 3网格数量过多，会延长数值求解的时间，降低计算效率.因此，综合计算精度和计算效率的因素，本文选取Mesh 2进行后续计算，Mesh 2部分网格如图3所示.

图3 列车周围网格及边界层网格Fig.3 Cells around the maglev trian and boundary layer

2 计算结果

2.1 气动翼角度对列车气动性能的影响

对原始高速磁悬浮列车进行数值模拟计算，根据计算结果确定尾车负压区位置，在负压区起始位置安装气动翼，共 5 种角度，分别为 5.0°、10.0°、12.5°、15.0°、17.5°，气动翼参数及安装位置如图4所示.

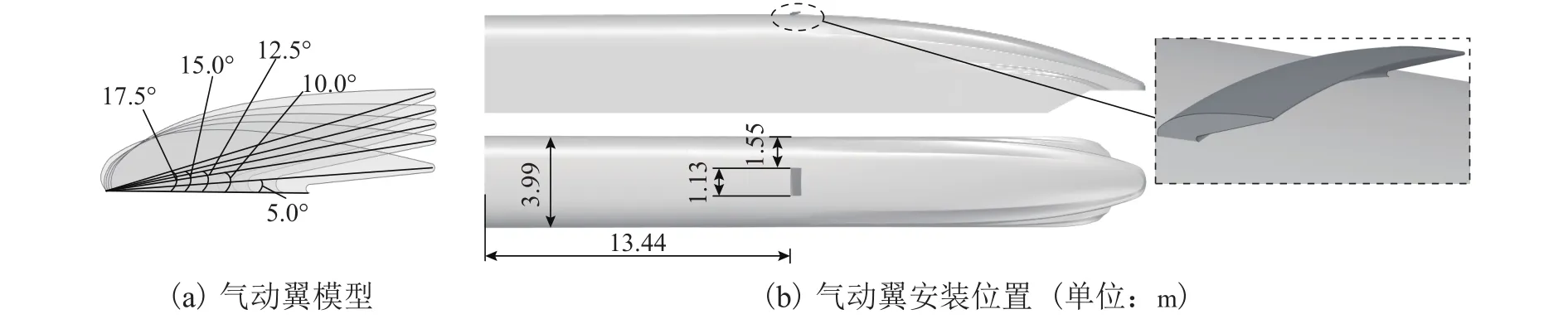
图4 气动翼模型及位置Fig.4 Model and location of the aerodynamic wing

高速磁悬浮列车的气动阻力系数Cd和气动升力系数Cl分别为

式中：Fd为气动阻力；Fl为气动升力；A为列车的迎风面积，取12.5 m2.

提取安装有不同气动翼的磁悬浮列车头车、中间车及尾车的气动力系数，如表1所示.表中：CdH、CdM、CdT和CdW分别为头车、中间车、尾车车体和气动翼的气动阻力系数（其中：CdT为不包含气动翼尾车的气动阻力系数；CdTT为包含气动翼的尾车的气动阻力系数）；Cl的命名方式同气动阻力系数.由表1可知：5种气动翼磁悬浮列车的头车、中间车气动力系数都与原始列车相同，说明安装在尾车的气动翼对头车及中间车的气动力及周围流场基本没有影响；CdT不随气动翼角度的改变而变化，气动翼自身的气动阻力系数随角度的增加而增大，从而尾车及整车气动阻力随气动翼角度增加略有增大；17.5° 气动翼磁悬浮列车整车的气动阻力系数最大，约比原始列车增加1.5%；气动翼自身升力随角度的增加逐渐减小，对尾车升力影响较大，使车体升力变化较复杂.随着气动翼角度的增加，尾车升力呈现先减小后增大的变化趋势，在气动翼角度为12.5° 时最小，与原始磁悬浮列车相比气动升力系数减小3.9%.

表1 列车及气动翼的气动力系数Tab.1 Aerodynamic force coefficient of the maglev trian and aerodynamic wings

为进一步分析气动翼对磁悬浮列车气动升力的影响，提取3种气动翼磁悬浮列车的尾车表面压力及气动翼周围流场压力分布，如图5所示.

图5 尾车表面压力系数及气动翼周围流场压力系数分布Fig.5 Pressure coefficient distribution of the tail car and the pressure distribution around aerodynamic wings

安装有不同角度气动翼的尾车表面压力分布规律相似，尾车车身流线型起始位置至司机室视窗基本被负压覆盖，气动翼也正是安装在负压区的起始位置.由司机室视窗向鼻尖方向列车表面压力逐渐升高，至尾车鼻尖处压力达到最大.对于气动翼，其迎风侧存在较大幅值的正压，而上表面产生了较大的负压，该负压是空气流经气动翼上方时流速增加引起的.气流流过气动翼后在气动翼的后方产生了涡，漩涡中心位置负压较大，漩涡后方气流紊乱使得气动翼后方空气流速有所下降，负压减小.由图5（b）也可看出：涡随着气动翼角度的增大逐渐后移，影响范围也逐渐扩大.在距离气动翼较远位置，其尾流对流场的影响减弱，气流速度逐步回升，尾车流线型区域的负压又重新集结.

为进一步量化尾车表面压力及升力随气动翼角度变化的规律，提取y= 0截面尾车及气动翼的表面压力系数，如图6所示.由图6（a）可得到：气动翼下表面的负压随角度的增加而增大，上表面迎风侧压力随角度增加由负压逐渐增大变为正压，上表面背风侧的负压也随气动翼角度的增加而增大.由于翼型倾角较小，其表面压力分布基本可以表征其在竖直方向的受力情况，气动翼上下表面所围成的积分面积可以反映气动升力变化规律，图6（a）中5.0° 气动翼上、下表面所围成的积分面积最大，随着角度的增加面积逐渐减小，17.5° 气动翼的最小，因此气动翼的气动升力也随角度的增加而减小，与表1中的结论一致.

气动翼安装在流线型区域的起始位置，该区域基本与水平面平行，采用与气动翼类似的分析方法，与Cp= 0所围成的积分面积可以表征尾车车体在气动翼附近的气动升力变化规律.由图6（b）可以看出：各工况在x= 62.5 m和x= 72.5 m附近的表面压力系数基本重合，说明气动翼的影响在62.5 m ＜x＜72.5 m内，因此仅对该区间进行详细分析.气动翼前方车体的表面压力幅值与气动翼角度呈正相关，如图6（b）中左侧放大图 ① 所示，负压占据主导，因此积分面积为负值，但绝对值随气动翼角度增加而减小.气动翼后方车体的表面压力呈现先减小后增大再减小的趋势，波谷是流经气动翼的气流在气动翼后方形成的涡的位置，负压较大.涡后方气流紊乱使得空气流速下降，负压减小，甚至气动翼角度为5°的工况变为正压，即图6（b）放大图 ② 的波峰所示，气动翼后方压力变化规律与图5（b）的结论一致.气动翼后方车体表面压力与Cp= 0所围成的积分面积随气动翼角度的增加而增大，与气动翼前方车体的综合影响使总面积呈现先减小后增大的趋势，在12.5° 位置出现极小值，因此安装 12.5° 气动翼的磁悬浮列车尾车气动升力最小.

图6 气动翼及尾车y = 0截面压力系数分布Fig.6 Pressure coefficient distribution of tail car and aerodynamic wings at plane y = 0

2.2 气动翼数量对列车气动性能的影响

为进一步改善高速磁悬浮列车的尾车升力特性，在确定了升力特性最优的12.5° 气动翼后，以气动翼与车体切线角度保持不变为基准，在第1个气动翼后方添加第2个、第3个气动翼，都位于前方气动翼形成的压力波峰后，也即图6（b）中右侧放大图中的波峰后方，安装了2个、3个12.5° 气动翼的高速磁悬浮尾车分别命名为T2、T3，T3的3个气动翼分别命名为T3W1、T3W2、T3W3，列车及气动翼编号如图7所示.

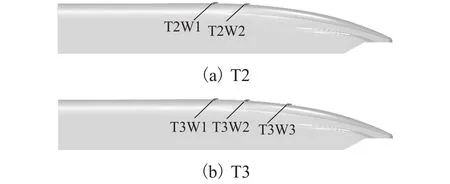
图7 气动翼位置及编号Fig.7 Positions and numbering of aerodynamic wings

对安装多个气动翼的高速磁悬浮列车进行数值模拟计算，气动翼对头车及中间车气动升力及阻力仍基本没有影响，只提取磁悬浮列车尾车及气动翼的气动力系数进行对比，如表2所示.由表2可知：不同位置的气动翼产生的气动阻力基本相同，气动阻力系数都为0.002，气动翼的存在使尾车车体的气动阻力有所降低，但其自身产生的气动阻力大于车体的减少量，车体的气动阻力系数仍随着气动翼数量的增加而增大.与不安装气动翼的原始高速磁浮列车相比，安装了1、2、3个气动翼后整车气动阻力系数分别增大1.0%、1.4%、1.9%.

不同位置的气动翼产生的气动升力存在差异，气动翼的气动升力由第1个气动翼向列车鼻尖方向递减.气动翼的扰流作用使流线型位置的负压区被破坏，如图8所示.图中：安装1个气动翼的高速磁悬浮尾车命名为T1.由图8可知：流场压力升高，车体气动升力减小.随着气动翼数量的增加，气动翼自身的气动升力的增加量与尾车气动升力的减少量达到平衡，T2、T3的气动升力系数都为0.543.

图8 气动翼附近流场压力系数分布Fig.8 Pressure coefficient distribution of flow field near the aerodynamic wings

提取3种磁悬浮列车尾车车体及气动翼在y=0截面的表面压力系数，如图9所示.

由气动翼前方的正压波峰及后方的负压波谷峰值变化规律可以看出：向尾车鼻尖方向气动翼的表面压力绝对值逐渐减小，与表2中气动升力系数变化规律一致.由图9中放大图 ① 得到3种列车W1气动翼的迎风侧压力基本一致，也即后方存在气动翼与否对前方气动翼迎风侧的压力基本没有影响.但气动翼背风侧及其附近列车表面压力受后方气动翼的影响较大，如图9中放大图 ②、放大图 ③所示.若后方存在气动翼，则前方气动翼背风侧及其附近的列车表面压力较小，是因为后方气动翼对气流的阻碍作用使空气流速降低，进而减小了负压幅值，说明后方气动翼对前方气动翼背风侧及其附近车体压力影响较大.

表2 尾车及气动翼的气动力系数Tab.2 Aerodynamic force coefficients of the tail car and aerodynamic wings

图9 气动翼及尾车y = 0截面压力系数分布Fig.9 Pressure coefficient distribution of tail car and aerodynamic wings at plane y = 0

综合上述分析：T2、T3磁悬浮列车与安装单个气动翼的磁悬浮列车相比，尾车气动升力有进一步的减小，T2与T3磁悬浮列车具有相同的气动升力，但T2气动阻力较小，因此，T2磁悬浮列车气动性能相对更优；T2磁悬浮列车与原始磁悬浮列车相比尾车气动升力减小4.6%，整车阻力仅增加了1.4%.

3 结 论

通过对开展过风洞试验的高速磁悬浮列车进行数值模拟计算，并安装气动翼改善尾车气动升力，研究了气动翼角度、数量对尾车气动特性的影响，主要得到以下结论：

1） 在高速磁悬浮尾车安装气动翼对头车、中间车的气动力及周围流场基本没有影响，5种角度的气动翼磁悬浮列车头车、中间车的气动阻力、气动升力系数都与原始磁悬浮列车基本相同.

2） 气动翼自身气动阻力随角度的增加而增大，从而尾车及整车气动阻力也增大；气动翼自身气动升力随角度的增加而减小，尾车气动升力则呈现先减小后增大的变化趋势，在气动翼角度为12.5° 时最小，与原始磁悬浮列车相比气动升力系数减小3.9%.

3） 在尾车安装多个气动翼时，不同位置气动翼的气动阻力系数相同，但尾车的气动阻力系数随气动翼数量增加逐渐增大；不同位置气动翼的气动升力存在差异，并向鼻尖方向递减.安装2、3个气动翼的磁悬浮列车T2、T3与安装单个气动翼的磁悬浮列车相比，尾车气动升力有进一步的减小，T2与T3磁悬浮列车具有相同的气动升力，但T2气动阻力较小，因此，T2磁悬浮列车气动性能相对更优.T2磁悬浮列车与原始磁悬浮列车相比尾车气动升力减小4.6%，整车阻力仅增加了1.4%.

本研究仍存在一些不足之处，在安装气动翼改善高速磁悬浮列车尾车气动升力时未能同时兼顾减阻，虽减小了尾车气动升力但也增大了其气动阻力，后续将继续开展相关研究，尝试设计出能够同时减小尾车气动升力与气动阻力的气动翼.

致谢：中央高校基本科研业务费 （2682021ZTPY 124）.