数学资优教育视域下的“学材再建构”案例研究
——以勾股定理及其应用为例
2022-06-17重庆市第八中学校400030
重庆市第八中学校(400030) 程 灿
重庆八中宏帆中学校(400021) 宋俐莹
1 问题提出
何为资优教育,李翠翠(2019)指出资优教育亦称为天才教育、英才教育、超常教育,是现代学校教育的一种理念,其逻辑起点是维护教育公平,并充分发挥资优生的优异才能,为社会输送创新型人才[1].资优教育一直关注人才的资质及其对应的培养方式,为创新人才的培养提供了重要保障.何为数学资优生,刘永东(2017)认为数学资优生是指在数学学习上具有思路清晰、敏捷的思维能力,同时具备较好的概况能力和创造能力的学生[2].数学资优教育在创新型人才的培养与选拔中发挥着不可替代的作用.目前国内培养数学资优生的主要途径有各类竞赛培训活动、理科实验班、课程改革融合班等.由于我国数学资优教育的研究起步较晚,系统制定和精心修订的课程、教材还比较缺乏,初中数学资优教育还在摸索中前行.
2017年,国家级教学成果奖一等奖获得者李庾南及团队在“自学·议论·引导”教学法原有理论和实践的基础上,提出“学材再建构、学法三结合、学程重生成”的“三学”操作规则.李庾南认为对“学材”再建构,是指根据教学目标和学情对原教材的内容进行增减,对教材中知识呈现的顺序和详略,知识呈现的背景、方式、方法及学习的策略等进行调整或重组[3].针对数学资优生的培养,我们的步子也许还可以更大,只要基于学生的认知基础,顺应学生最近发展区,有利于学生数学思想方法和数学分析、解决问题能力培养的重构学材都可以纳入资优教育教学实际中.
笔者结合初中课改融合班任教经历,在数学资优教育视域下尝试对北师大版《义务教育课程标准实验教科书·数学》(以下简称“教材”)中勾股定理及应用相关内容进行整合,并做分析、研究.
2 案例呈现与研究
2.1 教材内容安排
教材中勾股定理相关内容安排见表1,内容编排遵循整套教材的知识螺旋式展开、递进之体例.八年级上册第1 节第1 课时主要是在网格中探索、验证勾股定理,并简单应用勾股定理.教材先作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向三角形外作正方形,分别利用直接数小正方形个数或割补拼凑来表示每个正方形的面积,由此得出直角三角形边长平方关系.第1 节第2课时去掉网格,利用“赵爽弦图”等验证勾股定理.同时在“议一议”环节中,给出网格背景下的斜三角形(钝角三角形或锐角三角形),让学生判断其三边是否还满足a2+b2=c2.第2 节主要通过给几组三角形的边长,让学生判断这些三角形是否为直角三角形,并与同伴交流,教材正文未给出勾股定理逆定理的证明.第3 节主要内容为勾股定理应用,主要解决立体图形侧面最短路径问题.下册第2 节正文部分严格论证了勾股定理逆定理,并在“读一读”材料中给出了欧几里得在《几何原本》中证明勾股定理的大致过程.
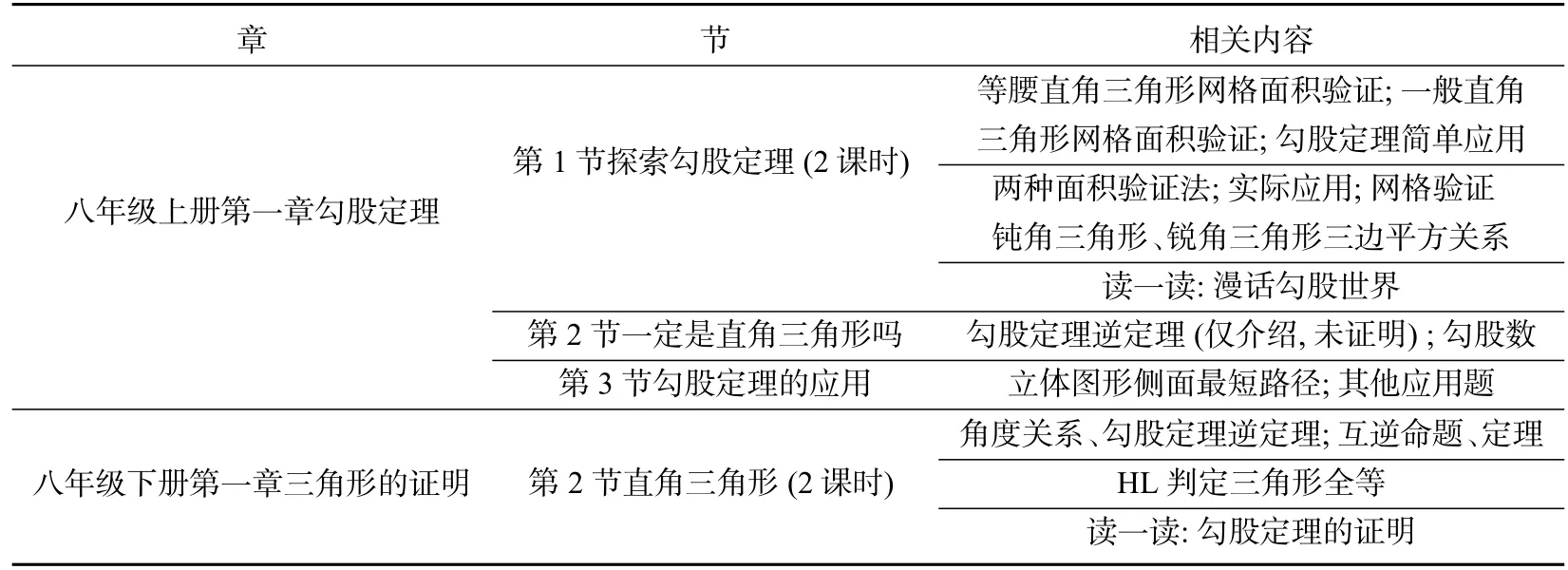
表1 勾股定理相关内容分布
2.2 学材建构思路
熊斌(2018)认为普通教育数学课程(特别是义务教育阶段)反映的是大众数学,较少考虑数学资优生的需要[4].笔者认为针对数学资优生的勾股定理教学可以做一些新的尝试,比如纵向整合上、下两册教材相关内容,理顺内容之间的逻辑顺序,设计结构框图如图1所示.
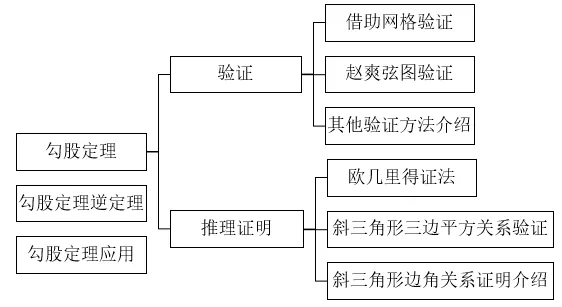
图1
对勾股定理的探究可以始于网格验证,但落脚必须高于此,虽然勾股定理和斜三角形中边角关系的推理证明等已经超出《义务教育数学课程标准(2011年版)》(以下简称《标准》)要求,但对数学资优生而言,如果在课堂上不用跳就摘到“桃”,那这样的“桃”是没有多大魅力和价值的.因此,为了数学资优生的能力最大化发展,在学材建构过程中,除了纵向整合,还可以适度横向拓展、加深.比如可以提出启发学生思考的问题:
(1)给定直角三角形某两边,第三边长度唯一确定吗?
(2)为什么要开门建山地研究线段的平方关系而不是研究线段的线性等量关系?
(3)在网格中对构造的三个正方形面积关系的研究毕竟只是一种直观验证,是否可以通过演绎推理证明勾股定理?
(4)在斜三角形中,三边关系a2+b2=c2还成立吗?
如果能让资优生顺应这些新的尝试,且从这些深度探究问题的解决过程中获得灵感,其分析问题、解决问题的能力必定更上一层.
2.3 学材建构案例分析
案例1执教第1 课时,笔者首先选择在网格中验证勾股定理,并对网格中的验证进行变式,让格点直角三角形三条边都不与网格的水平和竖直线重合,学生从直接数单位小正方形个数求面积,变成了通过割、补来计算三个正方形面积,实现了难度的提升;接着,去掉网格,让学生思考,又该如何验证,因为在网格计算中学生有将正方形“改斜归正”地割、补的探究经验,学生再来理解“赵爽弦图”就会容易得多;最后,赏析八年级上册教材阅读材料“漫话勾股定理”中的其他验证方法.第2 课时,介绍八年级下册教材阅读材料“勾股定理的证明”中的欧几里德证法,如图2,ΔFAB面积为正方形GFAC面积的一半,ΔCAD面积为矩形AMND面积的一半,又因为ΔFAB≌ΔCAD(SAS),故ΔFAB面积等于ΔCAD面积,所以正方形GFAC面积等于矩形AMND面积.同理,正方形HCBI面积等于矩形MNEB面积,故AC2+BC2=AB2.这一证明十分优美,极大地开拓了学生眼界.另外,在网格背景下通过计算可判断钝角三角形两短边的平方和小于最长边的平方,锐角三角形两短边的平方和大于最长边的平方.提出两个思考问题:
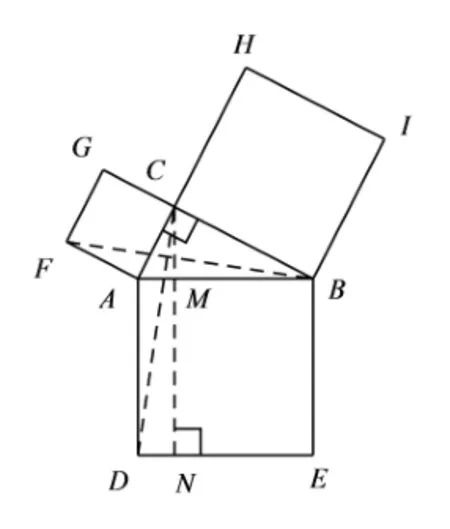
图2
问题1去掉网格背景,任意斜三角形三边平方的不等关系还成立吗?
问题2不等关系能否转化为等量关系,即钝角三角形两短边的平方和比最长边的平方小多少,锐角三角形两短边的平方和比最长边的平方大多少?
解答1如图3,钝角ΔABC中,∠ACB >90°,按照前面的证明思路,有AC2=S正方形GF AC=S矩形PFAQ−S矩形P GCQ=S矩形ADNM−S矩形P GCQ,故AC2
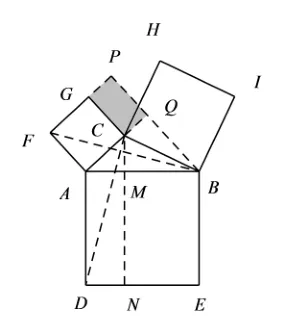
图3
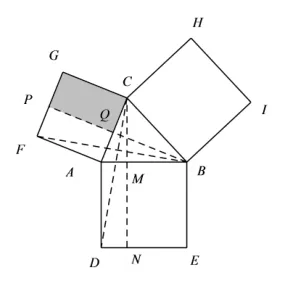
图4
解答2如图4,S矩形P GCQ=CG·CQ=AC·BC·cos ∠ACB,故AC2=S矩形ADNM+AC·BC·cos ∠ACB,同 理,BC2=S矩形MNEB+BC·AC·cos ∠ACB,故AC2+BC2=AB2+2AC·BC·cos ∠ACB.思考问题2 竟与余弦定理产生了关联,同时钝角三角形中的等量关系与钝角的余弦定义以及诱导公式等知识有关,这些知识已超出《标准》要求,因此课堂上仅提出思考,可供资优生课后自主探究.
案例2在处理勾股定理应用一节时,笔者发现教材中的引例可以横向拓展.
例有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm.在圆柱下底面的点A有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画出几条线路,你觉得哪条线路最短呢?
(2)将圆柱侧面展开成一个长方形,从点A到点B的最短路线是什么? 你画对了吗?
(3)蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少?
解析经分析,蚂蚁沿圆柱侧面爬行的最短路程是圆柱侧面展开图中线段AB的长,AB=
以上三个问题难度不大,但考虑到蚂蚁沿圆柱表面爬行时,只从侧面走未必是最近的.随后笔者在课堂上提出“如果圆柱不是开口的,而是加盖的,蚂蚁怎样爬行路程最短”.起初,这一问题并还没有引起学生的重视,大多数学生认为不会影响答案,只有少部分学生开始动笔演算,越算越觉得问题并没有那么简单,慢慢的课堂静了下来,学生头脑动起来了.
在充分思考后,有学生提出可以引入字母来表示数量,如设圆柱体高为h,底面圆直径为d,则要比较h+d与的大小,需分类讨论:当·d时,有故先沿着母线,再沿着上底直径爬行,路程更短;当h >·d时,沿着圆柱侧面展开图中连线AB爬行,路程更短;否则,两种方式路程相同.还有同学提出是否有更短的路程,蚂蚁会不会从侧面爬行至上底面圆上某点,再从这一点向B点爬行.事实上,这一追问颇有难度,已经超出了课堂预设,囿于课堂时间,将这一问题留作课后思考,笔者课后及时将问题整理如下.
如图5,蚂蚁先沿着侧面爬行至上底面⊙O上一点D,再沿着线段DB爬行至点B,爬行路程除了与圆柱体高h与底面圆直径为d有关外,还与∠COD有关,设∠COD=θrad,则爬行路程为曲线AD与线段DB的长度之和,表示为利用求导,得出当时,l(θ)最短.
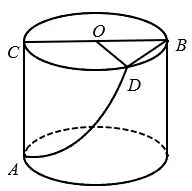
图5
3 结语
以上案例是笔者根据资优生勾股定理及其应用的教学需要,基于教材展开的内容更丰富、逻辑更自然的教学设计.以教材内容为核心,进行恰当的纵向整合,不断深化对勾股定理的认知,切实巩固“四基”;调整教材内容顺序,将阅读材料、学生课堂生成的问题等内容也纳入到课堂教学中,将学材横向拓展,让学生在多种活动和学材中体验知识生长,很大程度上提升了课堂教学的容量;欧几里得证法变形后为斜三角形的研究理顺了研究思路.同时,将立体图形侧面最短路径进一步拓展,变单一结论为分类讨论,无不体现从相同的模型范式中寻求更高能力的思维生成.
初中数学资优教育需要教师根据教学实际情况,从教材内容、学生提问等方面提取有效、高质的“学材”,需要纵横延伸,需要教师具备“学材再建构”能力,以追求学生的最大发展.
