融合交叉学科知识,彰显数学应用价值*——以“圆锥曲线的光学性质及其应用”数学实验课为例

上海市七宝中学(201101) 童永健

1 拓展课堂,应用数学

传统的高中数学教学内容多与现实生活较远,需教师在日常教学及课堂设计中刻意挖掘,从而让学生体会所学知识在现实中的应用价值.我国《普通高中数学课程标准》提出的数学学科核心素养中包括“数学抽象”和“数学建模”即与学生应用数学,联系实际有很大的关联,特别是“数学建模素养”,课程标准指出:“数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养”,同时,对高中学段数学建模活动的开展有着明确的要求[2].

另一方面,交叉学科的知识在高中数学教学中呈现得并不多,更多还是各自学科各自为战,这也可以认为是高中数学与现实生活割裂的原因之一.而数学不仅与物理、化学等理工类学科有着密切的联系,也在社会科学中扮演着重要的角色[3],若能充分挖掘,精心设计,不仅能够激发学生学习兴趣,对概念、知识的本质也能有更立体的诠释.

数学实验是高中学段较新的概念,实验以学生为主体,通过动手操作,借助数学知识和方法,参与到探究活动中,并探求规律或答案.有别于传统知识习得和高考评价体系下传统数学课程实施的方法,数学实验更多要求学生亲自参与与实践,是“双新”背景下育人方式改革的一条尝试路径.

以数学核心素养的培养为目标取向,以交叉学科知识的融合为依托的数学实验教学内容设计,能够彰显数学的现实应用价值,让学生“更易学”、“更愿学”.笔者认为,以数学实验课的形式为载体,以传统数学课程中的拓展知识为切入点,融合交叉学科知识,以及简单的模型思想,是培养学生数学建模素养,在高中拉近数学本体知识和现实应用距离的有效途径.以下就以一节数学实验课为例,说明运用交叉学科内容在课堂中的融合,以体现数学在现实中的应用.

2 探究发现,融合数理

2.1 趣味实验,引发思考

从高空抛出垂直落体的小球,经由反射面反弹汇聚到一点的实验视频.

师:哪个反射面可使球反弹后汇聚到一点? A:圆弧;B:半椭圆;C:抛物线

生:抛物线,如果把自由落体的小球看成平行光线,这个实验体现了抛物线一种聚光的性质.

问题一你能用准确的数学语言概括抛物线的这种聚光性吗?

生:抛物线的光学性质:在抛物线开口侧,一束平行于对称轴的光线射向抛物线,经过抛物线反射会汇聚到焦点,反之,从抛物线焦点发出的光线,经抛物线反射,反射光线平行于对称轴.

设计意图通过一个大型的实验,引起学生兴趣,引发学生思考,同时引出对圆锥曲线光学性质的探究[4].

2.2 深入探究,总结规律

2.2.1 探究活动:直线的包络线与抛物线的光学性质

问题二为什么从抛物线焦点发出的光线,经过抛物线反射,反射光线会平行于对称轴?

数学实验:折纸实验:

步骤①如图,将矩形的纸对折得l0,在l0上取一定点F;

②将纸对折使底边l上若干个点Mi与点F重合;

③画出若干条折痕mi;

④观察这些折痕所围成图形的形状.

师:请思考:(1)观察所围的图形是什么曲线? 生:抛物线.

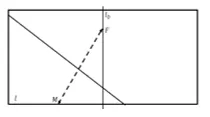
(2)所围曲线和折痕所在直线有什么位置关系? 生:直线与曲线相切,是切点.

师:包络线的概念:把与一族直线中任意一条直线都相切的曲线称为这族直线的包络.

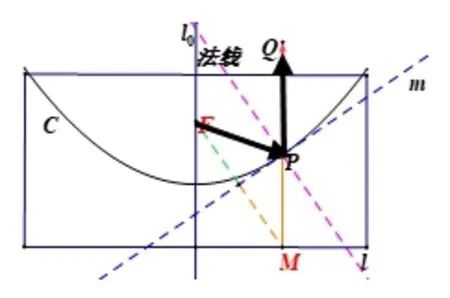
探究为什么经由抛物线反射的反射光线PQ平行于对称轴l0?

将上述问题抽象成数学问题:(3)已知抛物线C的对称轴为l0,准线为直线l,焦点为F,F是抛物线上任意一点,|PF|=|PM|,m是过点P的切线,光线FP从F点出发,在P点处反射,反射光线为PQ,求证:PQ//l0.

生: 利用光的反射原理,通过角的等量代换,可证Q,P,M三点共线,由抛物线的定义,MP即为P到准线l的距离,即MQ//l0.

师:抛物线光学性质的本质:由焦点出发的光线,经过切线反射,反射光线与对称轴平行.

设计意图通过学生探究活动,以及教师层进式的引导,借助于包络线的概念及其与切线的关系,帮助学生一步一步揭开抛物线光学性质的本质,体现相关内容的探究性、创新性及问题解决的渗透.

2.2.2 圆锥曲线的光学性质

师:课后实践:自己动手,借助于折纸实验,探究椭圆和双曲线的形成:

观看几何画板课件演示.

师:问题三:你能根据这一过程概括椭圆与双曲线的光学性质吗?

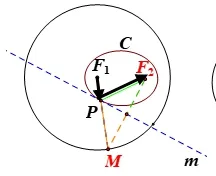
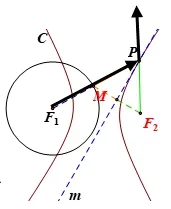
生:椭圆的光学性质与双曲线的光学性质

设计意图归纳总结圆锥曲线的光学性质,让学生类比抛物线的问题研究方法,进行验证,进一步加深对圆锥曲线光学性质的理解.

2.3 发散推广,深度应用

2.3.1 圆锥曲线光学性质在现实中的应用举例

椭圆回音壁;音乐厅;医用体外碎石机;电影放映机

双曲线路口反光镜;汽车后视镜;柔光箱;喇叭

抛物线太阳炉;手电筒;探照灯;远光灯;雷达;射电望远镜.

总结圆锥曲线光学性质在现实应用中的特点:

生:椭圆:汇聚、增强;双曲线:可发散可汇聚,发散时让光减弱,照射面更广;抛物线:可发散可汇聚,发散时平行光线照射距离远.

设计意图结合数学与物理和现实,体现圆锥曲线光学性质的应用价值,让学生体会数学知识在现实中的运用.

“中国天眼”的故事:中国天眼及其总工程师南仁东.

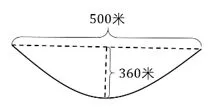
例1“中国天眼”的原理与卫星锅类似,锅面是一个巨大的抛物面,信号经抛物面反射,被接收器接收,假设抛物面截面口径是500 米,“锅口”与底部高度差为360 米,试建立合适的直角坐标系,计算:当接收器安置在距“锅底”多少米处时,信号接收效果最佳?

设计意图介绍了“中国天眼”这个伟大的工程和南仁东先生的事迹,融德育于数学,通过介绍,学生能够了解射电望远镜的基本原理,提升爱国情怀.在解题中,学生需自己建系解题,体现简单的建模过程.

2.3.2 圆锥曲线光学性质在数学解题中的应用[5]

(1)角平分线有关问题

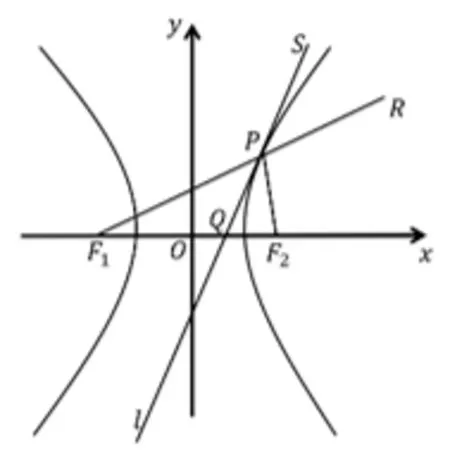
例2P为双曲线C:上任意一点,F1,F2分别为其两焦点,过P作双曲线的切线l,与x轴交于点Q,连接F1P并延长至R,试在图中找出一组由双曲线反射的光线,并求证:PQ平分∠F1PF2.

(2)利用光学性质求轨迹

例3已知P是椭圆C:上的一个动点,连接F2P并延长至F′1,使|PF′1|=|PF1|,连接F1F′1,过点P作椭圆的切线l,l与F1F′1交于点Q,则Q点的轨迹方程是____.(x2+y2=16).

变式双曲线相关问题

设计意图从“形”的角度出发,利用切线反射光线的本质,帮助解决数学问题,加深学生对圆锥曲线光学性质本质的理解.

2.4 归纳提升,数理融合

师:本节课的学习内容,数学思想方法.

总结强调数理融合,强调数学应用.

3 分析课例,深化主题

3.1 课例分析

本节课的教学目标包括让学生了解并能够运用圆锥曲线的光学性质;探究其原理,体会数学与物理知识的交叉融合,以及数学在现实中的应用;培养学生主动探索的精神,提升数学抽象和数学建模的核心素养.

体现数学与现实联系的应用应是本节课的重点和难点,而探究的过程和圆锥曲线光学性质的理解则是学生把握问题的突破口.

本节课结合沪教版教材中的相关内容,将教材中椭圆的光学性质推广到三种圆锥曲线,并探讨了其原理,拓展了教材内容的外延,同时紧扣圆锥曲线的定义分析、解决问题,深化学生对圆锥曲线的理解,挖掘了教材的内涵.

课例从引入到探究再到与现实的联系均有一定的创新,以数学实验为主线,形式较为多样,数学实验活动的过程给予学生较多的“台阶”,引导学生顺利抽象出,并解决数学问题.例题的选择包含了简单的建模过程,将现实情境设计成数学问题,将数学与德育相融合,后两例利用概念的本质指导解题,难度递进,也与前半部分的探究相呼应,体现探究的价值.例题的选用,拓宽了学生的思路,教学的主题,能够将问题化繁为简,数形结合的思想方法,提示学生解题前用心思考、细致品味、三思而行.

3.2 核心素养指导下的拓展课教学设计思路

依托本节课的教学设计,笔者对核心素养概念下的传统数学课堂进行了一番思考.首先,可以拓展内容及拓展课为切入点,逐步深化核心素养的体现,因为拓展内容相对常规知识结构下的内容设置有较大的“改动”和发挥空间,而其往往能够起到打开学生思路、拓宽学生视野、提升学生兴趣的作用.是体现数学建模素养,和培养问题解决能力的“沃土”.

其次,如何将数学和现实有机融合是时下高中数学教学中热议的话题之一,其过程体现了数学建模素养培养的渗透.而学生迫于考试的压力和内容设置的问题,在学习中往往是将数学与现实割裂的,这从某种程度上让数学学习变得更为抽象和困难.在相关的活动设计和改进中,应更多利用现实中真实存在的例子和素材,如本课例中的引入,及所举圆锥曲线光学性质应用的例子,将实验和其他学科知识融合进来,不失为一个有效的思路.

再者,交叉学科知识在传统高中数学课堂中的渗透是一个较新的话题,利用其他学科的知识来帮助将数学问题具体化,也体现了数学抽象的素养.提升了学生综合问题解决能力的作用.

最后,高中数学的抽象性对青少年而言是一个不小的挑战,数学实验概念的引入,为学生提供了“做中学”的方案,如本课例中的“折纸实验”.通过观察、动手、尝试,化抽象为直观,“实验”实则是一个小型的研究过程,能够更好地帮助理解,加深记忆.