提升学生学会数学思考的基本策略

广东省东莞市虎门中学(523900) 司徒超旋

广东省东莞市东莞中学(523005) 赵银仓

有位数学家曾经说过,学生们在中学阶段所接受的数学知识,进入社会后,没有机会直接应用,唯有数学精神、思维方法和策略等,使他们终生受益.可见数学思维会影响学生发展的终身,要发展学生的数学思维,就要让学生学会思考,只要学会思考,并能深度思考,才能发展数学核心素养.

1 让学生学会思考,才能促进素养的落实

数学素养的内涵和要求是多方面,在教育教学的过程中让学生学会思考,就是能理解数学问题,广泛联系相关数学知识,进行深度的探究问题解决的路径,无疑是非常重要的一个方面.学生思考问题解决的过程中,体验对数学问题的抽象分析过程,发展抽象素养,在找到问题中量之间的关系,使问题转化易于解决问题的过程中,锻炼了学生的数学建模与逻辑推理能力,提升数学建模与逻辑推理素养,数学推理离不开数学运算,数学抽象离不开数学想象,这必然发展了数学运算与直观想象素养,因此让学生学会思考,并能深度思考,一定能极大地提升学生的数学思维的品质,进而提升学生数学核心素养,促进学生全面发展,终身受益.

2 遵循数学思维策略,促使学生学会思考

数学思维能力的提升,要遵循数学思维的原则、规律,使思维过程少走弯路.本文拟就探讨数学思维应遵循的基本策略,并举例说明其应用.

2.1 简单化策略

在数学中,往往未知与已知,高次与低次,空间与平面等问题互相联系,互相转化.从解决问题的思维过程来看,通常是化繁为简.主要途径是:(1)分解为简单问题的组合.从已有的认知结构出发,设法将较繁的问题分解为按一定方式相联系的简单问题,分步解决;(2)分解为若干同类的子问题.根据某一本质属性的差异,分为不同的种类,分类解决;(3)抽象为基本问题的推广.对于抽象复杂问题,从同类特殊情形中寻找可推广的结论和方法,迂回解决原问题.这里将繁转化为某个简单问题,或几个简单问题的组合.找到这(些)“简”的问题,将它解决,原有“繁”的问题也迎刃而解.

简单化策略是指这种化陌生为熟悉,高级为低级,复杂为简单的思想方法.这种对问题简单化的过程中蕴含着要理清问题中各种量及其关系,概念之间的联系,问题之间逻辑关系,有助于发展学生的数学抽象素养和推理素养.

例1 设复数z=3 cosθ+i2 sinθ,并设复数z的辅角为α,求函数y=tan(θ−α),(0<θ <)的最大值以及对应的θ值.

分析 此问题可分解为:

(1)求α的正切值.由0<θ <知tanθ >0,且

(2)将tan(θ−α) 表为θ的函数.y=tan(θ−α)=

(3)求最大值及相应θ.

这种分解与组合,使得复杂问题简单化,思维自然流畅,逻辑关系清晰,条理性强.对于数学基础较弱的学生,可以帮助学生找到解题的思路,成功的体验,能唤醒学生学习数学的兴趣与信心,发展学生的运算、推理与逻辑素养.

2.2 等价变换策略

如果命题A 成立当且仅当命题B 成立,那么就称A 和B 为等价命题.记为A⇔B.能使变换前、变换后的命题等价的变换叫做等价变换.等价变换的主要途径有:

(1)数学语言间的互译.灵活地进行语言形态的变换,发挥它们各自的优势,发散思维,开阔思路;不同形态的数学语言(文字语言、符号语言、图形语言)的互译,往往能全方位,多角度地审视题目,简缩思维过程,摆脱思维受阻的困境,有利于培养思维的广阔性.

(2)引入轴助(变)量.引入新的(变)量,促使原问题的形式结构向易于理解和解决的方向转化;

(3)恒等变形.通过与已知问题结构的对比,找出异同,变异为同;

(4)数形转换.将几何的直观和代数的灵活相结合,灵活地进行数形的转化,不断优化解题的思维过程;

(5)图形变换.利用某种变换手段恰当地进行图形变换,创造新的问题情境,寻求简明快捷的解题途径.

等价变换的过程就是不断地联想类比与变形推理的过程,能够丰富学生的想象力,增强推理能力,发展学生的想象与推理素养.

例2设a1,a2,…an都是正数,证明不等式:

分析1

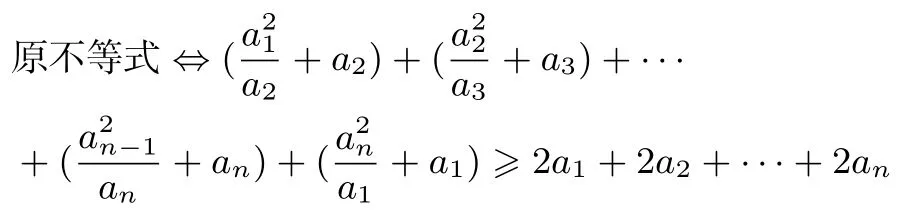
分析2

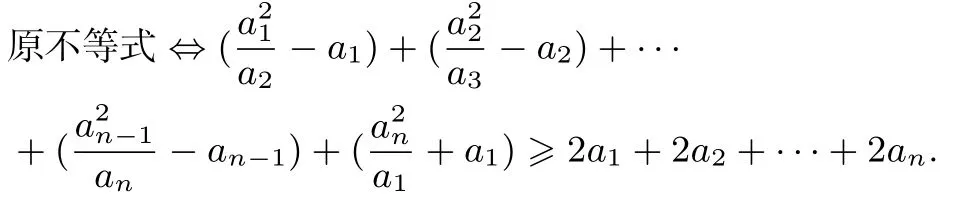
由a >0,b >0 时,−b >a−b成立,知原不等式成立.

分析3

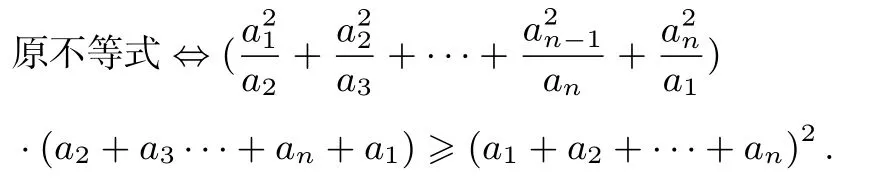
由柯西不等式知成立.

对于某些问题,从其形式结构出发,与原有的认知结构联想类比,找出之间异同,利用它们结构的相似性,进行恒等变形,应用已有结论导出新的结论.这种思维的策略有助于培养思维的想象力,灵活性与深刻性,引导学生寻找疑难问题的数学本源,能促进学生的推理素养的提升.

2.3 映射反演策略

如果两个命题或系统的内容、形式、结构之间存在某种相似性,那么设法在它们之间建立一种对应关系,把原问题映射到其它领域中去解决,然后反演回原来的领域中得出问题的解答.这种解决数学问题的方法叫映射反演原则.这里“映射”指实现命题转换的某种对应方法或变换手段,而“反演”是将变换后求得的解答再转换成原来问题的解答.

实施映射反演,就是一种构造的方法,通过类比联想,利用映射构造新的问题,使原来困难的问题转化为易于解决的问题,问题解决的思维过程中包含着联想、构造、抽象与推理等思维要素,能发展学生的想象、抽象、推理与运算素养.

例3求sin220°+cos280°+的值.

分析对于每个给定的x ∈R,sinx,cosx之间建立对立关系,产生对偶式可帮助解题.于是设则相加得

例4集合S={1,2,···,18}的五元子集S1={a1,a2,a3,a4,a5}中,任何两元素之差不为1,这样的子集S1有多少个?

分析1若分类考虑,明显太烦.由于S1中的每个元素都在S中且任何两个之差不为1,作子集S′={a1,a2−1,a3−2,a4−3,a5−4},则S′与S一一对应,而S′是1,2,3,···14 的五元子集,故共有个.

分析2原问题可转化为18 名学生中有5 名女生,要排成一排,其中任何两个女生不得相邻,问共有多少种不同的排法?

在解题过程中,采用辅助手段如对偶、换元、排序、赋值、分割、投影、放缩等,寻求与问题相关的对应元素、情境和问题,进行迁移和移植,使难题巧解,这种方法能够培养学生思维的发散性、深刻性和灵活性.促进数学运算、抽象与推理素养的形成.

2.4 猜想验证策略

猜想验证原则是指对某个数学问题通过实验与观察分析,提出该问题具有某种可能结果的猜想,然后多次验证,以逐步认识并找出该问题的解决方法.猜想指对某个新命题结论的猜想,也指对解题方向的猜想.当结论是关于自然数的命题时,通常用数学归纳法证明.

这是一种由特殊到一般的思维方法,学生在长期的学习中形成一般到特殊的思维定势,也就是习惯于演绎推理,不熟悉使用合理推理解决问题的路径,培养学生用猜想验证解决问题能使的思维更加全面灵活,使推理素养进一步落实.

例5求和

分析对于该题,求和既无现成公式可用,也不知往何处化.但联想:S1=时使用错位相消法,可猜想:若能找能这样的α与β,问题便迎刃而解.

不难求验证α=2m+1,β=2m−1 满足要求.于是可求得

猜想验证是探求问题结论的有效方法,它有利于培养思维的灵活性、缜密性、创造性,能综合提高数学素质.

2.5 辩证转化策略

数学中充满着矛盾,如已知和未知,常量和变量,相等和不等,有限和无限,运动和静止,合并与分解等.矛盾着的双方既对立又统一,在一定的条件下,互相转化,互相制约.当直接解决某数学问题有困难时,可转向来探索与该问题相联系的另一相对的数学问题,再利用两者之间的依赖关系求得原问题的解.称这种运用辩证思维策略来探索数学问题的方法为辩证转化原则.

辩证转化这一思维方式能使学生学会从正反两个方面考虑问题,能够培养学生思维的灵活性与深刻性,提升数学的抽象、运算与推理素养.

例6已知数列{an},{bn}满足且a1=b1=1,λ为常数,设cn=an+bn,n=1,2,3,···,求证时,{cn}不可能是等差数列.

分析用反证法.设{cn}是等差数列,于是cn+1=an+1+bn+1=an+bn+(λ−)bn=cn+(λ−)bn,即公差d=(λ−)bn为常数,∴λ=或bn=b1=1.因为λ ̸=,故bn=1.则由bn+1=+λbn得=1−λ得an=1−λ也为常数,再由及an=an+1=常数,导出故λ=与已知λ ̸=矛盾.故得证.

顺向推有困难时就逆推,直接证有困难时就间接证.这种正难则反的辩证思维策略往往使解题易于入手,有利于培养思维的灵活性.

例7求椭圆的内接三角形面积的最大值.

分析由面积射影定理联想到椭圆为一圆柱的截面,升维构造底面半径为轴长为2b,椭圆内接ΔABC在圆柱底面上的射影为圆接ΔA1B1C1,且当ΔA1B1C1为正三角形时,椭圆内接ΔABC的面积最大,易知截面与底面夹角的余弦值为从而求得椭圆内接三角形面积最大值为

在平面上解决该问题,会陷入僵局,无计可施,利用“升”维变换在空间上,茅塞顿开,浅显易见.从问题的结构特点出发,灵活使用“次数”、“维数”的升降的辩证关系,改变思维角度,另辟蹊径.辩证思维的形式是多样的,在数学教学中,灵活应用这些辩证思维的策略,可优化学生的思维品质,提高思维的深刻性与全面性,促进数学抽象与推理素养的发展.

3 结语

通过对所教学校的高中学生数学学习情况的调研和访谈发现,现在高中在数学学习中形成一定的学习习惯和学习方法的定势,让学生养成良好的思考习惯,形成一定的思考能力,有助于学生灵活运用数学思维策略去分析问题和解决问题.只有学会思考,并能深度思考,才能发展学生思维能力,遇到问题才能独立思考并寻找解决的方法,改变过去靠记忆和模仿学习数学的习惯,学会了思考,学生对感受到数学的内在美,会感染和熏陶学生在心底由衷的喜欢数学,钻研数学,才能使发展数学素养得以落实.