以问题为驱动 促进思维发展

广东省东莞市麻涌镇古梅第一中学(523133) 黄若明

1 问题的提出

良好的思维能够帮助学生加深对于数学知识的理解和记忆,让学生更好的理解掌握知识的基本表现形式和推理方法.培养思维品质,是新课程理念下初中数学教学的重要目标.那么,究竟该如何培养呢?

2 思维能力的培养

在实际的初中数学教学中,教师应该精心设计有效问题,通过问题引导的方式,让学生学会思考,并且通过对数学知识的学习,逐渐增强自身解决问题的能力.接下来本人从数学问题设计的角度谈谈自己肤浅的看法和做法.

3 问题设计思路

3.1 变式设计问题,培养学生的多层次思维能力

变式常见有两种: 一题多解——解法多变;一题多变——条件改变或结论改变.抓住问题的本质,改变问题情境,遵循学生认知规律,根据发展需要进行问题设计,促使学生的思维向多层次、多方向发展.

3.1.1 一题多解设计问题

一题多解设计问题要求学生可以从问题本身所包含的变化关系中找到解决问题的不同数学模型,对训练学生思维有很好的作用.

例1求证: 直角三角形中,两直角边的平方和等于斜边的平方.

如图3.1.1,RtΔABC中,∠C=90°,BC=a,AC=b,AB=c.

求证：a2+b2=c2.

证法一毕达哥拉斯的证法

如图3.1.1(1),大正方形的面积=小正方形的面积+4个全等直角三角形的面积和,其中,大正方形的边长为(a+b),面积为(a+b)2;小正方形的边长为c,面积为c2;直角三角形的直角边分别为a,b,面积为列等式:化简得:a2+b2=c2.

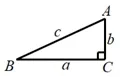
图3.1.1

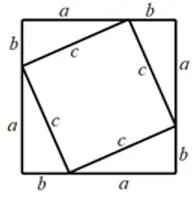
图3.1.1(1)

证法二詹姆斯·加菲尔德的证法

如图3.1.1(2),梯形的面积=等腰直角三角形面积+2 个全等直角三角形的面积,梯形面积为一个直角三角形面积为等腰直角三角形的面积为列等式:化简得:a2+b2=c2.证法三欧几里德证法

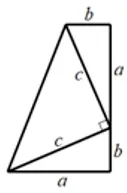
图3.1.1(2)

如图3.1.1(3),分别以直角三角形的三边为边长,作3个正方形,易证: ΔFAB≌ΔCAD.ΔFAB的面积等于的面积等于矩形DLMA的面积的一半,故矩形DLMA的面积为b2.同理可证,矩形LEBM面积为a2.由ABED的面积=DLMA的面积+MLEB面积,得:a2+b2=c2.

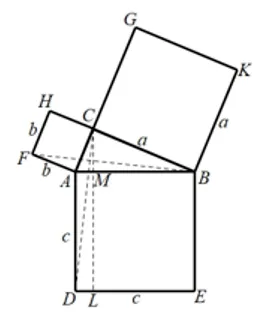
图3.1.1(3)

以上三种证法分别从不同的拼接角度切入,用到了常见图形的面积计算方法,这样一种一题多解设计问题,可以培养学生思维的发散性.

3.1.2 一题多变设计问题

有些数学问题可以改变其个别已知条件,保持问题的实质一致,如能对这些一题多变问题进行归类设计问题,可以使学生思考问题的能力得到提高.

例2如图3.1.2(1),正方形ABCD,E是边BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于点F,求证:AE=EF.

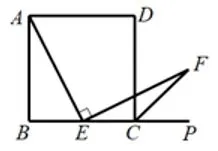
图3.1.2(1)

证明如图3.1.2(2),在AB上取中点G,连结EG,易证ΔAGEΔECF,所以AE=EF.

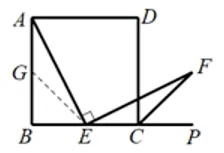
图3.1.2(2)

变式1如图3.1.2(3),若把“点E是边BC的中点”变为“点E是线段BC上的任意一点(端点B、C除外)”,则结论AE=EF还成立吗?

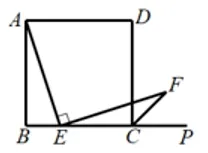
图3.1.2(3)

分析如图3.1.2(4),E在线段BC上,在AB上取点G,使AG=EC,连结GE,证明ΔAGF≌ΔFCF,得AE=EF.

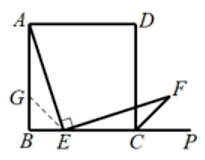
图3.1.2(4)

变式2如图3.1.2(5),若把“点E是边BC的中点”变为“点E是BC延长线上的任意一点”,则结论AE=EF还成立吗?

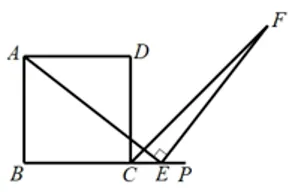
图3.1.2(5)

分析本问题的证明同样可以通过构造全等三角形模型来解决问题.E在BC延长线上,如图3.1.2(6),在BA延长线上取点G,使AG=CE,连结GE,证明ΔAGE≌ΔECF,得AE=EF.

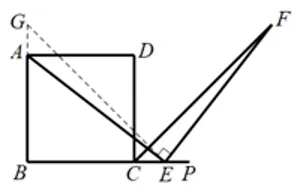
图3.1.2(6)

经过观察、分析、比较,不难发现E 点位置虽然不同,但其本质相同,都属于构造全等三角形模型来解题,只要掌握好这一规律,对于其它同类问题也就迎刃而解了.这样的教学方法,不仅能提高了解题技巧与效率,也培养了学生思维的类比性.

3.1.3 综合变式设计问题

有些问题虽然不同,但实质一样.对于这类问题,要找出问题相同的地方.为此可以有目的地设计问题,培养学习兴趣.

例3如图3.1.3(1),在等边三角形ABC内有一点P,且PA=2,PB=PC=1,求∠BPC的度数.

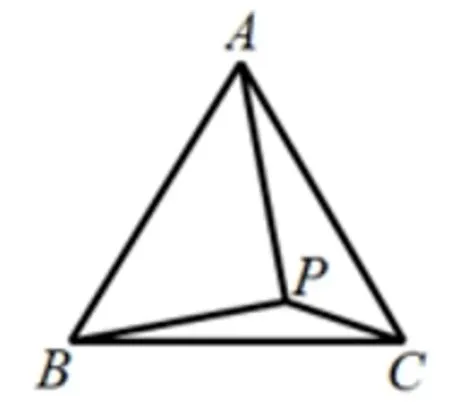
图3.1.3(1)

分析将ΔBPC绕点B顺时针旋转60°,画出旋转后的图形,如图3.1.3(2).连结PP′.可得ΔPP′B是等边三角形,而ΔPP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,问题得到解决.

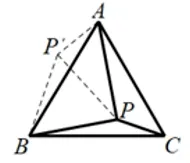
图3.1.3(2)

变式如图3.1.3(3),在正方形ABCD内有一点P,且求∠BPC的度数.

图3.1.3(3)

分析仿照等边三角形的作法,在正方形中将ΔBPC旋转,利用旋转性质和勾股定理逆定理求角度.如图3.1.3(4),将ΔBPC绕点B逆时针旋转90°,得ΔBP′A,则ΔBPCΔBP′A.

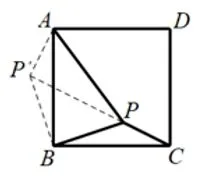
图3.1.3(4)

∴AP′=PC=1,BP=BP′=连结PP′,在RtΔBP′P中,∵BP=BP′=∠PBP′=90°,∴PP′=2,∠BP′P=45°.∵12+22=即AP′2+PP′2=AP2.∴ΔAP′P是直角三角形,即∠AP′P=90°.∴∠AP′B=135°.∴∠BPC=∠AP′B=135°.

3.2 分解设问题,培养思维的有序性

有些问题看似复杂,但通过逐步分解,逐层递进,思路也可以很清晰.

例4如图3.2,国旗上的五角星图案,有∠A、∠B、∠C、∠D、∠E五个角,并且这五个角都相等.

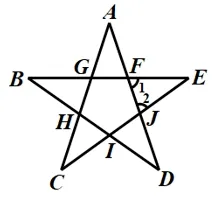
图3.2

(1)∠1 是Δ____的外角;∠2 是Δ____的外角.

(2)∠1=____+____,∠2=____+____.

(3)求∠A+∠B+∠C+∠D+∠E的度数.

分析这道题如果直接求第(3)小题,对大多数学生来说都会有很大的难度,不知从何入手.可是采用分解设问之后,题目难度变小了许多.

3.3 分类讨论题,培养思维的严密性

分类讨论能够将复杂问题简单化,化繁为简,既做到将教学内容条理化又清楚的呈现出问题本质,更易于解决问题.

例5如图3.3,四边形ABCD中,AB//DC,∠B=90°,E为BC上一点,且ΔABE与以C、D、E为顶点的三角形相似.若BC=8,AB=3,DC=4,求BE的长.

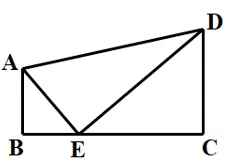
图3.3

分析设BE的长为x,分两种情况:

(1)当ΔABE∽ΔECD时,即:解得:x1=2,x2=6,

(2)当ΔABE∽ΔDCE时,即:解得:

3.4 开放性设计问题,培养思维的创造性

3.4.1 条件开放

此类题目一般采用逆向思维,由结论出发,逆推结论成立的条件.

例6有三个式子: ①a2−ab;②a2−b2;③a2+ab.选择两个式子组成一个分式,并化简.

这个问题只需要考虑结论成立的条件之一就可以了.

3.4.2 结论开放

通常数学证明题都有题设和结论两部分组成,由于结论明确,解题时学生思维受到一定的限制,在教学过程中,我设计了一类只给条件,没给结论的问题.由于没给结论,学生要自己探寻结论,可以培养学生的创造性.

例7在同圆或等圆中,一条弧是另一条弧的两倍,那么它们所对的弦有什么关系?

如图3.4.2 所示,有些学生猜想CD=2AB,有些学生猜想CD <2AB,也有学生AB和CD的大小关系不确定.

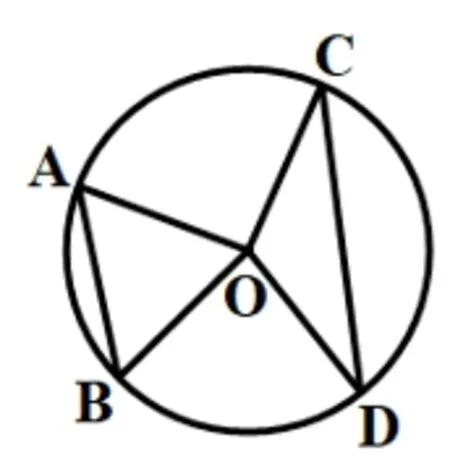
图3.4.2

4 结束语

问题是思维培养的动力和源泉.合理的问题串设置,对于学生思维能力的培养有直接的推动效果.教师发起的问题来源于学生,教师的提问能引导学生更好地解决问题.通过多年的教学实践,笔者深深感到问题选择好一点,学生思维就积极一些.把题海留给老师,把经典留给学生.设计好问题是发展学生思维能力,培养学生良好的思维品质的有效途径.