高中数学变式教学的三性:目标性、时效性、层次性

[摘  要] 针对当前变式教学存在的问题，基于理论研究与教学实践，认为变式教学要有目标性、时效性和层次性，以发展学生的思维.

[关键词] 变式教学;目标性;时效性;层次性

新课改背景下，变式教学已成为一种常态. 每次听公开课，关于变式问题几乎都会涉及. 不难发现，有效利用变式教学，不仅可以扩大教学容量、节约课堂时间，还可以增加课堂情趣，为教学添彩增色.然而，在听课时，笔者发现了一些问题：变式教学存在一定的随意性. 部分教师由于对变式教学的本质理解不透彻，教学中出现了不合常理的现象，如有的不合知识的逻辑顺序;有的不顾学生的认知水平;有的盲目追求面面俱到，使学生陷入了新的“题海”;有的忽视师生互动，只顾自己不停变式，无视学生的情绪，等等. 基于此，高中数学教师在进行变式教学时应注意哪些问题呢？笔者以为，变式教学要有目标性、时效性和层次性.

[⇩] 变式教学要有目标性

对于同一课内容，可以从不同角度设计完全不同的变式问题，但教师需要明确：每一步变式的目的是什么？想让学生做什么？变式的最终目的是什么？学生能有什么收获？因此，在变式之前，教师必须反复斟酌，仔细推敲. 教学要有教学目的，变式教学亦然如此.

案例1 高度问题的计算.

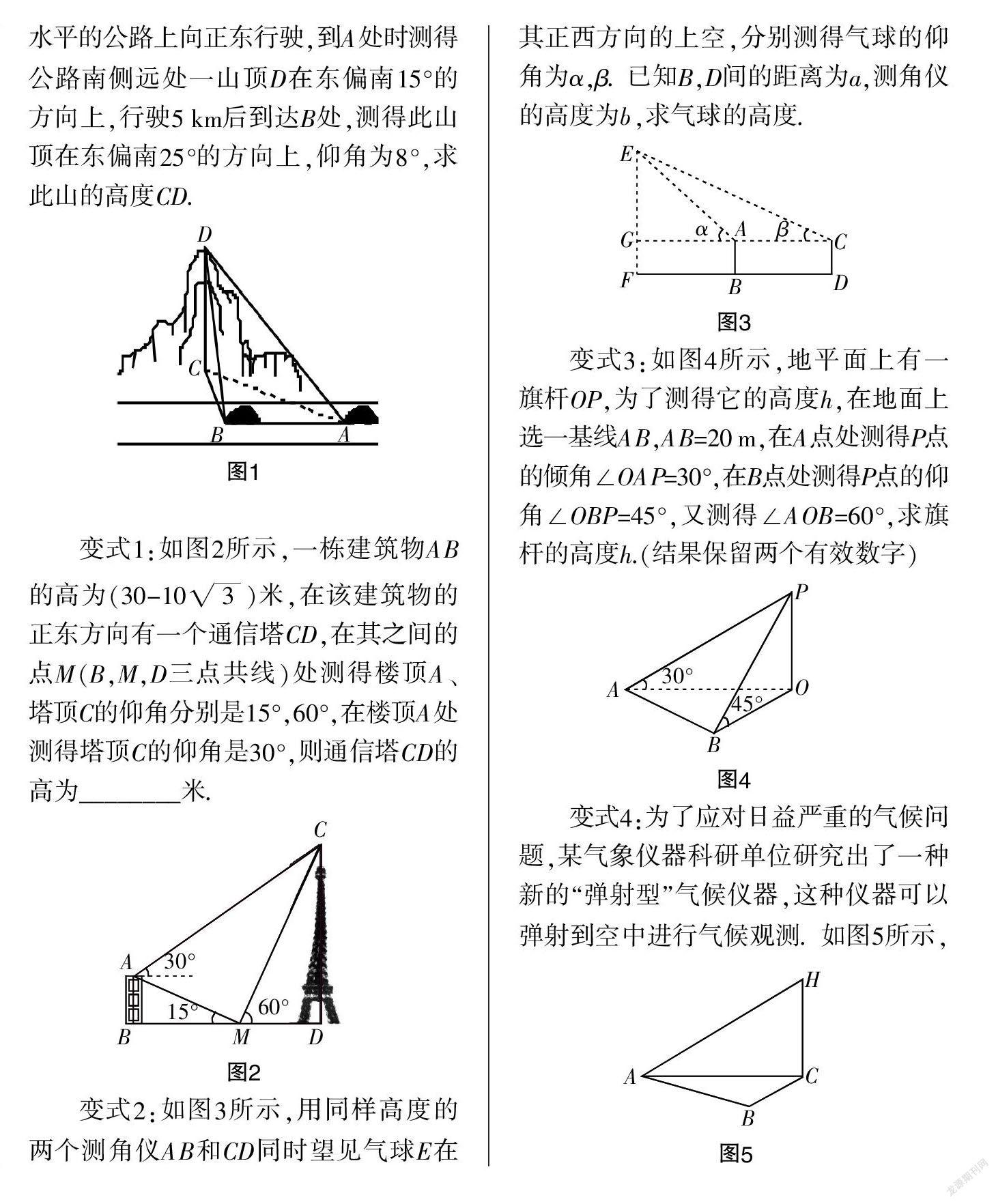
引例：如图1所示，一辆汽车在一条水平的公路上向正东行驶，到A处时测得公路南侧远处一山顶D在东偏南15°的方向上，行驶5 km后到达B处，测得此山顶在东偏南25°的方向上，仰角为8°，求此山的高度CD.

变式1：如图2所示，一栋建筑物AB的高为（30-10）米，在该建筑物的正东方向有一个通信塔CD，在其之间的点M（B，M，D三点共线）处测得楼顶A、塔顶C的仰角分别是15°，60°，在楼顶A处测得塔顶C的仰角是30°，则通信塔CD的高为________米.

变式2：如图3所示，用同样高度的两个测角仪AB和CD同时望见气球E在其正西方向的上空，分别测得气球的仰角为α，β. 已知B，D间的距离为a，测角仪的高度为b，求气球的高度.

变式3：如图4所示，地平面上有一旗杆OP，为了测得它的高度h，在地面上选一基线AB，AB=20 m，在A点处测得P点的倾角∠OAP=30°，在B点处测得P点的仰角∠OBP=45°，又测得∠AOB=60°，求旗杆的高度h.（结果保留两个有效数字）

变式4：为了应对日益严重的气候问题，某气象仪器科研单位研究出了一种新的“弹射型”气候仪器，这种仪器可以弹射到空中进行气候观测.如图5所示，A，B，C三地位于同一水平面上，这种仪器在C地进行弹射实验，观测点A，B两地相距100米，∠BAC=60°，在A地听到弹射声音比B地晚秒（已知声音传播速度为340米/秒），在A地测得该仪器至高H处的仰角为30°，则这种仪器的垂直弹射高度HC=________米.

以上4个变式题目一脉相承，变式1将图形平面化，培养学生的识图能力;变式2将已知条件变成字母，培养学生的三角运算能力;变式3将图形立体化，通过问题的解决培养学生的方程思想;变式4将问题进一步实际化，培养学生分析问题与解决问题的能力. 以上每个变式问题的最终目标一致，都是教会学生解三角形中的一类高度问题.

[⇩] 变式要有时效性

变式教学作为教学的一种必要形式，引入变式无可厚非，但并非想变就变，想什么时候变就什么时候变. 教师应把握好引入变式的时机.只有在恰当的时机引入恰当的变式，教学和训练才能达到预期的理想效果，否则它只是一种形式，有时应用不当反而会起负作用.因此，引入每一个变式，教师都要想什么时候引入最合适，效果最好.

案例2 冪函数的图像与性质的应用.

引例：已知函数f（x）=（m2-m-1）x-5m-3，m为何值时，f（x）：（1）是幂函数？（2）是幂函数，且是（0，+∞）上的增函数？

设计目的：及时巩固学生刚学过的新知.

变式1：幂函数y=f（x）的图像过点（4，2），则幂函数y=f（x）的图像是（  ）

<D：＼DW＼数学教学通讯（下旬）＼2022年＼2022年中等教育下旬3期＼周世彦3-3.tif><D：＼DW＼数学教学通讯（下旬）＼2022年＼2022年中等教育下旬3期＼周世彦3-3.tif>[x][O][y][x][O][y]<D：＼DW＼数学教学通讯（下旬）＼2022年＼2022年中等教育下旬3期＼周世彦3-4.tif><D：＼DW＼数学教学通讯（下旬）＼2022年＼2022年中等教育下旬3期＼周世彦3-4.tif>[A][B][x][O][y][C][D][x][O][y]

设计目的：及时巩固学生对幂函数图像的认识.

变式2：当0<x<1时，f（x）=x1.1，g（x）=x0.9，h（x）=x-2的大小关系是________.

设计目的：及时巩固学生对幂函数在第一象限的图像的认识.

变式3：已知幂函数f（x）=xα的部分对应值如下表（表1），则不等式f（

x

）≤2的解集是（  ）

设计目的：及时培养学生掌握幂函数单调性的应用.

变式4：已知幂函数f（x）=xm2+m-1（m∈N*）经过点（2，2），试确定m的值，并求满足条件f（2-a）>f（a-1）的实数a的取值范围.

设计目的：让学生知道利用幂函数的单调性时切勿忽视幂函数的定义域.

对于幂函数的教学要求并不高，教学大纲的教学安排只有1课时. 因此，这节课的变式不可太多，也不可太难. 对于这类新授课的变式教学，应特别注重时效性，能让学生当堂学习、当堂巩固，进而发挥变式的实效.

[⇩] 变式要有层次性

变式的层次性是指变式时要循序渐进，要有梯度，层次合理，跨度合理.一般而言，从简单入手，拾级而上，变式之间的跨度不宜过大，不能让学生产生畏难情绪，从而畏葸不前. 同样，变式也不可过密，跨度过密往往会出现一些没有价值的问题，不利于学生的思维发展.如何设计有层次性的变式，一切都要从学生的实际出发，设计的问题应尽量接近学生的最近发展区，让各种层次的学生都有所想、有所悟，从而有所收获.

案例3 与焦点三角形有关的椭圆的离心率的求法.

引例：已知F，F是椭圆C的左、右焦点，点P在椭圆C上，且满足PF=2PF，∠PFF=30°，则椭圆C的离心率为____.

变式1：设F，F分别是椭圆C：+=1（a>b>0）的左、右焦点，点P在椭圆C上，若线段PF的中点在y轴上，∠PFF=30°，则椭圆C的离心率为________.

变式2：椭圆Г：+=1（a>b>0）的左、右焦点分别为F，F，焦距为2c.若直线y=（x+c）与椭圆Г的一个交点M满足∠MFF=2∠MFF，则该椭圆的离心率等于________.

变式3：如图6所示，已知点P是以F，F为焦点的椭圆+=1（a>b>0）上一点，若PF⊥PF，tan∠PFF=，则此椭圆的离心率是______.

变式4：已知点P是以F，F为焦点的椭圆+=1（a>b>0）上一点，若∠PFF=α，∠PFF=β，且cosα=，sin（α+β）=，则该椭圆的离心率为________.

变式5：已知椭圆+=1（a>b>0）的左、右焦点分别为F（-c，0），F（c，0），若椭圆上存在点P使=，则该椭圆的离心率的取值范围为_____.

不難发现，以上5个变式题目都是围绕着与焦点三角形有关的椭圆的离心率而展开的，从简单到复杂，从数据的变化到题目结构的变化，从形式相同到本质不同，层层相连，步步为营，环环相扣，让学生的思维不断地螺旋上升，同时也感受到了数学思维的乐趣.

总之，变式教学最终的目的是为了发展学生的思维，因此变式要注意学生的参与度. 教师要时刻做到“眼中有学生，心中有学生，一切为了学生”，否则再好的变式也会毫无意义.