小小A4纸，也有大学问——特级教师唐彩斌《A4纸的数学问题——点线面的平移旋转拓展课》教学片断赏析

文|徐明旭

小学数学领域的拓展课如火如荼地开展着，教师不仅努力在数学课中让学生轻松学到数学知识和技能，还尝试满足他们的个性化需求。最近，笔者有幸聆听特级教师唐彩斌的《A4 纸的数学问题——点线面的平移旋转拓展课》，惊讶于他对单一情境素材的充分挖掘和设计精致课件改变课堂的魅力，令我久久难以忘怀。

片断一：线动成面，学会动态地空间想象。

（课前播放点线面体的视频，感悟点动成线、线动成面、面动成体、平移旋转对称的神奇变化）

师：今天我们来研究一张A4纸，你们知道A4 纸的大小吗？

生：（用直尺测量）A4 纸的大小是21 厘米×29.7 厘米。

师：为了研究方便，我们约定A4 纸的宽20 厘米、长30 厘米。现在我们开始第一个挑战。如果我把A4 纸的宽边沿着长边向右平移30 厘米，空中留下什么图形？

生：长方形。

师：同样以宽边的一端旋转一圈，会形成什么图形？

生：圆形。

师：让你们勇敢地猜一次，长方形大还是圆形大？（学生举手表示猜的结果）请你用精准地计算验证一下到底哪个大。

生：第1 题面积是20×30=600平方厘米，第2 题面积是π×202=1256 平方厘米。（π 取3.14）

师：当我们想的时候还想不出那么大的差别，现在我用一幅图来验证一下。请看，能看出哪个大吗？

生：旋转出来的大。

【赏析：著名的荷兰数学教育家弗赖登塔尔在《作为教育任务的数学》一书中说：“从高层次看，几何是数学的一部分，它是以公理系统的方式组织起来的；但从最低的基本层次上看，几何则是对空间的理解。为了生活得更好，我们就必须了解、探索并征服我们所生存的空间。”在这节数学拓展课中，唐老师利用简单的A4 纸表示数学中的几何图形，以运动的视角打通了计算领域与空间领域的教学目标：一是巩固图形面积和体积的计算公式与方法，二是发展学生的空间观念。课堂伊始，唐老师利用几何画板制作点线面体的微视频，不仅给予学生一场视觉盛宴，让他们直观地欣赏了点线面体之间的对称美与和谐美，还瞬间点燃了他们的好奇心和求知欲，快速进入数学课堂。接着，唐老师用聊天的方式与学生一起认识了这张普通的A4 纸，并由一维的点线拓展到二维的平面，让学生经历观察猜想、计算验证、直观观察等活动过程，引导他们通过计算发现旋转出来的面积比平移的面积要大。这个学习过程不仅帮助学生积累了数学活动经验，还发展了他们的空间观念。】

片断二：面动成体，学会全面地思考问题。

师：如果还是这张A4 纸，沿着与平面垂直的方向平移80 厘米，空中留下的是什么？

生：长方体。

师：还是这张A4 纸，沿着其中一条边旋转，转出来的是什么？

生：圆柱。

师：相信你们的直觉，再猜一次哪个转出来的体积大，哪个转出来的体积小？（学生举手表示猜的结果）赶紧动笔算一算，为了计算方便可以保留π。

生：3 号图形是长方体，体积是30×20×80=48000 立方厘米，4号图形是圆柱，体积是π×20×20×30=37680 立方厘米。

师：你们的计算能力真强。这位同学的结论是3 号图形体积大。但有不同意见，你估计他们会是怎么想的？

生：还有一种情况是以这张A4 纸的宽边旋转，以这张A4 纸的长为底面半径，旋转出来图形的体积是π×30×30×20=56520 立方厘米。

师：我们眼见为实，一个沿着A4 纸的宽边旋转，一个沿着A4纸的长边旋转，你们用眼睛能看得出它们的大小吗？

生：看不出。

师：但是我们计算后很肯定沿着A4 纸宽边旋转的体积更大，现在我们与平移出来的长方体比一比体积，你有什么结论？

生：平移出来的长方体的体积比小的要大，比大的要小。

师：凭空是猜不出来的，所以精准计算才能得出正确结论。

【赏析：《数学课程标准（2011年版）》中指出：一维、二维和三维之间的相互转换，恰是发展学生空间观念的有益举措。根据学生的认知心理和数学学科的特点，数学知识的学习难度是循序渐进的，在本节课的教学设计中也有充分体现。唐老师继续带领学生研究这张A4 纸的运动变化，通过平面平移出长方体、旋转出圆柱等立体图形，学生又一次经历了动态想象、体积计算、直观观察的过程，同时他们在理解“沿着长方形的一条边旋转一周”时引发了矛盾冲突，全班学生在思考中意识到要考虑沿着长边旋转和沿着宽边旋转这两种情况，进一步促进学生养成仔细审题的习惯，学会全面地思考问题。前面一个环节中学生能够用眼睛对比出两个图形的大小，但是在最后的眼见为实环节中却无法用眼睛比较出图形的大小，教师引导学生需要精确计算得出结论，体现了数学的严谨性和严密性。】

片断三：局部旋转，学会理性地数据验证。

1.长方形里面三角形的旋转。

师：还是这张A4 纸，沿着它的对角线分成了图形A 和图形B，请问哪个图形的面积比较大？

生：一样大。

师：一眼就看出来了，A 和B面积相等。现在沿着这张A4 纸的宽边旋转一圈，图形A 旋转出来的图形和图形B 旋转出来的图形哪个大，还是一样？请你把理由写下来。

生1：图形A 和图形B 旋转都是立体图形，看起来图形B 大。

生2：如果图形A 和图形B 一起沿这张A4 纸的宽边旋转是圆柱，图形A 旋转出来的图形是和圆柱等高的圆锥，而圆锥体积是整个圆柱的三分之一，剩下是图形B的体积了，图形B 的体积是圆柱的三分之二，所以图形B 大。

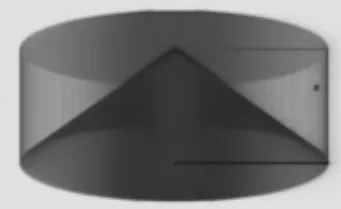
师：那图形B 的体积是图形A 的体积的几倍？

生：图形B 的体积是图形A的体积的2 倍。

师：现在我们眼见为实……

2.三角形的旋转。

师：现在我们只研究图形A，沿着其中20 厘米、30 厘米和36厘米的一条边旋转，你觉得沿着哪条边旋转的图形体积最大？我们先直观地猜一次，（学生都认为沿着最长边36 厘米旋转的图形体积最大）这次大家的意见很一致。大家赶紧精准地计算一下这个图形的体积，最后结果可以保留π。

师：四人小组讨论一下，很多同学认为沿最长边36 厘米旋转出来的图形体积最大，但是大家计算的时候遇到了很大困难，商量一下到底怎么算这些图形的体积。

师：沿着边长20 厘米和30厘米旋转出来的这两个图形体积都没问题，但是沿着边长36 厘米旋转出来的是什么图形？

生：两个圆锥。

师：我们展示一下，看看是否与你们想的一样。这个高怎么算？它的体积是多少？

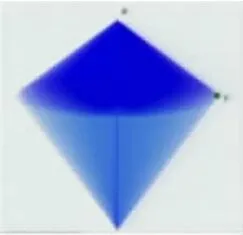
师：6000π、4000π、3468π，同样一个三角形沿着不同边旋转，得到的三个图形的体积是不一样的。没想到沿着最长边旋转得到的图形体积反而是最小的。今天，如果让你分享经验，什么决定旋转出来的体积是最大的？

生：因为它的底面半径是r 的平方倍，高只乘1 次，所以底面半径是决定因素。

师：如果把这张A4 纸进一步转化，比如再剪掉一块，那变化出来的图形就更多了。在生活中，薄薄一张A4 纸蕴含的数学问题真多，只要注意观察，生活中很多的数学问题都等待着你去解决。

【赏析：唐老师在设计教学时具有层次性，从研究A4 纸的整体到局部，符合学生的认知规律；数学知识的难度也逐渐增强，从最初的眼见为实到这个环节的眼见未必为实，利用不同的图形和创设丰富的活动帮助学生从图形变换的角度去计算立体图形的体积，在解决问题中启发学生智慧，发展空间想象能力和直觉观察素养。

当然，“三角形的旋转”属于拓展延伸内容，蕴含的思维含量超出了部分学生的接受水平；而且由于受A4 纸材料和学生的计算水平所限，这里的数据30 厘米、20 厘米、36 厘米都采用了近似数。但是，这个环节在唐老师层层抖包袱的过程中，学生从自信地认为沿最长边旋转出来的体积最大到计算沿最长边旋转图形体积遇到困难，再到惊讶于发现沿最长边旋转的体积最小的过程中反思旋转图形的体积与什么有关，进而从数学本质上掌握了与旋转半径和旋转图形的面积有关。】

回顾整节课的教学，唐老师在这节数学拓展课中充分用足了单一情境素材A4 纸，同时利用几何画板这个现代信息技术，不仅为教学活动提供了丰富的学习资源，还形成了生动的教学形式。在解决有关A4 纸的数学问题过程中，唐老师由线到面、由面到体带领学生产生一系列数学问题，有利于提升学生的探究热情、开阔学生的数学视野、激发学生的空间观念。这节数学拓展课，唐老师的教学设计不仅承载着数学知识的应用和拓展，还承载着学科育人的价值：让学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界，最终促进学生在抽象思考中形成几何直观，发展空间观念和推理意识，真正让数学核心素养在数学拓展课上落地生根，成为每个学生既喜爱又有收获的数学学习活动。