从『模糊认识』到『深度理解』——《小数的初步认识》教学实践与思考（二）

文 杨 通

【教学内容】

人教版三年级下册第七单元第一课时。

【教前思考】

一、学生有哪些模糊的认识

学生对小数有很丰富的经验，特别是在用小数表示价格时。前测显示，所有学生都知道用“元”作单位的一位小数的实际意义，比如学生知道1.3 元就是1 元3 角。但涉及到长度单位时，正确率有所下降；当问到1.3 小时时，几乎所有学生都认为是1 小时3分或1 小时30 分。显然，学生的经验是不成系统的，学生对于小数的认识是模糊的。基于这样的现状，我们认为明晰“十分位与个位之间的十进关系”是改造经验的关键所在。

如何更加有效地进行改造，让学生对小数有更清晰、深刻的认识？不同教材采取了不同路径。

二、不同版本教材的学习路径分析

本课时的教学内容编排采用了如下的逻辑路径：

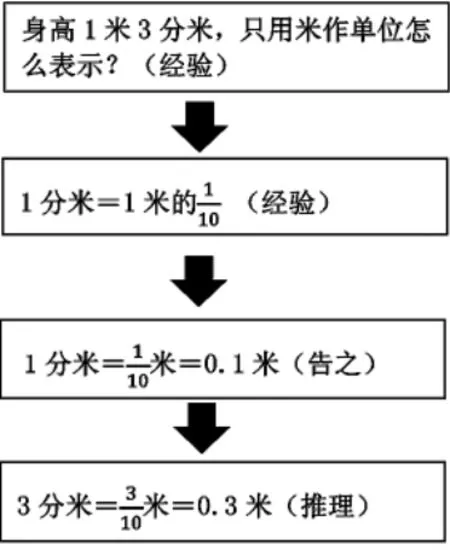
在后续的“做一做”环节中，安排了人民币情境。

以人民币的情境贯穿整个单元。先出示用小数表示的价格，让学生凭经验解释每个小数的含义，广泛激活、充分改造人民币中的小数经验，明确“个位表示元，十分位表示角，百分位表示分”。分数并不出现在本单元中，“0.1就是十分之一”这一内容安排到了“小数的意义”中进行教学。

这是两种典型的编排思路，它们之间的最大区别就是对“分数”与“小数”之间的关系处理以及在引入、展开、巩固阶段的情境选择。

区别一：分数在认识小数中的价值定位。

人教版把分数作为小数初步认识的基础，而北师大版通过直接改造经验来初步认识小数。正如上文所述，本节课的重点是“明晰个位与十分位之间的十进关系”，而这种关系最简洁的表述就是，所以需要把分数作为认识小数的基础。但另一种思路是，小数的初步认识重在经验改造，有无并不会影响对小数的本质认识，这种更为形式化的理解可以安排到小数的意义中去。

区别二：用人民币情境还是长度情境？

人教版以长度作为主要情境；北师大版以人民币作为主要情境。这是两个层次的情境，人民币情境，学生的经验更加丰富，理解更加容易；长度情境对学生而言相对陌生，但更加直观，有利于后续进一步深入学习。可以说各有千秋。

基于对学生学情的分析和不同版本教材的解读，本课的总体设计思路如下：

环节一：通过对学生原有关于人民币经验的改造，明确“0.3元就是把1 元平均分成10 份，取3 份”。

环节二：通过经验改造和类比推理得出“0.3 米就是把1 米平均分成10 份，取3 份”。

环节三：借助长度情境，认识更多的小数。

环节四：通过学生自主探索更为丰富情境下的0.3 的意义，明晰、巩固0.3 就是十分之三。

【教学过程】

一、激活经验，导入新课

师：听说过小数吗？在哪里见过小数？

生：除不尽的时候，有时候用小数表示；表示身高的时候常常用到小数；超市的小标签上有小数。

师：小数常常用来表示价格。

二、改造经验，展开探索

1.认识人民币中的小数。

●环节一：认识0.3 元，明确十进关系。

师：现在杨老师要在黑板上写一个用小数表示的价格，看你认不认识它。

（教师范写小数“0.3”并介绍写法和读法）

师：你知道0.3 元是多少钱吗？

生：3 角。（大屏幕出示3 角）

师：这就是3 角，又叫0.3 元。如果再增加1 角是几元？再增加1角呢？……1 元里面有10 个1 角，0.3 元就是这一部分。（出示下图）

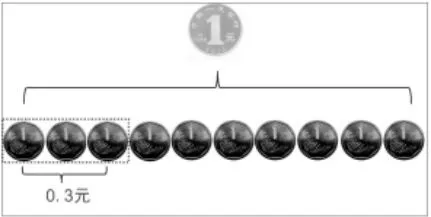
师：看到这个图想到了什么？

生：这其实就是十分之三。

生：10 个1 角硬币是1 元，拿出其中的3 份，就是十分之三。

●环节二：强化认识十进关系。

师：课前我们做过一个小调查，（投影出示下图）如果1 个正方形表示“1 元”，那么哪幅图表示的才是“0.3 元”？下面这些答案对吗？

生：方法三只平均分成了9份，所以不对。方法二平均分成了很多份，也不对。

师：方法一、四分得方法不一样，为什么都是对的？

生：因为都分成了10 份，而且取了其中的3 份。

2.探究长度中的小数。

●环节一：类比推理，认识0.3 米。

师：如果0.3 后面的单位是米，利用刚才学习0.3 元的经验，想一想0.3 米究竟有多长？

（学生借助米尺进行独立思考，互相交流。请学生上台在米尺上指一指。学生上台指向了3 厘米，后来又指向了30 厘米）

师：你为什么有这样的转变？

生：我原来以为是3 厘米，后来想到0.3 米应该是30 厘米。

生：首先要把1 米平均分成10 份，取3 份，那么10 厘米就是1份，3 份就到30 厘米了。

（教师画图并板书：把1 米长的线段平均分成10 份，取这样的3 份）

师：如果让你写一个分数，你会写哪个分数？

●环节二：借助数轴，认识长度中的其他小数。

（1）巩固长度中的十进关系。

出示：0.1 米、1.3 米。先独立在米尺上找一找，再上台交流。

（学生找出0.1 米，教师要求学生从0.1 数到1.0）

师：1.3 米又在哪里呢？

生：找不到了，这里只有1 米。

生：1.3 米应该在1 的后面。

（学生上台估计1.3 米的位置。教师补画线段，并强调后面再增加3 个0.1 米）

（2）比较小数的大小。

出示下图，学生填空。

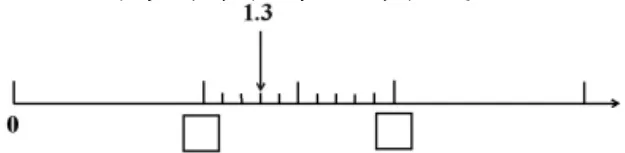
生：1 和2。

师：1.3 大还是2 大？为什么有两个数字的1.3 还是没有只有一个数字的2 大？

生：2 就是2.0，只要看小数点前面的数就够了，2 比1 大，所以2.0 比1.3 大。

生：如果一个数的第一位数比另一个的大，那么就可以比较哪个大了。

生：1.3 就是1 米加上0.3 米，2 米有2 个1 米。

（3）综合练习。

师：在数轴中找一找0.3、2.7 在哪里？

（学生指认，教师出示十等分进行验证）

三、拓展情境，丰富认识

师：刚才我们一起研究了0.3 元、0.3米，那么0.3 后面还可以带什么单位呢？

生：0.3 毫米、0.3 厘米、0.3 角、0.3 千米、0.3 时……

师：请你选择一个单位，画图表示出它的意思。

生：0.3 分米就是把1 分米平均分成10 份，取其中的3 份。0.3 分米用整数表示就是3 厘米。

生：1 千米就是1000 米，0.3 千米就是把1000 米平均分成10 份，取其中的3份，就是300 米。

师：0.3 千米为什么不是3 米，而是300 米？

生：1 千米平均分成10 份，每份是100 米，3 份就是300 米。

生：不管0.3 后面带什么单位，都是平均分成10 份，取3 份。

师：如果是0.3 时，那么应该等于多少分钟呢？

生：3 分钟。

生：我觉得应该是18 分钟。

生：我也认同18 分钟，因为把60 分钟平均分成10 份，每份应该是6 分钟，3份就是18 分钟。

师：不管0.3 后面带什么单位，都是要平均分成10 份，取3 份。所以0.3 用一个分数来表示就是？（板书：）

四、小结延伸，发散思考

（略）