凸显计数结构 沟通数量联系——以《1000与10000》为例

文|吕琼华 张 锋

“数的认识”的学习分成几个不同的阶段，其中“万以内数的认识”不同版本教材都安排在二年级下学期进行学习，但在编排顺序上有较大的不同。大部分教材是先认识1000 和三位数，再认识10000 和四位数。浙教版《数学》则是先认识三位数，再认识1000 和10000，最后认识四位数。经过先前的学情分析，我们制订了《1000和10000》一课的主要教学目标：在个、十、百的基础上认识两个新的计数单位，初步建立起个级的基本结构，为认识更大的数做好准备；将认数和计算以及量感的发展相结合，多角度理解和交流数的意义，发展数感。

【教学过程】

环节一：多元表征，认识1000

1.直观感知。

（1）依次出现小立方体，学生数数：1，10（以1 为单位，呈现10个1），100（以10 为单位，呈现10个10），900（以100 为单位，呈现9 个100）。复习已经学过的3 个计数单位：1、10、100。

（2）继续数数：910、920……990，991、992……999（如图1）。说一说，999 里面有几个几？

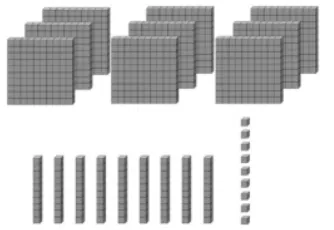
图1

（3）思考：比999 再多1 是几？（动画呈现10 个1 组成10，10个10 组 成100，10 个100 组 成1000 的过程，如图2。）用算式表示并说说是什么意思。（999+1=1000，1000 里面有1000 个1）

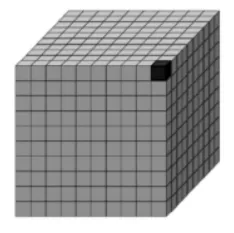
图2

2.建构千位。

1000 和100，10 和1 之间有什么联系？借助计数器找一找它们之间的联系。跟着计数器一边拨珠一边100、100 地数。（100、200……）

引导学生发现：（1）100、100地数，数10 次是1000，10 个100是1000；（2）百位满十向前一位进一，百位的前一位是千位；（3）千位上1 颗珠子表示1 个千。

【评析：学生在认识1000 之前，已经认识了100、10 和1 这三个计数单位，但是并没有系统地将它们进行关联。在认识1000 的过程中，借助学生已有的认数经验，建立1000 与学过的计数单位之间的关系，自主建构千位，逐步建立个级的计数结构，为以后进一步学习十进关系奠定基础。】

3.数数活动。

（1）多角度数数。

师：100、100 地数，数10 次是1000，1000 还可以怎么数？

（2）用算式表示。

全班交流：一位同学数1000，其余同学边听边思考：①他是怎么数的？②数了几次，把数法用算式表示。

根据不同的数法，板书：

100×10=1000；200×5=1000；250×4=1000；500×2=1000；1000×1=1000……

（3）观察与发现。

师：仔细观察算式，你有什么发现？

生：第一个乘数越来越大，第二个乘数越来越小，但是结果都是1000。

生：数的单位越大，数的次数越少；数的单位越小，数的次数越多。

师：非常好，如果以300 为单位数数，你还能用算式表示吗？

生：300、600、900，1000。 以300 为单位不能直接数到1000，数3 次是900，再多100 是1000，300×3+100=1000。

4.自主表征1000。

（1）还能怎样来表示1000？

900 +100 =1000；800 +200 =1000；700+300=1000；600+400=1000；500+500=1000……

（2）交流。

师：你是怎么知道600+400=1000 的？结合数的意思来说一说。

生：600 表示6 个100，400表示4 个100，合起来是10 个100，也就是1000。

师：这些算式有什么相同的地方？

生：都是几百与几百合起来得到1000。

生：不管这两个数是几个百，合起来都是10 个100。

【评析：这一环节以数数活动为载体将认数和计算相结合，用不同的方式表征1000。在表征的过程中赋予每一个数以意义，通过理解几个几、几个几多几、合并等关系，更深入、更全面地认识1000。】

5.小结。

想一想，我们是怎么研究1000的？（引导学生回顾，把1000 和学过的100、10、1 进行联系，借助数数、列算式、分析算式来研究）

环节二：学法迁移，探究10000

1.刚才我们通过数一数、写算式想意思的方法认识了1000，如果我们以1000 为单位来数数，你会数出哪些数呢？请你数一数。

2.你能用学习1000 的方法来研究10000 吗？两人一组进行研究，并把研究成果记录在《学习单》上。

3.学生活动。

4.研究成果交流。

（1）构建万位。

利用计数器，以1000 为单位边拨珠边数数。得出：千位满十向前一位进一，产生新的计数单位——万，得到10 个1000 是10000。

（2）多元表征10000。

呈现学生作品（图3、4），组织学生交流：①这些表示方法正确吗？②哪几种表示方法是有联系的？为什么？③哪些方法是将10000和其他计数单位进行了联系？

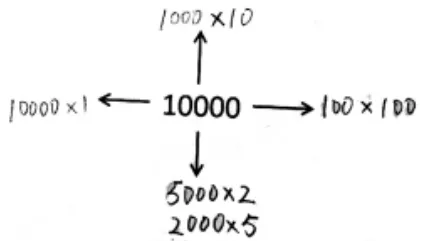
图3

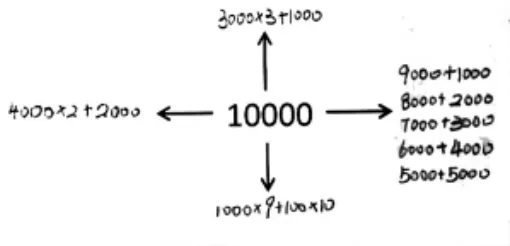
图4

【评析：有了1000 的学习方法和学习经验，学生在自主学习10000 的过程中就有了方向和策略，通过计数器关联相邻计数单位的关系；借助数数活动多元表征，感受到可以用相同计数单位表示10000，也可以用不同计数单位来表示，但是最终表示的意义都是一样的，以此获得对数意义全面而又深入的理解。】

环节三：操作实践，建立量感

1.小实验：1000 粒黑米有多少？

（1）交流讨论。

师：我们认识了1000 和10000，你觉得这两个数有多大呢？

生：很大很大。

师：你能估计一下，1000 粒黑米或者10000 粒黑米会有多少呢？10000 张纸叠起来有多高呢？

生：1000 粒黑米可能会装满一个大箱子。

生：1000 粒黑米可能要装一麻袋。

生：10000 粒黑米可能会堆满一个教室。

生：10000 张纸叠起来，可能有几层楼房这么高。

师：到底是不是这样呢，我们一起做个实验，看看1000 粒黑米到底有多少？四人小组讨论，可以怎么得到1000 粒黑米？

（2）确定方法。

方法1：1 粒1 粒数，数出1000 粒黑米。

方法2：先数出100 粒，这样的10 份就是1000 粒。

组织学生讨论后，采用方法2进行实验。

（3）合作实验。

数一数：小组合作，数出100粒黑米倒入量筒。

估一估：1000 粒黑米可能在量筒的哪个位置，说说理由。

倒一倒：又快又安静地倒入约1000 粒黑米。

（4）交流讨论。

师：10 个小组的量筒都放在讲台上了，你觉得哪些小组得到的大约是1000 粒黑米？你是怎么想的？

生：我们数出100 粒黑米刚好是量筒刻度的一大格，装10 大格就是10 个100，10 个100 是1000。（根据学生发言，出示图5）

图5

师：刚才你们认为1000 粒黑米要用一个大箱子或一个大麻袋来装，现在发现了什么？

生：1000 粒黑米没有我们想象得多，只装了一个小小的量筒，和箱子、麻袋差远了。

2.量感迁移。

师：现在你能估计10000 粒黑米有多少了吗？

生：10 个这样大的量筒，10个1000 是10000。

生：讲台上10 个量筒里的黑米倒在一起就是10000 粒黑米。

（将10 个量筒里的黑米倒入1 个空瓶，如图6）

图6

师：现在你有什么感觉？

生：10000 没我们想象的那么大，10000 粒黑米只有这么小一瓶。

师：请你再思考，10000 张白纸叠起来会有几层楼这么高吗？

生：我们只要知道100 张白纸的高度，就可以推测出10000张白纸的高度。

师：你能从这里找到推测的依据吗？（出示一包A4 纸）

学生观察后发现，一包A4 纸有500 张，测量可得高为5 厘米，从而推算出10000 张白纸叠起来有20 包A4 纸这么高，大约100厘米，也就是1 米左右。

【评析：从学生的发言中可以看出，最初学生对1000 和10000的量感是很弱的，只能用“很大”来表达，也无法较为准确的估计1000 粒或者10000 粒黑米的多少。在操作活动中，学生经历了“数出100 粒黑米、根据‘10 个100 是1000’推测1000 粒黑米的量、再根据‘10 个1000 是10000’合并得到10000 粒黑米”的过程，积累了数学活动经验，也获得了估计的方法，发展了推理能力。量感的建立除了经验，方法也很重要：先估计一份的量，再以这一份为标准去估计几份的量。在这节课中，量感建立的过程也是学生对数意义的进一步理解和生活应用。】

环节四：深入辨析，发展量感

师：现在你能再来说说你对1000 和10000 的认识吗？

生：1000 和10000 其实很小，10000 粒黑米就这么一瓶，10000张纸叠起来还没有我高。

生：我不同意，10000 粒黑米确实不多，但是10000 个人、10000 个足球就多了。

师：你们能想象10000 个人有多少吗？

生：我们教室坐了40 个学生，如果把桌椅拿掉，应该可以站100 个人，那么10000 个人需要100 间教室。

师：你很会思考，从100 个人有多少去推算10000 个人有多少。为什么10000 有时候很小，有时候却很大呢？

生：因为1 粒黑米很小，1 个人却很大。

师：看来10000 在生活中是大还是小，取决于——

生：这个“1”是大还是小。1大，10000 就大，1 小10000 就小。

师：原因是什么呢？

生：因为10000 里面有10000个1。

【评析：“量感也包括在实际背景中提到一个数时能将其与现实背景中的数量联系起来，并判断其是否合理”。学生对10000 粒黑米和10000 张白纸已经有了实际感知，这一环节教师组织学生进一步进行辨析，引导学生发现10000的大小要和生活中的“1”联系起来，这其实也是建立单位观念、进行单位累加的过程，学生在这个过程中进一步丰富和完善对1000和10000 的认识，发展量感。】