借关联知整体 因说理而深刻——《三角形》单元教学中的深度学习策略

文|金雷杰 周 蕾

深度学习是与孤立记忆和非批判性接受知识的浅层学习相对的一个概念，强调学习者积极主动地学习，灵活熟练地运用知识解决实际问题。因此，深度学习的主要特征是关注本质而非表面、实质而非形式、联系的而非孤立的理解，关注应用与创新而非记忆与模仿，最终促进学生高阶思维的发展。

数学课堂要实现真正的深度学习，一方面要寻求意义与知识、经验的链接，沟通概念间的联系，探讨共同的范式与原理，建立整体、全面、深刻的认识；另一方面，不仅要知其然，还要知其所以然，强化证据的检验与讨论的批判性，防止碎片化的学习内容和简单记忆与再现的学习方法，防止无意义、跟从式的学习。

基于以上观点，下面来谈谈《三角形》单元教学中的深度学习策略。

一、《三角形》单元教学中的主要问题

1.碎片化的内容安排，缺乏知识间的内在联系。

四年级《三角形》单元是学生系统学习三角形知识的开始。所涉及的知识点如下：

三角形的特性（三角形的概念、三角形各部分名称、三角形的稳定性、三角形任意两边之和大于第三边）。

三角形的分类（按角分可以分为锐角三角形、直角三角形和钝角三角形；直角三角形中斜边最长；认识等腰三角形、等边三角形）。

三角形的内角和（三角形的内角和是180 度、四边形的内角和是360 度）。

无论是教材编排还是实际教学中，“三角形认识”的各知识点的学习都存在碎片化、孤立化的现象。比如三角形的各部分名称：角、边、顶点之间没有建立必要的联系；又如等腰三角形和等边三角形中，边与角对应的相等关系也没有建立必要联系等。这种现象造成学生对这些概念和特征的浅层理解和孤立记忆，不利于学生形成对概念本质的理解。

2.表面化地理解规律，缺少说理和论证。

教材的意图是让学生发现直角三角形中斜边最长。这个规律的发现是通过测量一个直角三角形的各条边的长度发现的，即使测量多个直角三角形，所得的结论也仍不具有一般性和说服力。其实斜边最长，学生通过直观观察就能感觉到，他们缺少的是斜边最长的道理。本单元中还有三角形的稳定性、三角形内角和以及等腰、等边三角形关系的理解，学生往往都停留在知识表面，缺少必要的推理和证明，也错失了发展学生数学核心素养的好时机。

二、《三角形》单元教学中的深度学习

几乎所有的平面图形的认识都是从研究图形的边和角开始，三角形也一样。从小学阶段的基础认识到初中学习全等、相似三角形，到高中的三角函数，探索的都是三角形边和角之间的规律。因此，三角形的边和角之间本身存在必然联系，不能割裂。同时，作为系统学习三角形的起始内容，《三角形》单元教学还肩负为后续深入学习三角形相关知识积累基本的数学活动经验的任务。所以根据四年级学生特点适度沟通边和角的联系是必要的，也是可行的。

1.加强边和角的关联。

（1）三角形各部分名称教学中边和角的关联。

先来看一则教学案例：

……

师：有谁知道三角形各部分名称？上来指一指、说一说。

（学生尝试）

师：是的，三角形有3 个顶点，3 个角，3 条边。

（板书：3 个顶点，3 个角，3 条边）

师：用大写字母A、B、C 表示这个三角形的3 个顶点，这就是三角形ABC 了。3 个顶点分别是顶点A、顶点B、顶点C，3 个角分别是∠A、∠B、∠C，3 条边分别是AB、BC、AC。

大多数教师到这一步就把三角形各部分名称的教学完成了，显然这些概念之间是孤立的、不相关的，造成学生的机械记忆，也不利于后续学习。此时，正是教师对三角形的顶点、角和边三者进行必要的沟通和关联的好时机。

师：（在黑板上边指边说）请同学们继续观察这些顶点、角和边，顶点A 所在的角是∠A，∠A 的对边是BC，它们是一组好朋友。

（板书：点A ∠A BC）

师：你还能在三角形ABC 中找到这样的对应关系吗？

根据学生回答，完整板书如下：

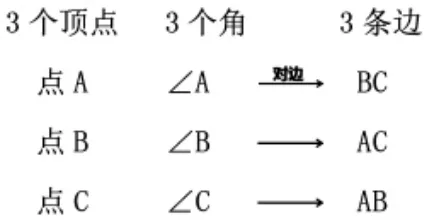
这样，既为后续学习作“高”时的“对边”提前铺垫，也使三角形中的顶点、边和角建立有机联系，形成完整的知识链。

（2）特殊三角形教学中边和角的关联。

三角形按边分类的教学环节一般是这样设计的：

师：关于等腰三角形和等边三角形的知识有哪些呢？请同学们自学课本第64 页。

师：你能向大家介绍一下吗？

学生介绍：

①有两条边相等的三角形是等腰三角形，三条边都相等的三角形是等边三角形。

②等腰三角形各部分名称、等边三角形各部分名称。

③等边三角形是特殊的等腰三角形。

教师在黑板上的等腰三角形和等边三角形上分别标注各部分名称。

师：等腰三角形和等边三角形还有什么特点呢？请同学们量一量、折一折，看看有什么发现？

得出：等腰三角形两个底角相等；等边三角形三个角都相等；等腰三角形和等边三角形都是轴对称图形。

教学到此结束，学生虽然已经比较全面地知道了等腰、等边两种特殊三角形的特点，但这两种特殊三角形边和角的特点各自独立，还是割裂开来的，边是边的特点、角是角的特点，边和角之间没有建立关联。此时，教师只要稍微进行延伸和拓展，教学效果就完全不一样了。

师：请同学们继续观察等腰三角形的腰和底角，你又有什么新的发现？

生1：腰和底角是相对的。

师：你能上来指一指吗？

生2：我还发现，腰相等，所以相对的底角也相等。底边和腰不相等，所以顶角和底角也不相等。

师：把边和角联系起来看是我们研究三角形的好方法，你能用这样的眼光再来看看等边三角形吗？

生3：我知道了，因为等边三角形的三条边相等，所以三个角也全都相等了。

师：看来边和角之间确实有紧密联系，让我们再回过头来看看我们研究过的钝角三角形和直角三角形吧。

生4：我发现钝角三角形中钝角所对的这条边最长。

生5：我发现直角三角形中直角所对的斜边最长。

生6：我发现三角形中长边对大角，短边对小角，它们是相互关联的。

虽然只是在原来教学基础上增加了一个边和角沟通的小环节，但学生对三角形边和角的认识却迈出了一大步。学生不仅认识了各种特殊三角形的边和角各自的特点，而且建立了边和角的联系，使边和角之间产生因果关系，直接指向三角形特点的本质，真正实现了融会贯通、深度理解。

（3）不同分类标准下各类三角形之间的关联。

三角形按角分，可分为三类，分别是锐角三角形、直角三角形、钝角三角形；按边分，可分为两大类，即三条边都不相等的三角形（一般三角形）和等腰三角形，其中等腰三角形又可分为一般等腰三角形及等边三角形。三角形的分类教学仅限于此是不够的，应用关联的眼光看待不同分类标准下的各类三角形，结合边与角的因素，边想象边连线，如下图所示，在沟通不同类三角形之间关系的同时，丰富学生头脑中三角形形状的素材库。同时，通过适时追问“等边三角形会是直角三角形或钝角三角形吗？”“等腰直角三角形3 个角的度数有什么特殊之处？”进一步挖掘等腰直角三角形、等边三角形这些特殊三角形边、角的特点。

2.适度进行“所以然”的解释。

小学数学教学中，教师往往只关注“是什么”，而不关注“为什么”，关注“为什么”就是深度学习的具体体现。适度的证明和解释既能加深对知识的理解，又能培养学生的逻辑推理能力。教学中把所要学习的知识与原有知识进行关联，并加以解释是开展深度学习的常用方法。

（1）三角形稳定性的解释。

用这样的3 根小棒，搭三角形；用这样的4 根小棒，搭平行四边形。

你有什么发现？

……

三角形中，确定3 条边的长度，只能得到一种形状的三角形，形状不会变，这就是人们常说的：三角形具有稳定性。

而平行四边形呢，确定4 条边的长度，能得到无数种不同形状的平行四边形，形状不能确定，所以我们常说，平行四边形容易变形。

一般，教师到此就结束三角形稳定性的研究，马上进入稳定性应用的环节。其实利用学生搭三角形的经验继续追问：为什么3 条边确定了，三角形的形状也就确定了呢？学生虽然不能规范说理，但通过操作和讨论能够得出：用两条边搭出的是角，开口是不确定的，有了第三条边，就把原来的开口给固定了，因此三角形的形状是唯一的、固定的。三角形的唯一性决定了三角形的稳定性。这样的教学可以使学生更深刻地理解三角形的唯一性，也能更好地理解在实际生活中稳定性的应用。

（2）直角三角形中斜边最长的解释。

前文中已提到过，课本是用测量的方法让学生发现直角三角形中斜边最长，对四年级学生来说，略显幼稚且不具说服力和一般性。其实完全可以利用四年级学过的“直线外一点向这条直线所作的垂直线段最短”这一性质来解释说明（如下图）。

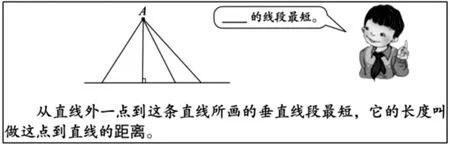
先让学生观察下图，你觉得哪条边最长？能利用原有的知识来说说为什么吗？部分学生经过思考能够回答。

因为点A 与线段BC 所作的两条连线AB 和AC，AB 是垂直线段，所以AC 比AB 长；同理,BC 是点C 向线段AB 所作的垂直线段，所以AC 比BC 长。由此得到直角三角形中斜边最长。这样得出的结论具有一般性，适用于任意直角三角形。

通过说理，学生不仅深刻理解了直角三角形中斜边最长的特点，而且培养了学生演绎推理的能力,发展了学生的数学核心素养。

（3）等边三角形是特殊等腰三角形的再解释。

早在三角形分类的教学中，学生就已经基于定义知道了等边三角形是特殊的等腰三角形，从边的特点理解两类三角形的关系：等腰三角形中如果第三条边也相等就是等边三角形。而这两类三角形之间的关系，还可以从角的特点加以理解，在“三角形内角和”的教学之后，教师设计了如下探究问题，引导学生证明说理。

师：我们知道等腰三角形仅两条边相等，而等边三角形需三条边都相等，也就是，若等腰三角形增加“第三条边也相等”的条件，就是等边三角形。这是从边的特点说明了等边三角形是特殊的等腰三角形。那么，从角的特点思考，等腰三角形增加什么条件，就能变成等边三角形呢？

生：（脱口而出）三个角都是60°。

师：真要这么多吗？少一些可以吗？大胆猜想一下，最少增加几个60°的角，等腰三角形就变成等边三角形了？

通过推理计算，学生发现只需知晓一个角是60°即可，即有一个角是60°的等腰三角形，就是等边三角形。分类思考可知：若60°角是等腰三角形的顶角，则两底角度数为（180°－60°）÷2＝60°，三个角相等，都是60°，可知三条边也相等，该三角形为等边三角形；若60°角是等腰三角形的底角，则顶角度数为180°－60°×2＝60°，同样可知该三角形为等边三角形。在这个过程中，学生应用已有的内角和知识、三角形边角之间的关系，不仅对等腰、等边三角形的包含关系有了更深入的理解，更为重要的是经历了一次难得的推理与证明过程。

虽然小学阶段大多是通过归纳、类比等合情推理方式让学生发现规律，但像这样适时地利用原有知识基础或生活经验对发现的结论进行说理或解释，进行必要的演绎推理，不仅能加深对知识的理解，发展学生的推理能力，而且还能主动与初中教学衔接，培养思维的逻辑性、条理性，提升思维品质，减少小升初后的不适应。

总之，加强知识间的关联，用联系的眼光来学习、观察，学会用已有知识和经验来解释发现的结论，既是完整深刻掌握知识、学会学习的需要，也是开展深度学习、发展学生数学核心素养的正确途径。

栏目介绍

【教学策略】透视教学现象，探寻教学方法，求索教学规律。

【典型课例】展示经典课例，领略名家风采；推介成功教例，凸显不同风格。

【教案精选】突出自身教学特点，融合课程理念，让读者有所得、有所思。

【课堂再现】紧扣课标理念，注重实践过程，强调可操作性。

【磨课手记】典型课例的教学改进，一课多教的案例剖析。

【感悟名师】感悟名师教学的精彩设计，领悟课标理念的灵活体现。

【教例反思】探究教学设计的成败得失，反省教学过程的点点滴滴。

【教学一得】教研活动中形成的点滴心得或随笔。