紧扣数数本质 促进概念形成——《小数的初步认识》教学实践与思考（一）

文 王越娟

【教学内容】

人教版三年级下册第七单元第一课时。

【教前思考】

小数亦称十进小数，是实数的一种特殊表现形式。三年级学生对小数已有一定的生活经验，但大多是依附于商品价格、长度、气温等认识，离开这些现实情境，小数便成了抽象的存在，让人难以理解。那么，如何帮助学生更好地认识小数呢？

史宁中教授在《〈数学课程标准（2011年版）〉解读》中指出：“小数产生有两个前提，一是十进制记数法的使用，二是分数概念的完善。”而现行的小学数学各版本教材在第一次“认识小数”时大都强调“小数是十进分数的另一种表示方法”，并沟通了整数、分数与小数之间的联系。人教版教材在“分数的初步认识”学习的基础上，安排了“小数的初步认识”，并以“长度”作为主要的学习素材，试图通过分数意义的迁移来实现学生对小数意义的理解，如“1 分米是米，可以写成0.1 米；3 分米是米，可以写成0.3 米。”但看似“一脉相承”的问题情境，学生在学习过程中却有些“生硬”。为何？因为之前在初次认识分数时，更倾向于对“关系”意义的认知，（如下图）而在初次认识小数时，则更倾向于联系分数的有关“具体量”的意义。同时，学生在对于生活中具体量的体验中，“用分数”的经验并不丰富。因此，仅仅借助分数的“具体量意义”来突破对小数的理解，显得并不恰当。

通过对数学史的了解，我们也发现，相较于分数，小数似乎与十进制计数法更有渊源。而数学家华罗庚早已明确提出“数是数出来的！”他认为：小数是十进分数的简写形式，但简写不是终极目的，终极目的是为了分数也能像整数那样“满十进一、退一作十”。整数、小数、分数因为十进位值、数的数数本质而得到了贯通。因此，我们既要重视并利用好“分数”这一基础对“认识小数”的积极作用，同时更应沟通好计数方法一致的整数和小数。一方面，通过具体“量”的导引帮助学生理解小数的现实意义；另一方面，也要适时放手，让学生尝试用自己的方式去表征和探究小数，主动质疑、实践、感悟和发现。

【教学过程】

一、重温“数数”，激活“计数单位”的经验

1.重温“数数”。

师：同学们，在数数时咱们都请哪些数学工具帮过忙呀？

生：小棒、计数器、圆片、方块等等。

（根据学生的回答，课件出示，帮助学生更好地回忆）

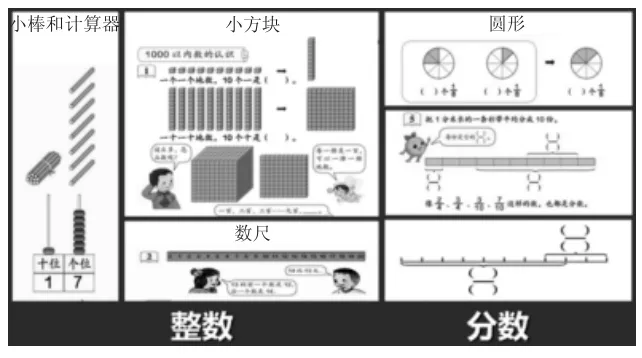
师：是啊，借助这些数学工具我们认识了很多整数和分数，就像我国著名的数学家华罗庚爷爷说的那样：“数是数出来。”今天，我们就来数“小数”。

2.读写“小数”。

师：请在学习纸上写一个小数，并观察有什么特别的地方。

生：都有“小数点”。

师：对，正是这个“小数点”把小数分成了左右两个部分。一起读一读……

二、探究“新数”，促进“计数经验”的迁移

1.提出质疑。

师：（课件出示“0.1”）看到这个小数，你有什么疑问吗？

生：为什么要有0.1？有1 还不够吗？

生：0.1 表示多大呢？

生：0.1 是怎么来的？

生：0.1 和1 有什么关系？

师：大家提的问题都非常值得我们思考，接下来就请带着这些问题来研究这个看似简单又有点神秘的“0.1”吧！

2.自主表征。

师：（出示四种学习材料）请你任选一种或几种材料，表示出“0.1”。

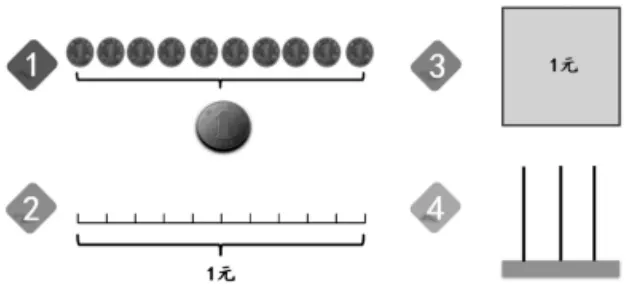
（学生自主表征，教师巡视收集典型素材）

3.交流反馈。

●材料1 反馈：基于“1 角＝0.1元”的经验，借助硬币表征“0.1”。

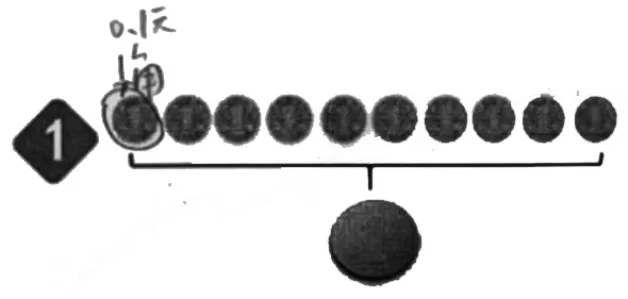
师：他找对了吗？

生：找对了，1 角＝0.1 元。

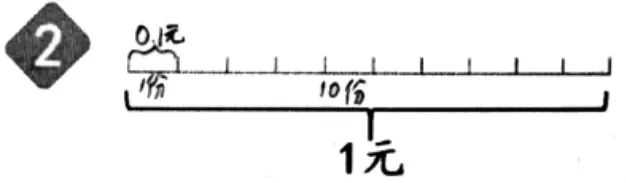
师：为什么这一段表示0.1 元？

生：1 元里面有10 个1 角，这里正好把1 元平均分成了10 份，其中的1 份就表示1 角，也就是0.1 元。

师：在他说的这段话中，有什么值得特别注意的？

师：除了这一段表示0.1，还有没有0.1 了？

生：剩下的每一份都表示0.1。

●材料3 反馈：借助正方形表征“0.1”，关注错例强化“十分”。

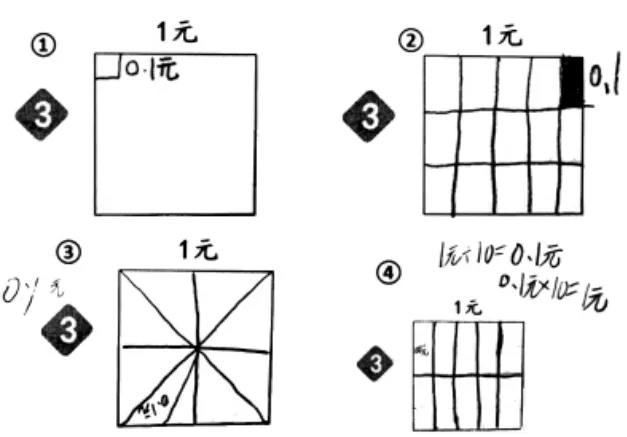
师：仔细观察这几幅图，请大家发表意见。

生：怎么确定①里面画的这一小块表示0.1？

生：按照他这样表示，我估计这里大约有25 个0.1，合起来超出1 了。

生：②和③虽然分了，但一个15 份、一个9 份，而且还不平均，也都不对。

生：我赞同④，他不仅分对了，还写了算式，表示得很清楚。

师：同学们，能不能用一句话来概括自己的判断标准？

生：就是看有没有平均分成10 份。

师：把1 平均分成10 份，其中的1 份还可以用哪个数来表示？

●材料4 反馈：借助计数器表征“0.1”，打通整数与小数的“十进”关系。

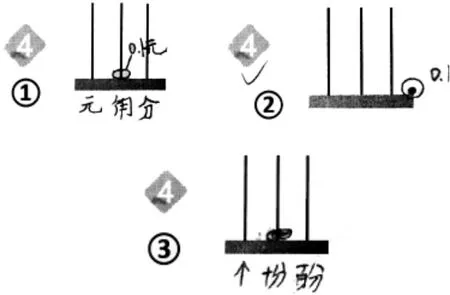
师：看了这些同学的作品，有没有想问的？

生1：我对②有疑问，这个是计数器，你的0.1 怎么在计数器的外面？

生2：计数器的最右边是个位，0.1 比1 小，只有十分之一，所以不能把珠子拨在个位上，只能在个位的右边。

生1：那我们在计数器上再加一根上去不就得了。

生3：我本来看不懂③，现在有点明白了。其实和②是一个意思，只不过③把最左边那个位置看作个位，这样中间一位就可以表示0.1，如果再分下去，还可以继续增加位置，就是他写的百分。

生4：我觉得后面两种表示比第一种更好，不用想元、角、分，也可以表示出比0.1 更小的小数。

师：真的吗？那我们就拿真的计数器来试一试。我们先像③那样把个位定好，一起数一数。

（1、2、3……9、10）

生：满十进一，十位上拨1。

（10、20、30……90、100）

生：又满十进一了，在百位上拨1。

师：如果我想把这1 个百还回去，怎么拨？

生：把百位上的1 拨回去，十位上拨10。

师：要把这1 个十还回去，怎么拨？

生：把十位上的1 拨回去，个位上拨10。这就是退一作十！

师：很好！那现在剩下1 个一，我还想还回去，有办法吗？

生：还是一样，把1 拨回去，个位右边拨10。

师：这里的1 表示多少？

生：0.1。

师：再右边一个位置拨1 呢？

生：0.01。

师：还能再往右退一当十吗？

生：可以呀，数不完的。

师：回顾刚才在计数器上数小数、数整数的过程，有什么发现？

生：数小数和数整数的方法是一样的，每满10 个就要向前进一，反过来，退下来的1 又可以换成10。

生：整数和小数是连着的，它们就像一家人。

4.抽象释疑。

师：（课件回到四种材料）无论在哪种材料里，大家都找到了0.1。那么，现在你对一开始的几个疑问有想法了吗？0.1 是怎么来的？它和1 有什么关系？

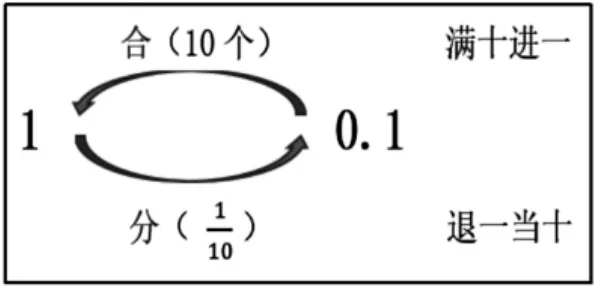
生：0.1 是从1 里面分出来的。

生：0.1 是把1 平均分成10份，表示其中的1 份，也就是反过来10 个0.1 就能合成1 个一。

师：原来，0.1 和1 之间就是这样一种“分与合”的关系呀！你们真能干！

三、拓展“小数”，感悟“计数活动”的本质

1.辨析：是0.3 米吗？

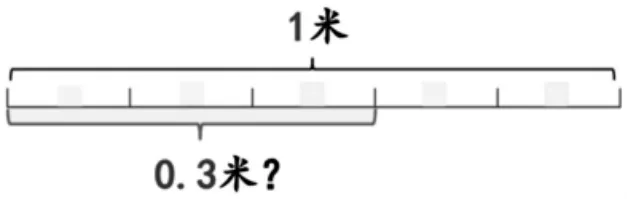
师：请判断并说明理由。

生：不是0.3 米，因为这里没有把1 米平均分成10 份，所以每一份不是0.1 米，3 份也不是0.3 米。

生：在这个基础上继续分，也就是这里的每一份再平均分成2份，就能看出这不是0.3 米，而是0.6 米。

2.拓展：看图直接说出小数。

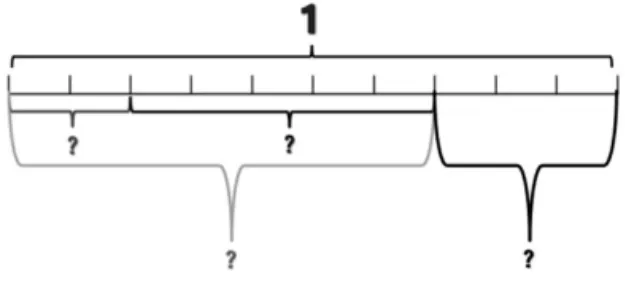
（渗透简单的小数加减法）

3.提升：根据需要合理推想。

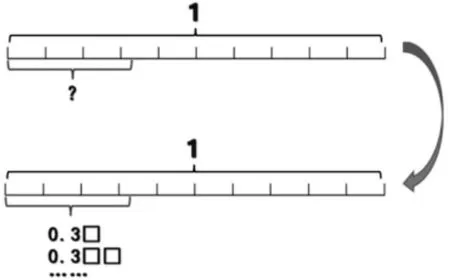
（渗透对两位小数、多位小数及精确度的初步认知）

4.总结。

师：我们数着数着就把这么多“小数”数出来了，数着数着就把“小数”给数明白了。在今天的“数数”活动中，你还有哪些发现或体会吗？

……

师：同学们说得太棒了！其实，今天我们对小数的认识只是冰山一角，往后，我们还将通过“数数”探索和发现更多的小数。