基于趣用的初中数学“综合与实践”活动研究
2022-05-30穆益梅


【摘要】教师在教学的过程中不仅要引导学生获得基本数学认知,同时还要引导他们在学习与生活中运用知识、开展实践,进而培养学生的数学素养。因此教师可开展“综合与实践”活动,让学生在具体的实践活动中结合自身所学的知识积极思考、自主探究,提高解决问题的能力。当教师设置的问题是学生在日常生活中会遇到的,他们就能从趣用出发,揭开生活与数学的内在联系,进而用数学思维解决生活中的实际问题。可见开展基于趣用的综合实践活动,能让学生真正获得成长。
【关键词】初中数学;趣用;综合与实践
作者简介:穆益梅(1982—),女,江苏省海安市城东镇西场初级中学。
学生学习数学的过程也是他们进行各种体验的过程,因此教学中教师要尽可能地让学生进行多方面的体验,以促进他们全方位的发展。也就是说,教师不仅要解放學生的大脑,还要解放他们的双手、双眼,促进学生多元成长。教师开展“综合与实践”活动能给学生提供大胆尝试的平台,给他们动手操作的机会,使他们探究出数学的内在规律。但教师要基于趣用开展“综合与实践”活动,激发学生的潜能,引导他们主动参与。所谓“趣用”就是学生能在“综合与实践”活动中获得乐趣,也获得成长,获得思维上的发展,也获得精神上的满足。
一、设计满足学生需求的“综合与实践”活动
教师设计的“综合与实践”活动要能满足学生的需求,也就是说要能激发他们探究的欲望,要能解决他们生活中遇到的一些问题。数学来自生活,如果教师设计的“综合与实践”活动以生活为蓝本,学生能在活动中回想起他们曾经的经历,就能运用数学知识,享受实践之趣。趣用其实就是为学生的学科素养培养寻找一条路径,能让他们主动建构认知,进而提高能力[1]。
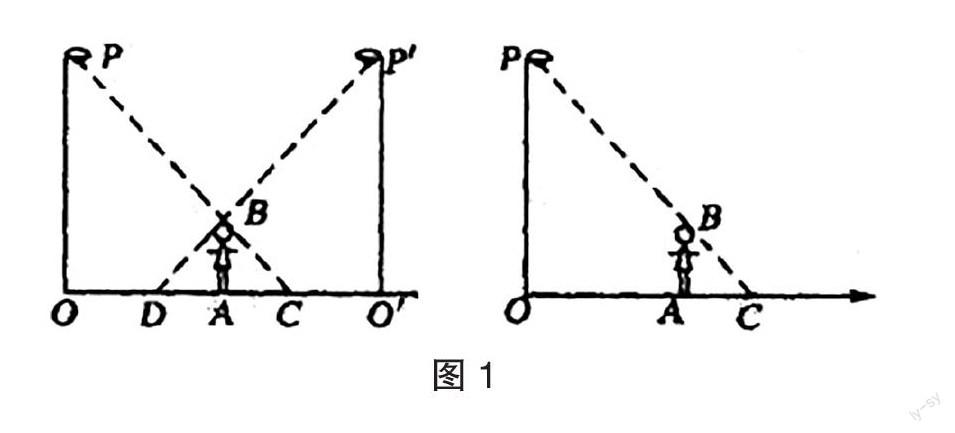
以人教版初中数学九年级上册“相似三角形的应用”的教学为例,这个章节的主要内容是相似三角形定理的运用。教师不应照本宣科,将有趣的实际应用变成枯燥乏味的刷题。因此教师设计了这样的综合实践题:如图1所示,珊珊晚上在校园的路灯下散步,已知珊珊的身高AB = h,灯柱的高OP=O′P′ = 1,两灯柱之间的距离OO ′ = m。假如珊珊距灯柱OP的水平距离OA = a,能不能求出影子AC的长?假如珊珊在两路灯之间行走,那么她前后是不是有两个影子,它们的长度之和DA+AC是不是定值?假如珊珊在点A朝着箭头的方向,即影子的方向,以V1匀速行走,能不能求出她的影子的顶端在地面上移动的速度V2。
对于这道题,教师先带领学生到学校的路灯下,让他们将图中的信息与现实对接起来,将原本抽象的题目变成真实的场景,从而题目中要求的结论也真实地呈现出来。教师先以珊珊为参照,与学生一起将图中的信息用粉笔在地上画出来,这是一个读题的过程,也是实践的过程,更是趣用的过程。学生不再仅仅在草稿纸上完成演算,而是在生活中操作。学生在地面上画出的图,跟图1相同,只是更直观。在推算中他们发现,这两个影子的长度之和竟然是一个定值。接着,教师让学生在路灯下走动,通过亲身体验来感知题目。教师列举的问题是学生每天都会经历的事,探究其中的奥秘俨然是他们感兴趣的。教师把抽象的相似三角形的问题转化为具体的实际问题,学生再趣用相似三角形对应边成比例这一认知使得问题得以解决。因此教师在开展“综合与实践”活动时,要关注学生的生活,从生活中寻找话题,给“趣用”以更多的可能。数学学习的过程就是学生运用所学的知识解决问题的过程,可见学习的重点是落在“用”上的。如果学生对“用”感兴趣,能在“用”中有所收获,他们会乐此不疲地去实践、去探究。可见教师在教学中要关注学生的情感,关注他们的真实需求,以使活动更具吸引力。
二、尊重学生在“综合与实践”中的主体地位
教师采用趣用的方式既能挖掘学生的智力因素,也能挖掘他们的非智力因素,能更好地促进学生能力与素养的提高。基于趣用的综合实践课堂自然需要突出学生的主体地位,要让学生自己体验,体会学习的乐趣。在当前的数学学习中,很多学生感觉不到快乐,主要原因就是教师没有采用正确的教学方式。教师要借助综合实践活动激发学生学习数学的兴趣,增加学生运用数学知识的机会,给他们提供自主学习的舞台。
以人教版初中数学九年级上册“实际问题与二次函数”的教学为例,教师先呈现一张真实的隧道截面图(图2),问学生有没有留意过隧道的样子,以真实的图片激发学生的兴趣。教师接着问学生能不能将截面图建立在坐标系上,再以几何图形的形式呈现出来。学生先是发现隧道的形状是一条抛物线,接着发现地面基地是长方形,因此他们画出图3,在趣用中他们的思维由具体到抽象。教师接着说:“假设长方形的长AB为8 m,宽AO为2 m,隧道最高点P位于AB的中央,距地面6 m。假如一辆高4 m、宽2 m的货车正往隧道行驶过来,你们能不能想出一些问题来。”学生想到的第一个问题是这辆货车能否从该隧道通过,第二个问题是能不能求出抛物线的解析式。但他们在实际运用时,发现要先求出解析式。学生先画图,他们计算出抛物线的顶点坐标为(4,6),因此抛物线的方程可设为y = a(x-4) 2+6。学生发现点A在抛物线上,所以抛物线的解析式为 y =-(x-4)2+6。对于第二问,学生在运算过程中发现货车是否能通过隧道竟然需要计算抛物线两个根之间的距离,体会到生活与数学总是息息相关。教师问学生有没有新的问题可以问,学生根据“假如一辆高4 m、宽2 m的货车正往隧道行驶过来”这一条件,想到了这样的问题:两辆这样的车是否可以通过隧道。他们分析,货车通过的前提是隧道内要设双行道,第二步才是计算|x1-x2|是否大于2,结果是假如隧道内设双行道,两辆这样的货车可
以同时通过。从整个过程来看,无论是画图,还是提问,教师都突出了学生的主体地位,让学生自己去操作、去探究。画图是学生需要掌握的重要的数学能力,也是重要的实践能力。让学生提问改变了学生的学习方式,给予了他们更多的主动权,让他们的能力得以彰显,也让趣用得以落实。因此,学生自己能思考的教师就让他们思考;学生自己能动手的,教师就让他们动手操作。在整个过程中,教师要始终坚持学生是第一位的原则,明确“综合与实践”活动的主体是学生,为学生提供充足的展示机会。
三、抓住生活中偶发的“综合与实践”教育契机
教师要为学生提供实践与体验的机会。在教学的过程中教师可以设计一些实践活动,考虑学生多方面的因素,让活动取得更好的效果。大多数实践活动需要教师想好活动流程、活动计划、活动内容等。但在具体的教学过程中,教师还需要发挥教学机智,抓住偶然的机会,开展实践活动,给学生提供趣用的机会。这种看似无意的举措更能激发学生的兴趣,提升他们的迁移与运用能力[2]。
例如,班级要举办数学与传统文化的演讲比赛,最终决定由5名学生参加演讲比赛。教师问学生谁第一个上台演讲呢,可不可以由教师指派。学生说要以抽签的方式决定每个人的出场顺序,這样才更公平。教师就让学生自己动手操作,他们先是制作了5根形状大小相同的纸签,然后在上面分别标上出场的序号,再将这些纸签放进一个不透明的盒子里。木木第一个抽签,她任意取出一根纸签。本来这时木木将纸签上的数字报出来,第二个学生就可以上台抽签。但教师抓住这个偶然的机会,将实践与趣用联系起来。教师问学生能不能就木木抽到的纸签提出一些问题来,这些问题要包含刚刚学过的不可能事件、必然事件与随机事件。每个学生在座位上也做了几个简单的纸签,抽出了其中一张,并试着提出一些问题。问题有:可能抽到序号是0的纸签吗?这是什么事件;抽到的纸签上面的序号可能小于6吗?这是什么事件;抽到的纸签上面的序号可能是1吗?这是什么事件。每个学生都体验了一次抽签的过程,不光是上台演讲的学生,每个学生都学会了一个小的生活技能,就是用抽签的方式来决定一些事情的前后顺序。本来枯燥的数学学习因为这一实践活动而变得有趣。每个学生在实践中都运用了课本上的知识,将知识转化为能力。在课堂上、生活中偶发的事情比较多,教师要从这些偶然的事情中发掘重要的教学资源,进而丰富学生的综合实践活动。这样能让课堂充满情趣,同时也能让学生在轻松的氛围中获得多方面能力的提升。在教学中教师需要预设教学资源,也需要及时生成教学资源,要抓住学生生成的资源,开展更好的教学。
四、布置“综合与实践”的作业
当前的初中数学作业存在单一、机械的现象,教师布置的作业基本以书面习题为主。这样的模式不利于学生的多元发展,也不利于“双减”政策的落实。“双减”政策要求减少学生的作业量,将学生从题海中解放出来。教师可以布置“综合与实践”的作业,让学生运用多种感官完成作业,增加学生多元体验的机会、即增加他们多方面巩固知识的机会、多方面提升能力的机会。换言之,教师要用少量题目达到之前大量题目才能达到的效果。学生喜欢用纸片折东西,尤其是男生。课间教师经常看到学生折纸飞机、纸炮的场景,因此教师可以将学生的这一喜好与数学上有关折纸的问题联系起来,既体现“趣”,又体现“用”。
例如,教师布置这样的实践操作题,让每个学生拿出一张直角三角形的纸片,在三个顶点处标上 A、B、C,∠ACB=90°,教师让学生将纸片折叠,使点B与点C重合,同时在折痕处标上字母 MN(图4)。当学生这样做了之后,教师问学生能不能从中发现一些规律,比如哪一线段与哪一线段相等。教师的问题一方面促使学生再次实践,在第二次折叠中发现其中的奥秘;另一方面也暗示学生要考虑相关线段之间的关系。有学生发现,折叠之后AM与BM是相等的。学生的“发现”不是坐在座位上凭空想象出来的,而是他们在“趣用”中得出的。因此教师要拓展“趣用”的路径,要让他们在“趣用”中有更多发现。解决这类折纸类实践题最关键的就是学生要能读懂题目,要能将题目的表述以具体的操作展现出来。因此遇到此类题目,教师可指导学生以实践的方式理解题目的内涵。同样,教师需要给学生提供趣用的机会,比如这道题中教师不直接给出结论,让学生证明,而是让他们对比折叠前与折叠后的不同,自己推导出一些结论。“趣用”能体现在猜测中,学生先在“趣用”中发现问题,进而再解决问题。因为有实际操作,学生推导的结论往往容易得到验证,这让他们对接下来的证明充满期待。可见,综合实践作业既改变了学生的学习方式,也改变了教师的教学方式,能促进教师和学生的全面发展。
结语
学有所用,数学学习的目的是让学生能将课堂获得的知识转化为能力,进而运用到实践中。“综合与实践”活动的开展能够促进知识的迁移与运用,学生可在相关的活动中趣用知识,进而促进能力的发展。学生可以在折叠、平移、旋转图形的过程中发现更多数学的奥秘,也可以在画一画、拼一拼、凑一凑、摆一摆的过程中破解题目中的密码。这种活动将兴趣与实践完美结合,能使学生获得全面的发展。因此教师要开展基于趣用的“综合与实践”活动,以激发学生的参与热情,让学生迸发思维的火花。
【参考文献】
[1]蔡庆有.数学“综合与实践”内容的课程分析[J].教学与管理,2017(01):58-61.
[2]斯苗儿.是一个领域,更是一种数学教育价值观:“实践与综合应用”备课解读与难点透视[J].人民教育,2006(17):24-29.
