动态几何：赋予 “空间观念”以生长的力量

任超

【摘 要】“图形与几何”作为数学课程四大板块内容之一，重点培养学生的空间观念。但由于传统教学软件的局限性，教师在教学图形与几何板块时往往因工具而掣肘。笔者以几何画板为依托，结合具体实例，探索讨论动态几何在教学过程中的应用，为教师更好地帮助学生发展空间观念提供帮助。

【关键词】动态几何 几何画板 空间观念

“数学是研究数量关系与空间形式的科学。”空间形式最主要的目标是发展空间能力。动态几何让图形“动”起来，在“运动或变换”中来研究、揭示、学习图形的性质，这样一方面可以加深对图形特征的本质认识、体验几何原理的生长过程;另一方面可以培育数学情感，促进逻辑推理能力和直观想象的能力发展，实现空间素养的提升。

一、审视：“动态几何”教学现状

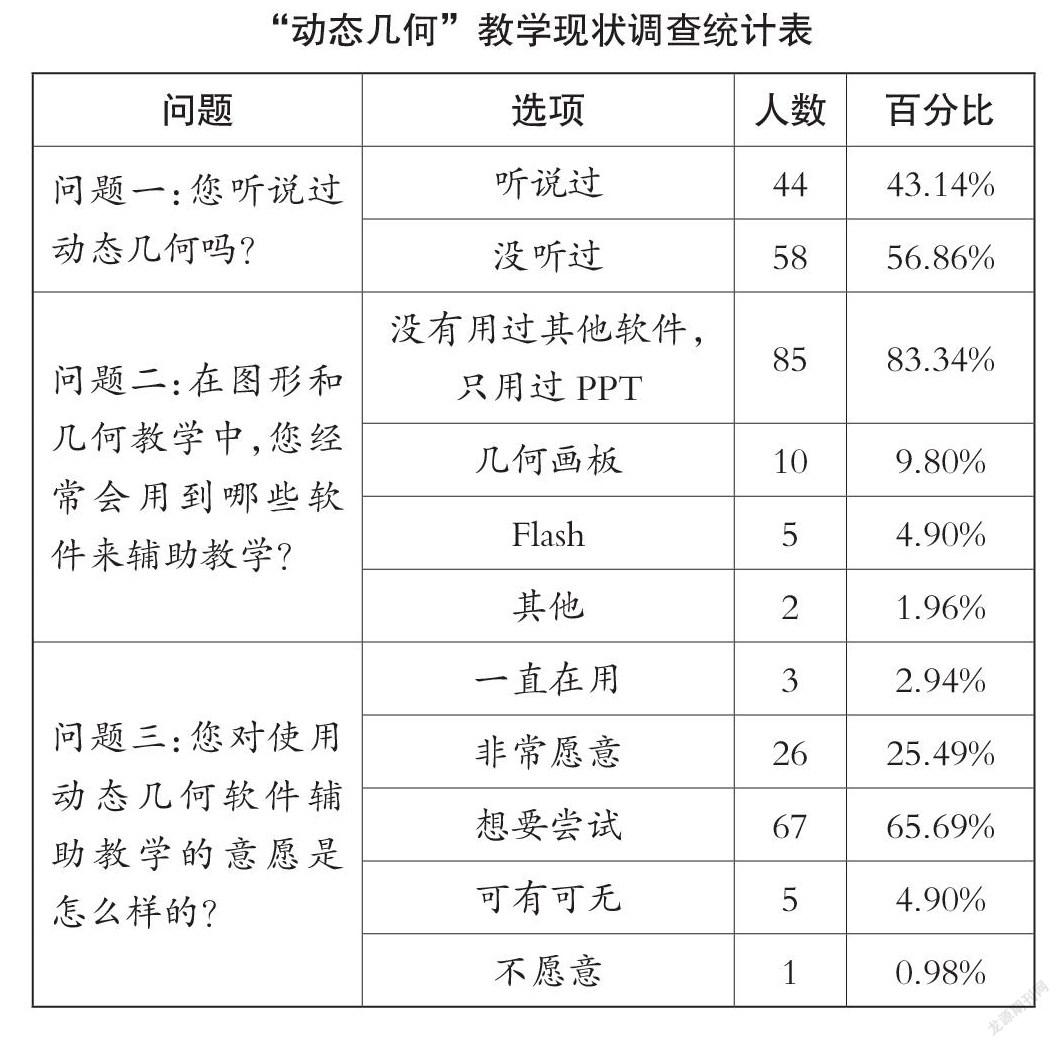
在小学数学课程中，“图形与几何”作为数学课程四大板块内容之一，重点培养学生的空间观念，在这个过程中就不得不提到一项与信息技术相关的策略——动态几何。为了剖析目前小学数学“动态几何”的教学现状及教师对这一概念的认知，笔者通过“问卷”对所在地区的102位教师（其中21位低年级教师、29位中年级教师、52位高年级教师）进行了随机调查，结果如下表。

通过调查统计表，我们发现：

（1）被调查的教师中，一半以上的教师对“动态几何”这一概念不了解;

（2）在平时的图形与几何的教学过程中，大部分教师只采用演示文稿来进行教学，对于其他一些动态几何的软件运用很少。笔者通过与几位被调查的教师谈话发现，出现这种现象的原因大致有这几种：①对PPT的运用比较熟练;②不知道有哪些动态几何软件;③对软件的功能和作用不了解。

（3）“非常愿意”和“想要尝试”运用动态几何软件来辅助教学的教师总和占了总数的91.18%。

综上所述，数学教师因对 “动态几何”认知度不高，缺乏对动态几何软件的了解和运用，动态几何的教学理念在数学课堂中并未得到广泛的运用，但绝大部分教师对这一理念有兴趣，想要在自己的课堂中进行尝试。本文基于这一现象，结合具体实例，对“动态几何”在培养学生空间观念的方法与价值方面进行阐述。

二、思考：“动态几何”的内涵特质

动态几何是在近现代数学思想的基础上发展起来的一种几何思想，它起源于20世纪80年代，最初的目的是利用相应的计算机软件代替圆规和直尺画直线、圆及其交点等几何图形。

著名数学家A.H.柯尔莫戈洛夫指出：“只要有可能，数学家总是尽力把他们正在研究的问题从几何上视觉化。”以信息技术为依托，动态几何为这种“几何可视化”增加了动态的元素。在众多的动态几何软件中，“几何画板”的作用不容小觑。点、线、圆是其基本元素，一方面几何画板可以进行平行线、垂线等的构造，能度量图形的周长、面积，同时它还具有多种图形变换功能，包括平移、旋转等;另一方面，画板中的某些对象可以用鼠标拖动或用参数的变化来直接驱动，而其他没有被拖动或直接驱动的对象会自动调整其位置，以保持图形原来设定的几何性质。它比PPT更能轻松解决“图形运动和变化”的问题，它打破了Flash动画只能按照设定的桥段走的局限性。它让图形与几何的学习变得直观、生动、丰富，对发展学生的空间观念、培养创新精神和实践能力有着十分重要的价值。本文着重描述“几何画板”在发展学生空间能力方面的实践。

三、追寻：“动态几何”的实践策略

动态几何贯穿于“图形与几何”的四大领域（图形的认识、测量、运动与位置）学习的全过程。通过观察、想象、比较、综合、抽象分析的过程，发展学生的空间观念。

（一）变“静”为“动”，发展空间知觉

数学知识是丰富多彩的，但呈现在教材中的知识是静态的、抽象的，如何把内隐的、压缩的过程直观化、外显化，动态几何的“动态演示”功能恰好能做到这一点。

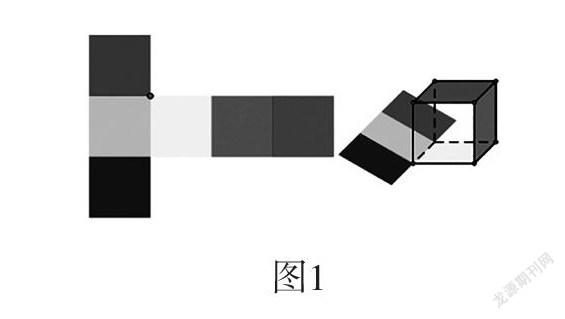
以“正方体展开图”为例。这是苏教版数学六年级上册的内容，是学生在认识正方体后的一节课程。教材编排这节课的目的是通过教学正方体的展开图来培养学生的空间观念。在平时的教学中，教师往往直接告知学生展开图的类型分别有“1-4-1”“2-3-1”“3-3”这三种模型，并将其对应的展开图以图片形式呈现。这样的教学过程，学生的空间思维并没有得到发展，更多的只是死记硬背。而动态几何就能很好地把这一过程清晰地演绎出来（如图1、图2）。

如图1，左侧是平面展开图，右侧是立体图，通过拖拽可以将正方体按照左侧展开图的形式一步一步展开;如图2，也可以将展开图还原成正方体。通过演示，让学生经历“立体—平面—立体”的思维过程，将静态的、抽象的知识动态化、外显化，学生的空间思维在一开一合之间得到了最大的发展。

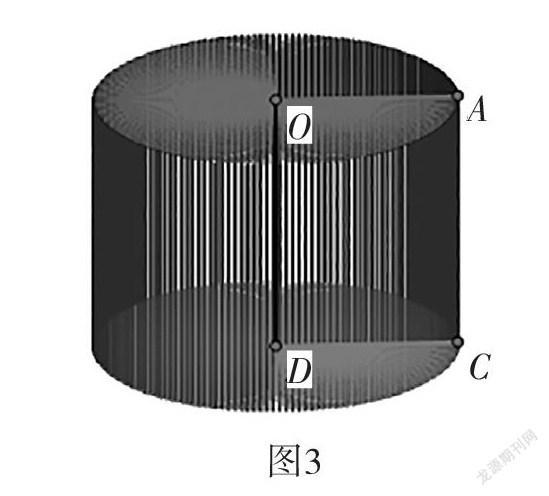
认识圆柱的时候，也可以引入动态几何。教师用几何画板，将一个点沿着直线运动，另一个点随意运动，在移动的过程中利用“追踪点”功能留下点的轨迹，学生发现点的运动轨迹可以是直线，也可以是曲线。接下来教师提问：想一想，線段的运动会形成怎样的图形呢？学生思考后继续观察几何画板中线段通过平移或旋转可以得到平面图形。此时，学生能联想到通过面的运动就可以得到立体图形。学生这样的猜想是否正确，教师可以让学生利用手中的长方形或圆形纸片自主操作，并讨论交流。最后，教师通过几何画板来验证：将长方形绕着线段OD旋转，保留长方形旋转一周的轨迹，形成圆柱（如图3）;或将圆O沿直线方向向下拉动，留下的轨迹也是圆柱（如图4）。

这一教学过程，由观察静态图片变为问题引领下的动态动画呈现，动态几何丰富了几何图形教学的方式，化抽象为直观，化单一表征为多元表征。通过教师的引导，学生在已有知识的基础上进行建构，空间知觉以“零维—一维—二维—三维”的方式得到发展，教师潜移默化地渗透了平面图形与立体图形间的联系，达到了知识间的内部迁移，深化了学生对“点动成线”“线动成面”“面动成体”的感知和理解。学生有了这样的表象依托后，教师可以进一步让学生对比不同素材旋转后所得到的圆柱的特点，从而深刻理解圆柱的粗细、高矮与什么有关，为接下来圆柱的表面积和体积的学习打下坚实的基础。

（二）变“散”为“连”，丰富空间表象

理论和实践告诉我们，小学生形成、发展空间观念主要依靠“视觉”和“触觉”，而实践操作是个体化的、散点状的，引进动态几何，在变与不变比较中，可以沟通图形之间的联系。

几何画板中的动画功能是最基本的一项功能，在制订路径（线段、直线、圆等）上构造一个点，这个点就可以在既定的轨迹上往正反两个方向运动。运动的方式可以用鼠标按住点来运动，也可以设置动画按钮来控制运动。下面就以两个具体实例来阐述：

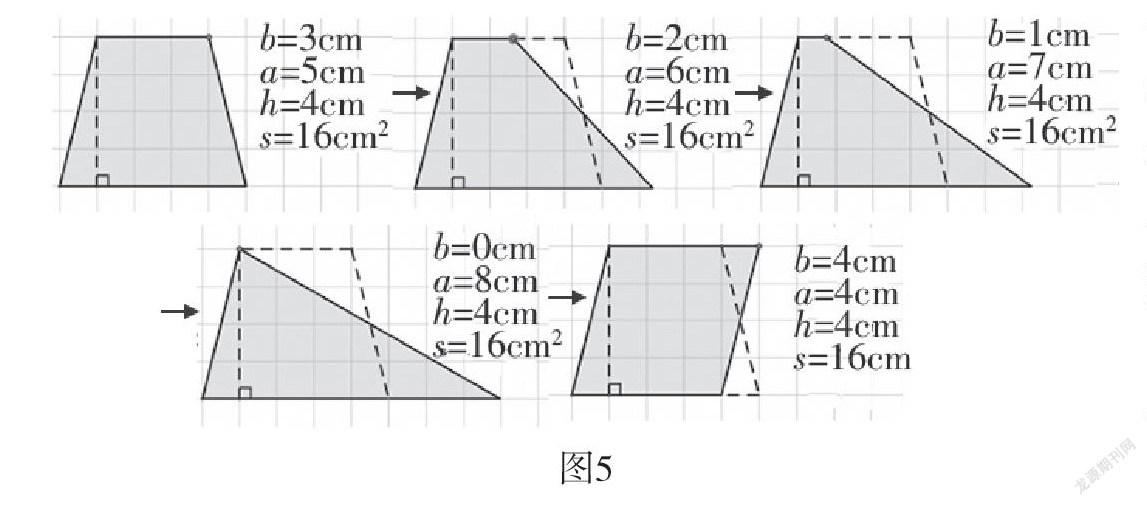
“多边形面积的整理与复习”一课中，要求学生“在方格图上画一个与梯形的高和面积都相等的图形”。教师在讲解过程中，可以利用几何画板点的动画功能，让梯形右上方的一点，沿着上底所在的直线这条轨迹运动，从而制作出动画（如图5）：

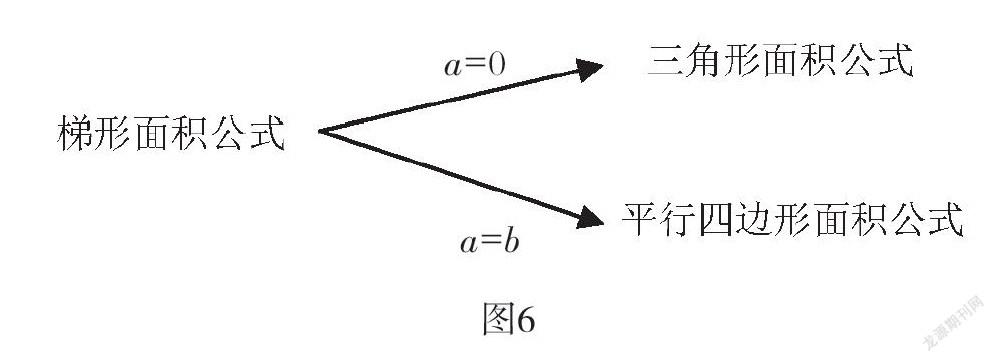
在这一开放性问题的引领下，学生自主探究，个性化表达，而在分享交流中，通过几何图形的动态演示，为学生直观感知图形间相互转化的运动过程创造可能，尽管图形的形状在变，但图形的面积没有发生改变，本质在于平行线之间的距离处处相等。正是基于这一前提，学生在这节课中，感受到了数学的统一之美：当梯形上底缩小为0时就成了三角形，当梯形上、下底相等时就成了平行四边形（如图6）。

（三）变“虚”为“实”，发展空间观念

抽象是数学的主要特征之一。基于小学生的认知特点，借助动态几何软件，可以给抽象的知识以直观的支撑，让空间观念真实可及。在探索“三角形三边关系”时，学生的操作体验是这节课中必不可少的环节。但上过这节课的教师都知道，三角形的三条边是线段，但教师准备的材料（塑料吸管、吸铁磁条等）在围成三角形时都会存在误差。在教学过程中，如何合理解释“两边之和等于第三边”这种不能构成三角形的情况，是在上这节课时的一个隐藏的却避无可避的“雷”。

利用几何画板就能把这个不易操作的实验过程以动态直观的形式真实呈现。

值得一提的是，几何画板中的动画功能和Flash是有区别的：Flash中的动画是既定的，教师一般根据教学设计提前制作，没有实时演示功能;而几何画板中的动画功能，教师可以通过右侧的控制按钮实现实时演示功能。这样做的好处是让课堂更具交互性，且通过两条边的顶点逐渐靠近，让学生感受到两边之和与第三条边相等是没有办法围成三角形的，也让学生感受到数学作为一门科学的严谨性。

数学结论的得出，经历的过程一般都是“分析—假设—实验—验证”这四个步骤，教师在教学过程中为了让学生感受数学这门学科的严谨性，都会告诉学生要进行多次实验，才能得出正确的结论。但这个“多次实验”往往既费时又费力。以“圆的面积”这节课为例，在推导圆面积公式的时候，教师通过将圆等分拼成类似长方形，从而推导得到圆面积的计算公式。

单纯地用剪拼的操作来推导显然太麻烦，而且效果也不理想，如果是一般的课件其预设又太单一（圆等分的份数只能事先预设，不能根据课堂生成随机改变）， “圆等分的份数越多，拼成的图形越像长方形”。对于这一点教师往往只能让学生发挥想象，而对空间观念比较薄弱的学生来说，这一过程并未在其大脑中建立表象，利用几何画板，就可以根据学生的回答将圆等分，把思维的过程可视化，真正做到了以“一图应万变”。

总之，动态几何是为了解决传统数学教学中难以解决的问题，是为了从根本上改变数学学习方式，有利于学生更好地理解与思考。教学中，一方面要坚持学生本位，要考虑学生的认知特点;另一方面要坚持学科本质，要考虑教学目标，让信息技术与小学数学相辅相成，在发展空间能力的同时，实现学生数学素养的提升。

【参考文献】

[1]毛雪琴，何姝珊.动态几何在中学数学教学中的应用及其价值[J].高等函授学报（自然科学版），2008（3）.

[2]张文梅.几何画板对初中学生几何动态问题解决的有效性探索[D].上海：华东师范大学，2010.

[3]庄振林.几何画板在高中解析几何教学中的应用研究[D].呼和浩特：内蒙古师范大学，2013.

[4]李春娟.浅谈小学生空间观念的培养[J].小学教学参考，2014（23）.

[5]包静娟.用本原性问题驱動数学理解[J].教育研究与评论（小学教育教学），2018（10）.