全椅式边含薁缺陷石墨烯纳米片的二阶非线性光学性质

郑雪莲，杨翠翠，田维全

（1.绵阳师范学院化学与化学工程学院,绵阳621000；2.重庆大学化学化工学院,理论与计算化学重庆市重点实验室,重庆401331）

自2004年实验成功分离出石墨烯以来［1］，具有独特性质的石墨烯一直是研究热点.然而，由于石墨烯具有零带隙，这极大地限制了石墨烯在晶体管等电子器件中的应用［2］.因此，人们发展了许多打开石墨烯带隙的方法，如制备双层石墨烯［3］、基底诱导调节带隙［4］、氢化石墨烯［5］和合成有限的石墨烯纳米片（GNSs）和石墨烯纳米带（GNRs）［6］.由于石墨烯边缘具有独特的电子、磁学性质和化学反应活性［7］，关于石墨烯边缘的研究近年来备受关注.其中，石墨烯非手性边缘已被观察到并占主导地位［8］.锯齿边存在占据非键（相邻碳原子价键未杂化p轨道基本保持未杂化时原子轨道形态）边缘态，容易发生反应，其稳定性低于椅式边［9，10］.具有不同形状的GNSs，如六边形GNSs（HGNSs）、三角形GNSs（TGNSs）和平行四边形GNSs（PGNSs）等，能产生新颖的电子、光学和磁学性质［11，12］.这些GNSs的边缘类型（即锯齿边或椅式边）对其电子性质有很大的影响［13，14］，它们不仅具有良好的π共轭电子结构，保持了碳基纳米材料较强的热稳定性和化学稳定性，而且由于量子限域效应产生了很多独特的性质.这些GNSs的非线性光学（NLO）性质也得到了研究，但由于原生HGNSs，TGNSs和PGNSs等是非极性或弱极性的，因此以前的研究主要集中于这些GNSs的三阶NLO性质［15~17］，对其二阶NLO性质研究较少.

石墨烯在加工过程中由于动力学因素易产生一些本征缺陷，如Stone-Wales缺陷（2a）［图1（A）］［18］是石墨烯体系中拓扑无序的最简单例子.空位缺陷会导致形成其它类型的缺陷石墨烯纳米片［19，20］［图1（B）~（D）］，其中5-8-5缺陷的稳定性较差［21］.由于薁缺陷具有极性［22］，薁缺陷的引入可以使原生碳基纳米材料具有一定的极性，进而赋予或改善其二阶NLO性质［23］.目前，对于具有薁缺陷的不同形状GNSs的NLO性质（特别是二阶NLO性质）的研究较少，并且薁缺陷的数量与纳米片形状对薁缺陷GNSs的NLO性质的影响机制还不明确.因此，本文以化学稳定性较好的全椅式边HGNSs，TGNSs和PGNSs为初始模型，保持边缘形状（全椅式边）不变，分别引入2a，3a和4a本征缺陷（图1），研究了这些GNSs的电子结构和二阶NLO性质与薁缺陷数量和纳米片形状的相关性.

Fig.1 Structures of GNSs with 2a(A),5⁃8⁃5(B),3a(C)and 4a(D)defects

1 结构模型和计算方法

对全椅式边石墨烯纳米片（AGNSs）的结构进行优化（图2）.六边形、三角形和平行四边形的原生AGNSs分别表示为AH，AT和AP.实验已合成了一些类似的不同形状的AGNSs［24~26］.本文使用基于Kohn-Sham模型的密度泛函理论的PBE0［27］方法和6-31G（d，p）基组［28，29］，运用Gaussian 09程序［30］对研究体系进行几何结构优化，所有结构的驻点性质均通过振动频率分析进行了验证.为了比较，用同样的方法对六边形、三角形和平行四边形的全锯齿边石墨烯纳米片（ZGNSs，ZH，ZT和ZP）进行了优化（图S1，见本文支持信息）.在AH，AT和AP中分别引入2个（2a）、3个（3a）和4个（4a）薁缺陷［图1（A），（C）和（D）］，得到了相应的薁缺陷AGNSs（AH-2a~4a，AT-2a~4a和AP-2a~4a）.采用ZINDO［31］基于Franck-Condon原理模拟了这些体系的电子光谱，在ZINDO/CIS计算中包括了体系中所有的π分子轨道.基于ZINDO预测的激发能、偶极矩和跃迁偶极矩，利用LinSOSProNLO软件［32，33］，结合态求和（SOS）模型［34，35］预测了体系的二阶NLO性质.已有研究证实ZINDO/SOS方法对碳基材料的电子光谱和NLO性质的预测具有良好的可靠性和对大体系的模拟高效性［36，37］.根据SOS模型［34，35］，分子的第一超极化率张量βijk（a.u.）可表示为

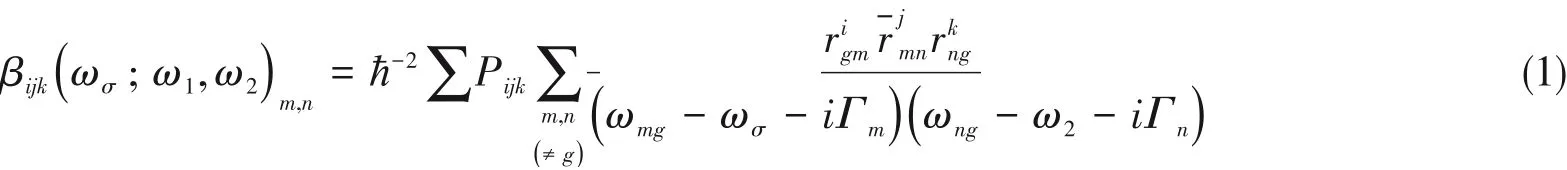
式中：ħ为狄拉克常数（h/2π）；ωσ=∑ωi（i=1，2），其中ωi为外场频率，表示从基态g到激发态m的跃迁矩为偶极波动；Γm=0.08×εm/ε2［38］为激发态m的逆辐射寿命（阻尼系数），其中εm（=ħωmg）是基态到第m个态的激发能，ε2是第2个态（也是最低的）的激发能；∑P表示通过置换跃迁矩（或偶极波动）和外场对的所有项的求和.

β的取向平均<β>由下式［39］计算：

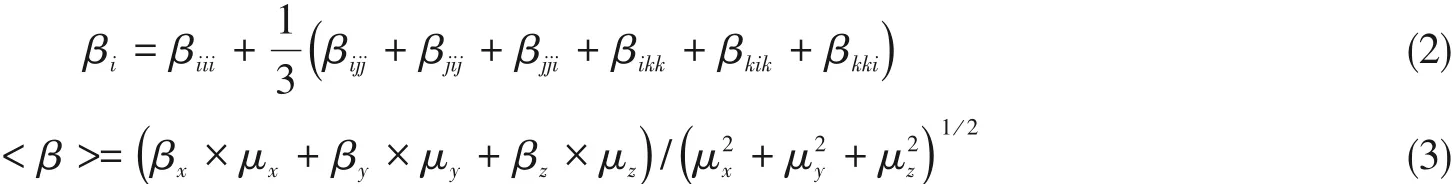
式中：μi（C∙m）为i方向的偶极矩.

2 结果与讨论

2.1 几何和电子结构

所有研究体系的优化构型见图2和图S1，原生的全锯齿边和全椅式边GNSs均具有平面结构.相比于具有较高对称性的原生GNSs，薁缺陷的引入使GNSs的对称性降低，除了AH-2a和AT-2a具有Cs对称性以外，其它的薁缺陷GNSs的对称性均为C1.采用Multiwfn 3.6［40］计算的AGNSs的分子高度r（图2）表明，薁缺陷引入后所有AGNSs均发生了不同程度的形变.

表1列出了所有GNSs的电子性质.除了AH-3a，ZT，AT-3a和ZP之外，其它GNSs的基态均为闭壳层单重态.其中ZT和ZP的能隙最小，均约为0.43 eV（表1），这是由于锯齿边会出现不稳定的占据非键前线轨道［图S2，见本文支持信息，ZT和ZP的最高占据分子轨道（HOMO）中出现明显的非键特征］，使体系具有较低的能隙.而AH，AT和AP的HOMO均为π成键轨道.值得注意的是，ZH的能隙为2.31 eV，具有较好的电子动力学稳定性（即电子需要吸收更多的能量跃迁到空轨道），并且其HOMO中没有出现非键特征，这可能是由于在六边形的6条边上均只有两个连续的锯齿状CH，不足以形成非键轨道［41，42］.Philpott等［43］发现，当六边形ZGNSs的每条边上相连的苯环数目≥9时，纳米片的基态会从闭壳层单重态变为双自由基单重态.

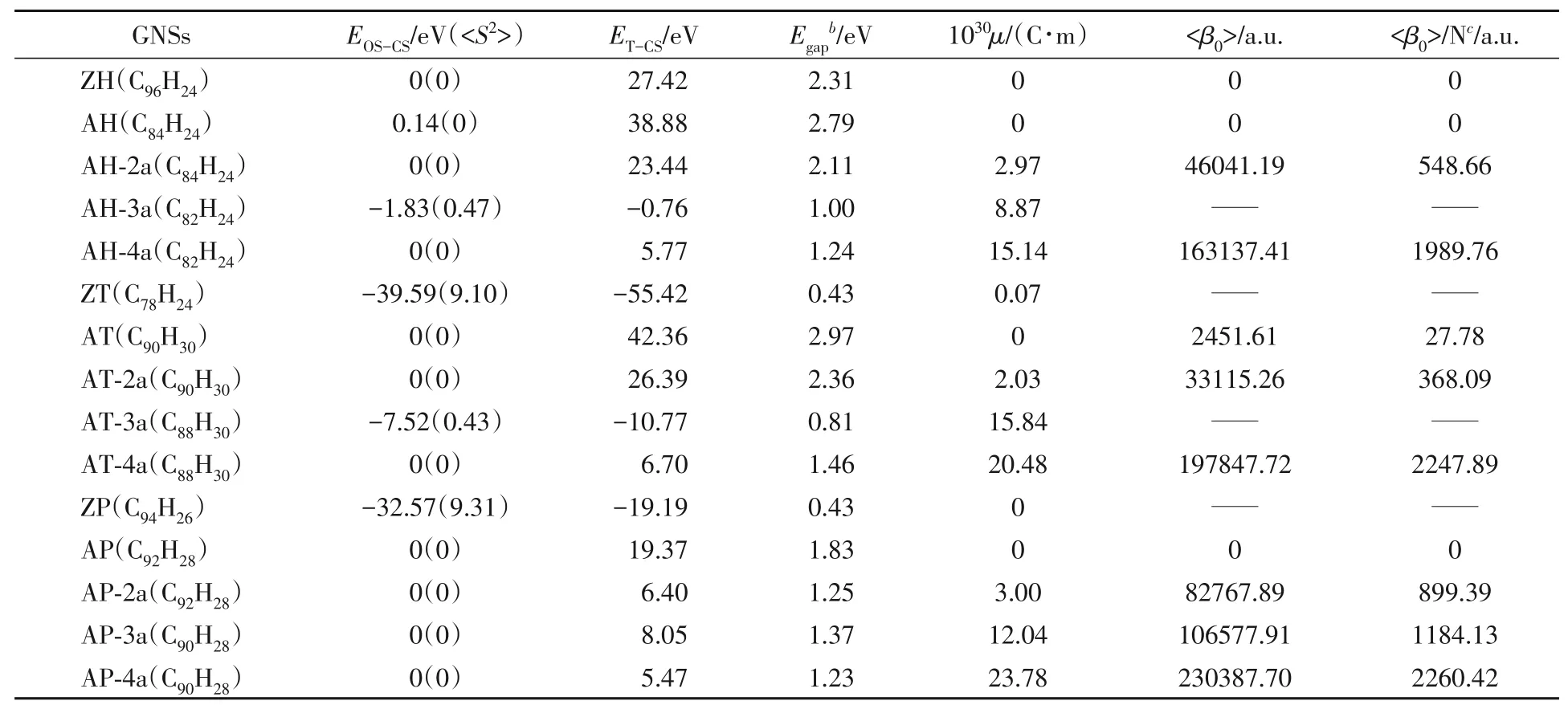
Table 1 Electronic properties and static first hyperpolarizability(<β0>)of closed-shell singlet GNSs predicted using PBE0/6-31G(d,p),ZINDO and SOS model a

所有原生AGNSs均具有弱（或非）极性.引入薁缺陷后，随着缺陷数量的增加，薁缺陷AGNSs的偶极矩也增大.在所有薁缺陷AGNSs中，AP-4a具有最大的偶极矩（23.78×10−30C∙m）.所有AGNSs的分子静电势表面图（MEPS）也反映了此现象（图S3，见本文支持信息）.在所有原生AGNSs的MEPS中，电子均匀分布在整个纳米片上.薁缺陷的引入使正、负电荷中心发生分离，缺陷数量越大，分离程度越明显，即极性越大.

2.2 静态第一超极化率

Karamanis等［44］通过控制BN片段的形状、大小和覆盖面积来调节GNSs的二阶NLO响应中偶极和八极的相对贡献，使BN掺杂的GNSs产生了优异的二阶NLO性质.在该研究的启发下，本文将由薁单元组成的不同大小的片段引入化学稳定性好且形状不同的原生AGNSs中，使其发生电荷分布极化，进而产生强的二阶NLO响应.表1列出了这些闭壳层单重态的AGNSs的<β0>.在3个系列（HGNSs，TGNSs和PGNSs）中，<β0>的变化有一致的规律，即随着薁缺陷数量的增加，<β0>增大，其中AH-4a，AT-4a和AP-4a在各自系列结构中有最大的<β0>.图3给出了各系列中含有4个薁缺陷的AGNSs的<β0>随电子激发的演变，其它薁缺陷AGNSs的<β0>随电子激发的演变如图S4（见本文支持信息）所示.

AH-4a，AT-4a和AP-4a的<β0>均随电子激发逐渐增加，并在外场约为6.00 eV处趋于收敛（图3）.AH-4a的<β0>为163137.41 a.u.，平均每个重原子的<β0>（<β0>/N：N为分子的碳原子数）为1989.76 a.u.（表1）.在最低偶极允许电子激发0.95 eV（1309.1 nm）处的HOMO到LUMO的电荷转移电子激发（所涉及的占据分子轨道和未占据分子轨道分布在不同区域）对AH-4a的<β0>有最大的贡献，为44210.01 a.u.［图3（A），图S4和表S1，见本文支持信息］.另一个有较大贡献（31367.42 a.u.）的电子激发发生在2.09 eV（594.3 nm）处.所涉及的电子激发是电荷转移激发和主要发生在4个薁缺陷上的垂直电子激发（所涉及的占据分子轨道和未占据分子轨道分布于同一区域）的混合.AT-4a的<β0>为197847.72 a.u.，平均每个重原子的<β0>为2247.89 a.u.（表1）.在1.56 eV（793.9 nm）处集中在4个薁缺陷上的垂直电子激发［图3（B），图S4和表S1］对AT-4a的<β0>有最大的贡献，为42487.63 a.u.，另外两个在2.85 eV（435.3 nm）和3.14 eV（394.4 nm）处的电子激发也有重要贡献，<β0>分别为26627.40和30790.97 a.u.，是HOMO−1~HOMO−8到LUMO的电荷转移电子激发.在所有研究的AGNSs中，AP-4a具有最大的<β0>，为230387.70 a.u.，平均每个重原子的<β0>为2260.42 a.u.（表1）.在1.70 eV（727.8 nm）和2.08 eV（596.6 nm）处明显的电荷转移电子激发对<β0>有较大的贡献，分别为48224.26和28648.42 a.u.［图3（C），图S4和表S1］.1.29 eV（961.8 nm）和2.15 eV（577.3 nm）处的电子激发对<β0>也有明显的贡献，分别为17058.25和16249.15 a.u..图4（A）~（C）分别描述了对AH-4a，AT-4a和AP-4a的<β0>有主要贡献的电子激发的电子-空穴分布图［40，45］.指数D（nm）是指空穴的质心和电子的质心之间的距离（即用来量化与电子激发相关的电荷转移距离）.电子-空穴分布图显示的结果与前面分析的主要电子激发的跃迁性质有较好的一致性.

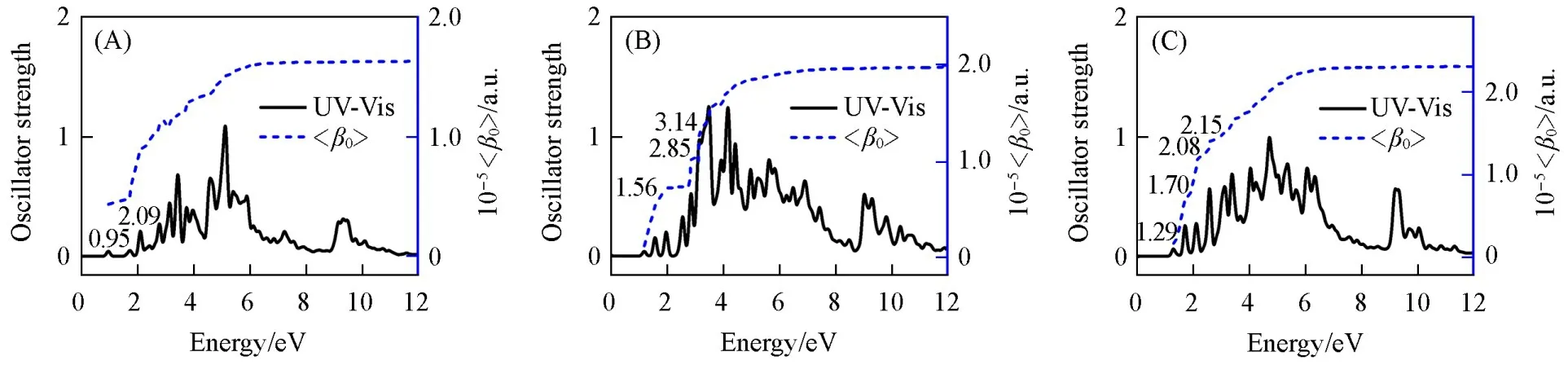
Fig.3 Evolution of the<β0>with electron excitations of AH⁃4a(A),AT⁃4a(B)and AP⁃4a(C)

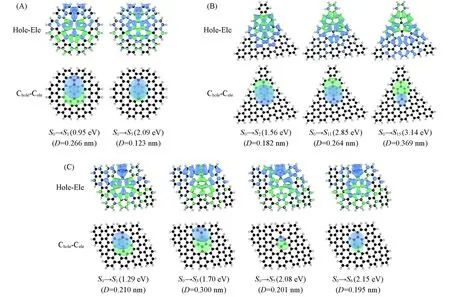
Fig.4 Real space representation(isovalue=0.0006 a.u.)of electron and hole distribution of electron excitations with dominant contribution to<β0>of AH⁃4a(A),AT⁃4a(B)and AP⁃4a(C)

在所研究的AGNSs中，随着薁缺陷数量的增加，<β0>显著增大.另外，纳米片形状对AGNSs的<β0>也有不可忽略的影响.当纳米片中的薁缺陷数量一致时，PGNSs的<β0>始终大于HGNSs和TGNSs的<β0>（表1）.从这些薁缺陷GNSs中参与主要电子激发的分子轨道可见，对<β0>有最主要贡献的电子激发涉及的分子轨道分布主要集中在薁缺陷所组成的薁功能片段上.说明相互连接着的薁单元形成了一个整体的薁功能中心，这个功能中心影响了AGNSs的电子结构，使其发生不同程度的电荷分布极化，进而改善了AGNSs的二阶NLO性质.相较于AH-4a和AT-4a，AP-4a中对<β0>起最主要贡献的电子激发是明显的电荷转移跃迁，这可能也是AP-4a具有较大的<β0>的原因.另外，基于式（1）详细分析了AH-4a，AT-4a和AP-4a中对<β0>有较大贡献的电子激发的本质.表S2（见本文支持信息）结果表明，这些薁缺陷AGNSs均有较大的基态偶极矩和偶极波动，进而使其具有大的<β0>.AP-4a中还具有较大的跃迁偶极矩，使AP-4a的<β0>大于AH-4a和AT-4a的<β0>，与前面提到的AP-4a中有明显的电荷转移电子激发相符.

2.3 二维二阶非线性光谱

二维二阶非线性光谱［46~48］包含体系在外场下的所有二阶NLO响应.实验上很难得到分子（或体材料）在很大的外场范围内的二阶NLO响应，特别是很难得到和频产生（SFG）和差频产生（DFG）.图5展示了AH-4a，AT-4a和AP-4a在0~6.00 eV外场范围内，扫描步长为0.05 eV的二维二阶非线性光谱.

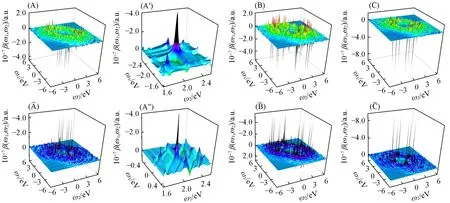
Fig.5 Two⁃dimensional second order NLO spectra of AH⁃4a(A),AT⁃4a(B)AP⁃4a(C)scanned up to 6.00 eV with scanning step size of 0.05 eV

由图5（A）可以看到，在AH-4a中，强的单光子共振发生在ω=0.95 eV处.在（0 eV，0.95 eV）处的响应为强的电光Pockels效应（EOPE），在（0.95 eV，−0.95 eV）处的响应为强的光学整流（OR），与0.95 eV（1309.1 nm）处的电子激发发生共振.步长为0.005 eV的精细扫描发现在外场为2.085 eV处有强的EOPE（−2.085 eV；2.085 eV，0 eV）和OR（0 eV；2.085 eV，−2.085 eV）［图5（A′）和5（A″）］.另外，在（3.45 eV，−1.35 eV）和（3.45 eV，−2.10 eV）处有较强的DFG.由图5（B）可见，在AT-4a中，强的单光子共振发生在ω=2.85，3.15和3.50 eV处.最强的EOPE（−3.15 eV；3.15 eV，0 eV）和OR（0 eV；3.15 eV，−3.15 eV）可能会与3.14 eV（394.4 nm）处的电子激发发生共振.在（3.15 eV，−0.30 eV）和（3.15 eV，−2.85 eV）处有强的DFG.在（1.30 eV，1.55 eV）和（1.55 eV，1.30 eV）处存在强的SFG（ω1+ω2=2.85 eV）（ω1，ω2∈［0 eV，2.85 eV］）.由图5（C）可见，在AP-4a中，强的单光子共振发生在ω=1.70和2.15 eV处.在（0 eV，1.70 eV）处的响应为强的EOPE，在（1.70 eV，−1.70 eV）处的响应为强的OR，与1.70 eV（727.8 nm）处的电子激发发生共振.在（2.55 eV，−0.45 eV）和（2.55 eV，−2.10 eV）处有强的DFG.综上所述，AT-4a和AP-4a中强的EOPE和OR等特殊响应过程都发生在可见光区，而 AH-4a中的这些特殊响应过程都出现在近红外区.此外，AH-4a和AP-4a中有强的DFG，而AT-4a中不仅有强的DFG，还有强的SFG，这些预测结果都能为该类AGNSs的光电实验研究和应用提供有用的理论参考.

3 结 论

保持GNSs的边缘均为椅式边，使用密度泛函理论方法和ZINDO/SOS方法研究了不同纳米片形状和薁缺陷数量的AGNSs的电子结构和二阶NLO性质.非键边缘态的存在使ZGNSs可能具有多组态特征，化学稳定性较差.而AGNSs的化学稳定性较好，极性薁缺陷的引入诱导了AGNSs的电荷分布极化，研究的多数薁缺陷AGNSs在保持良好化学稳定性的同时，具有显著增强的二阶NLO响应.薁缺陷AGNSs大的二阶NLO响应不仅取决于薁缺陷的数量（占主导作用），还与AGNSs的形状有关，其中平行四边形的AGNSs—AP-4a的<β0>最大.薁缺陷组成的片段作为功能中心，除了极化AGNSs电荷分布外，还参与对二阶NLO响应有主要贡献的电子激发.此外，薁功能片段周围的苯环也有不可忽视的作用，参与苯环和薁功能片段之间的电荷转移电子激发.本文在设计具有优异二阶NLO性质的GNSs时，将薁缺陷数量和纳米片形状影响因素都考虑进去，找到了具有二阶NLO性质最优的结构，为实验合成相应的全碳NLO材料提供了理论参考信息.此外，薁缺陷的排列方式和薁缺陷组成的功能片段分布在GNSs中的不同位置（如中心或边缘）都对GNSs的电子结构有影响，进而可能影响其二阶NLO性质.本文研究结果可为未来的碳基非线性光学材料的设计提供实用的策略和有用的信息.

支持信息见http：//www.cjcu.jlu.edu.cn/CN/10.7503/20210806.