LiCl-NaCl-KCl-H 2O溶液体系渗透压的分子动力学模拟
2022-05-25陈瀚翔边绍菊
陈瀚翔,边绍菊,胡 斌,李 武
(1.中国科学院青海盐湖研究所,中国科学院盐湖资源综合高效利用重点实验室,西宁810008;2.青海省盐湖资源化学重点实验室,西宁810008;3.中国科学院大学,北京100049)
水盐混合溶液在自然环境、无机盐工业中极为常见[1~3].溶液中普遍存在的离子-离子和离子-水相互作用对其热力学性质,特别是超额性质有极大影响.然而,分子、原子层面的相互作用和宏观的热力学性质之间的关系在大多数时候非常模糊[4~6].基于唯象理论建立的传统溶液模型往往需要针对特定体系引入大量相关参数,用以描述复杂的相互作用对热力学性质的影响[7,8].然而,这些方法在确保精度的同时也带来了高昂的建模成本和较差的通用性[9~11].与此同时,分子动力学中如极化力场、新型建模方式等新技术的开发,为其深入研究电解质溶液的内在机制提供了新的可能性[12~16].大量研究证明,通过对溶液微观和介观层面的研究,同样可以对一系列热力学性质进行计算和预测[17~21].并且,由于分子动力学建立在基本的牛顿运动方程、系综理论和通用的参数之上,相对于形式和参数复杂的传统溶液模型具有更好的通用性和扩展性.
分子动力学结合水溶液渗透压模拟(OPAS)技术,通过设计一组虚拟半透膜与体系中特定的粒子交互,能够更加精确地还原渗透压形成的过程[22~26].并且可同时提供粒子在有膜存在的情况下的分布等信息,对于研究混合溶液体系的渗透性质非常适用.目前,已利用该方法研究了简单混合物体系的热力学性质,如研究Lennard-Jones势作用的理想混合物模型、NaCl溶液、甲醇-水和Ar-O2的渗透压、活度等性质[22,23,25],并且取得了较好的结果.但尚未见使用该方法对三元以上的混合物的研究报道.
针对盐湖卤水渗透压的预测问题,本文选取了LiCl-NaCl-KCl-H2O体系作为研究对象.该体系是盐湖卤水的一个基本子体系,并且3种盐同属于碱金属氯化物,具有相似的化学性质,更能在研究中考察方法的通用性.采用OPAS分子动力学模拟方法,通过分析和处理模拟中产生的分子轨迹以及膜与离子作用力和作用能,从而计算溶液的渗透压(P).对不同组成、不同浓度的溶液体系进行标准化、批量化的模拟计算,并与实验数据和Pitzer模型计算值作对比,以考察方法的精度和通用性,探究了影响模拟精度的关键因素,总结了该方法在研究混合盐溶液体系热力学性质时的优势和劣势.
1 实验部分
1.1 模型构建
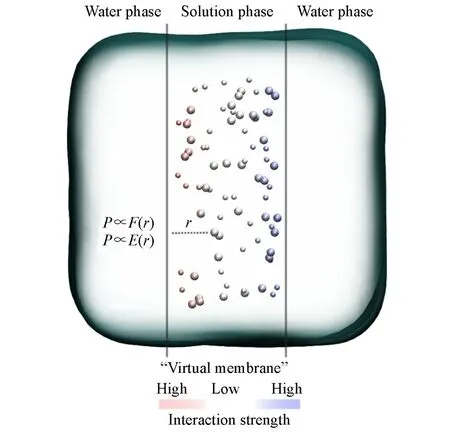
Fig.1 Illustration of the simulation model
在周期性长方体模拟盒子中,指定两个平行于yz平面的面为虚拟半透膜.膜的x轴坐标分别为xm,1=0.25Lx+xmin和xm,2=0.75Lx+xmin(其中,Lx和xmin分别表示x轴的总长和下界).同一个重复周期内两个膜之间的空间称为膜内空间,其余部分称为膜外空间.初始构型中,膜内空间填充以待考察的溶液,膜外空间填充纯水.建模示意图如图1所示,图中蓝色背景表示水分子,球体表示离子,实线表示虚拟半透膜的位置.模拟过程中,体系的构型基本保持不变.特别需要指出,等温等压系综(NPT)模拟中,盒子的尺寸因为压力而变化的同时,虚拟半透膜的位置同时更新,即xm,1和xm,2的坐标跟随Lx和xmin变化,但相对位置总处于x轴总长的0.25和0.75倍处.膜内空间的体积也随上下界位置发生变化,但其相对体积始终占据总体积的一半.
虚拟半透膜本质上是一组建立在yz平面上的力场函数,与离子发生相互作用,使离子被束缚在膜内空间,形成溶液相.但膜不与水分子发生交互,允许其自由通过,即力场函数的作用范围不包括水分子.

虚拟半透膜的力场按照Lennard-Jones势的形式[27~29]建立如下:式中:Ei(kJ/mol)和Fi(kJ·mol−1·nm−1)分别为膜对离子i的作用能和作用力;ri(nm)为离子到膜的垂直距离;ϵm(kJ/mol)和σm(nm)为膜的Lennard-Jones参数.对于各种膜-离子的相互作用,采用Lorentz-Berthelot混合规则[30,31]生成对应参数,整体而言与实体膜(如有机高分子聚合物)的处理方式相似.
对膜的Lennard-Jones参数采取正交实验优化,选取4.4 mol/kg NaCl溶液为对象,正交实验的实施方式与后续成品模拟的方式一致,考察模拟的最终阶段的溶液相密度和模拟的稳定性,并根据文献值计算密度的相对误差.所考察的两个参数中,ϵm选取0.1046,
0.2092,0.4184,0.8368,1.6736,3.3472 kJ/mol 6个水平,σm选取0.025,0.05,0.1,0.2,0.4,0.8 nm 6个水平.实验结果表明,以ϵm=0.4184 kJ/mol搭配σm=0.1 nm的参数组合可产生最小的溶液相密度误差.图2以填色图方式表示各组参数溶液相密度的相对误差,其中空白部分表示该组参数不能进行稳定的模拟.
在Kohns等[22]和Luo等[25]的研究中,采用半谐振势即Fi=cri形式的力场,将穿越到膜外的离子拉回膜内空间,这与本文使用的力场存在一定区别:虽然二者都是对远离膜内空间中心更远的离子施加更多的力,但半谐振势只有单向的作用,对于已经在膜内空间的离子缺乏一定的考虑,且文献[25]选取的半谐振势参数c=41.84 kJ/mol的根据也不明确.本文采用Lennard-Jones势的原因还包括:在模拟有实体膜(如CHON元素)组成的高分子聚合物存在的溶液时,该高分子同离子间的作用通常也采用Lennard-Jones势和静电相互作用来描述,而静电相互作用部分由于膜的净电荷约为0,其总和远小于Lennard-Jones势,因此本文采用的方式是合理的.
模拟中离子采用Joung-Cheatham力场[27,28,32],该力场专门基于近饱和溶液和晶体溶解度问题进行开发,在高浓度水盐混合溶液的溶解度[33]、活度[34]、化学势[35]等问题中相比于其它数种力场取得了更好的结果.并且,Joung-Cheatham力场支持大部分碱金属,碱土金属和卤族元素.考虑到天然的卤水和海水中还含有Ca,Mg,F等元素,采用该力场为以后的工作预留了一定的扩展性.
对于水分子,采用TIP3PEW模型[36~40]描述.在多种常用于极性水溶液的水分子模型(TIP3P,TIP3PEW,TIP4P,TIP4PPPPM,SPC/E)中,TIP3PEW模型更适合本体系.对4.4 mol/kg的NaCl-H2O溶液的体相进行模拟时,各模型溶液相密度和纯水相密度与实验值[41]的相对误差分别为−2.6%,−0.3%,−2.8%,1.2%和2.4%.
构建初始构型时,使用Packmol软件[42]利用随机算法将膜内空间对应的位置填充以约1.0 g/mL的待考察溶液,将膜外空间对应的位置填充以1.0 g/mL的水.
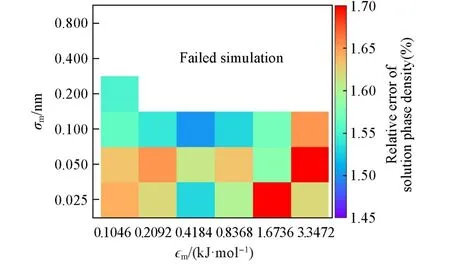
Fig.2 Relative errors of solution phase density of simulations using different membrane parameter sets
1.2 溶液体系的选择
对不同组成的LiCl-NaCl-KCl-H2O溶液及其3个三元子体系、3个二元子体系进行研究,三元子体系包括LiCl-NaCl-H2O,LiCl-KCl-H2O,NaCl-KCl-H2O;二元子体系包括LiCl-H2O,NaCl-H2O,KCl-H2O.其中,三元子体系中的两种盐的摩尔比(r)选取1∶4,2∶3,3∶2,4∶1.相当于其中一种盐占总摩尔浓度的20%,40%,60%,80%4种情况;四元体系的3种盐的r以n(Li)∶n(Na)∶n(K)表示,选取2∶1∶1,1∶2∶1,1∶1∶2.选取溶液体系组成的依据在于:(1)便于对照参考文献的实验值和模型值;(2)在无机盐工业中,需要处理的各种水盐混合溶液的浓度范围广,组成比例多变,要求方法和模型具有很好的通用性.
表1列出了初始选择的溶液体系的模型数量、对应的质量摩尔浓度和分子模型中粒子的数目.由于模拟中溶液相和纯水相的水分子可以自由交换,最终溶液的质量摩尔浓度是模拟过程中溶液相的质量摩尔浓度的时间平均值.
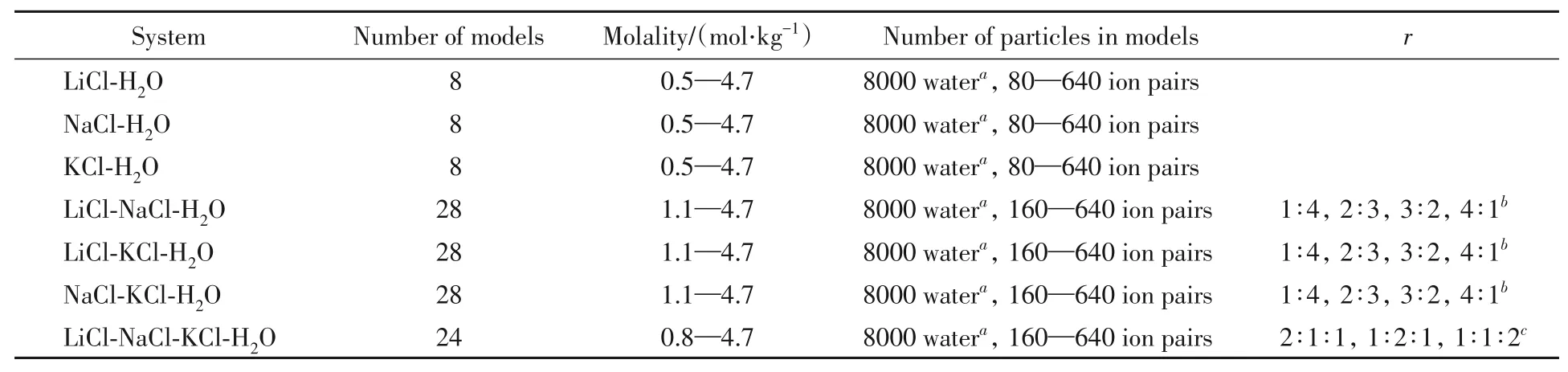
Table 1 Number of models,molalities and number of particles in models of all solution systems for simulation
1.3 分子动力学模拟
1.3.1 溶液体系渗透平衡模拟 利用LAMMPS软件[43]对各溶液体系进行分子动力学模拟,并收集模拟过程中的膜与离子间作用力和作用能,以及各粒子运动轨迹等信息.
初始模型准备完成后,对其进行能量最小化和预平衡.利用共轭梯度法对体系进行最高2000步的能量最小化,力收敛限设为4.184×10−5kJ·mol−1·nm−1,能量收敛限设为总能的10−4倍.对体系进行1 ns的正则系综(NVT)模拟作为预平衡,时间积分步长为2 fs,共5×105步.采用Nose-Hoover恒温算法控制温度,温度为298.15 K,耦合常数为200 fs.
体系预平衡后,进行5 ns的NPT模拟,时间积分步长为2 fs,共2.5×106步.采用Nose-Hoover恒温、恒压算法控制温度和压力,温度为298.15 K,耦合常数为200 fs;压力为1×105Pa,耦合常数为200 fs.模拟中仅允许盒子的体积沿x轴变化,由于膜平行于yz平面,其面积不变.每2 ps收集一次体系中膜与离子间相互作用力和作用能,以及温度、压力、密度等基本数据.以体系的密度作为判据确定体系是否已达到平衡,结果表明,所有溶液体系密度均在0.5~1.0 ns时间段内收敛至实验值附近;在处理数据和计算渗透压时,前2 ns视为对体系的压缩和平衡,只取后3 ns的数据作为计算的依据.
1.3.2 渗透压计算 使用两种方案计算体系的渗透压:(1)统计膜与离子间每个数据点相互作用力,并除以膜面积得到瞬时压强,再对瞬时压强作时间平均得到渗透压,简称力统计(FS)方法,如式(4)所示;(2)先对膜与离子间相互作用能进行统计和时间平均,以二元体系的数据作为训练集,利用多项式函数拟合相互作用能和实验渗透压,得到一组二元体系的多项式参数;以三元及四元体系的数据作为测试集,将对应二元体系的多项式参数按多元体系的离子摩尔比r混合,得到多元体系多项式参数,用于计算渗透压并进行验证,简称膜能量拟合(MEF)方法,如式(3)和式(5)~式(7)所示.

二元体系:

三元及四元体系:

式中:E(kJ/mol)和F(kJ·mol−1·nm−1)分别表示膜对离子施加的总作用能和总作用力;A(nm2)为膜面积;Ly(nm)和Lz(nm)分别表示体系y轴和z轴的长;P(MPa)表示溶液的渗透压;常数cn,c0,c1,c2表示MEF方法的多项式参数;mi(mol/kg)为多元溶液体系中i种溶液的质量摩尔浓度.
1.4 数据对比
将模拟得到的渗透压与实验数据[41,44~47]以及Pitzer模型和Dinane-Pitzer模型计算值作对比.其中,在反映各溶液体系渗透压随组成变化的图示中,实验数据以连续的折线表示;对于特定组成的单个数据点,由于NPT系综模拟本身的性质,模拟体系最终的温度和总浓度不可能与实验值完全相同,对比参考与实验值来自相同文献的Pitzer模型[41,45~47]和Dinane-Pitzer模型[44],取其计算值作为对比.Pitzer模型和Dinane-Pitzer模型都是直接基于实验值拟合的数学模型,在所研究的体系中,具有很好的准确度,可作为合适的参考对象.所有数据计算和对比完成后进行误差分析.
2 结果与讨论
2.1 二元体系的渗透压计算和MEF方法处理
对3个二元体系进行模拟的数值结果如表2所示.表2中膜能量、FS方法计算的渗透压、MEF方法计算的渗透压分别根据式(3)、式(4)和式(5)进行计算.并将两种方法计算的渗透压与文献[41]的参考值作对比.
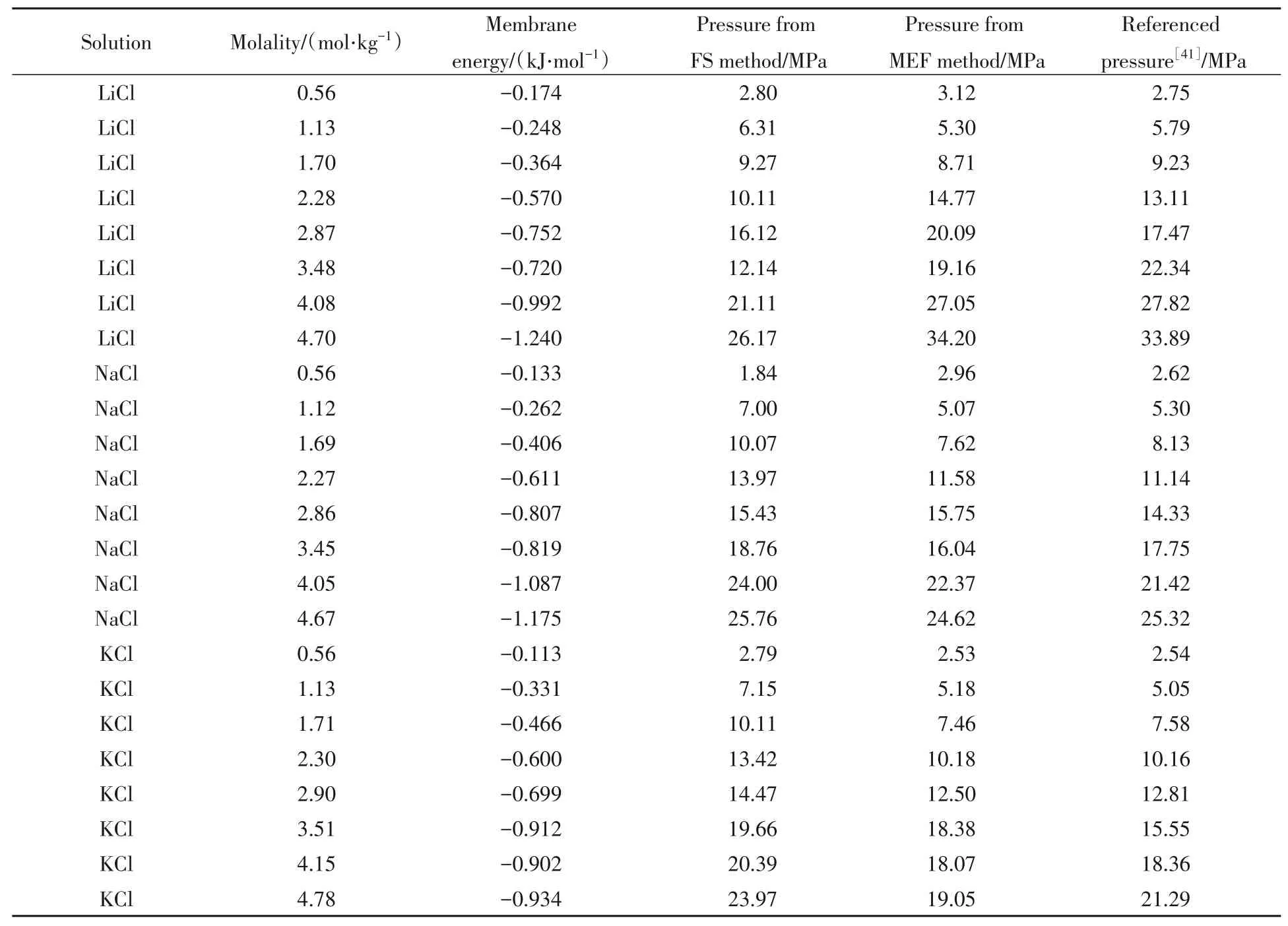
Table 2 Main numeric results of binary solution system simulations
其中,两种渗透压的计算方法都能够反映渗透压的变化趋势.以均方根误差(RMSE)计算,MEF方法的相对误差为1.8%,优于FS方法的4.6%.
图3(A)~(C)以折线图形式分别展示了3个二元溶液体系的渗透压计算值和参考值.对于LiCl溶液,FS方法在较高浓度时均表现出低于实验参考值的预测结果,而对于NaCl和KCl则给出略偏高的预测结果,且KCl偏高的程度高于NaCl.此外,在LiCl的预测结果中,浓度为3~4 mol/kg之间出现了一次非常明显的精度下降,使3.5 mol/kg时的渗透压计算值小于2.8 mol/kg时的值.对LiCl较高浓度的模拟轨迹进行分析,未发现有聚集、结晶等明显影响粒子分布的现象.
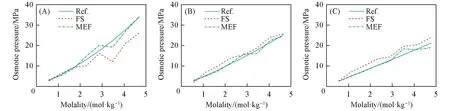
Fig.3 Simulated and experimental osmotic pressure of the binary systems of LiCl⁃H 2O(A),NaCl⁃H 2O(B)and KCl⁃H 2O(C)
考虑FS方法对渗透压的计算方式[式(4)],FS方法计算得到的渗透压准确度直接依赖于力场对膜-离子间Lennard-Jones相互作用力的准确度.而这类相互作用力准确度取决于两个方面,一方面是本文经过正交实验得到的膜相关参数,另一方面是离子本身的力场参数.前者,由于基于计算膜-离子总相互作用能的MEF方法,在各组成中都表现出更好的渗透压预测精度,并且在正交实验中,各组膜参数都能较好地还原溶液相的密度.因此,由于膜的建模方法和相关参数的不合适而造成FS方法准确度不佳的可能性较小.后者,考虑到包括本文所采用的Joung-Cheatham力场在内的十余种常用的电解质溶液力场都主要以溶液结构、水合能、溶解度等问题为出发点;且目前并无专注电解质溶液热力学超额性质的离子力场.因此,FS方法准确度不佳的主要原因来自于离子本身的力场参数并非完全适合于本文涉及的体系和渗透压问题的可能性较大.
将3个二元溶液体系的膜能量数据作为数据源,用来拟合MEF方法的多项式参数[式(3)],所得的一组拟合参数如表3所示,采用该组参数进行MEF方法计算的结果已在表2列出.

Table 3 Final fitted parameters of MEF method
对于三元和四元体系的MEF方法计算,仍然采用以上参数,按式(4)和式(5)进行依据膜能量对渗透压的计算.
2.2 三元体系和四元体系渗透压的计算
计算仍然采用相同的计算流程和模拟设置.三元体系的组成选取方面,以离子摩尔比r=n(cation,1)/n(cation,2)表示两种阳离子的浓度比.对每种三元体系,选取4种摩尔比和7个水平的总浓度进行组合,得到28种组成,3种三元体系共84种组成.对于四元体系的组成选取,以摩尔比r=n(Li+)∶n(Na+)∶n(K+)表示3种阳离子的浓度比,选取3种摩尔比和8个水平的总浓度进行组合,得到24种组成.三元体系和四元体系渗透压的模拟值和文献参考值对比如图4~图7所示.
对比图4~图7和表4中的误差分析结果可知,对于4个体系,MEF方法的预测效果和误差整体而言比FS方法更好.这说明本文对OPAS方法进行的此处改进能够从二元推广到多元,并不影响其相对于FS方法的精度优势.
对3种三元体系,FS方法的误差都比二元体系更大.如图4~图6及表4所示,3种体系的FS方法计算值误差大小为LiCl-KCl-H2O≈LiCl-NaCl-H2O<NaCl-KCl-H2O.对比图3中二元体系的情况,LiCl的FS方法计算值给出偏低的结果,而NaCl和KCl的FS方法计算值给出偏高的结果,因此,LiCl-KCl-H2O和LiCl-NaCl-H2O体系整体FS方法计算值误差,相对于NaCl-KCl-H2O体系较低,可能是一定程度上的误差抵消的结果.
如图7所示,对于四元体系LiCl-NaCl-KCl-H2O,无论是FS方法还是MEF方法,精度都略好于3种三元体系.对于含有LiCl的体系,FS方法预测的渗透压在中等浓度时出现误差显著增高的现象,并有LiCl含量越高误差峰值出现越早的趋势,这可能是误差抵消程度更小的缘故.

Fig.4 Simulated and referenced osmotic pressures of ternary system LiCl⁃NaCl⁃H 2O

Fig.5 Simulated and referenced osmotic pressures of ternary system LiCl⁃KCl⁃H 2O
另一方面,通过分析体相溶液的离子-水径向分布发现,FS方法的高误差可能与微观结构中离子水合层的性质有关.图8展示了4.4 mol/kg的3种二元溶液和不同摩尔比的3.0和6.0 mol/kg LiCl-KCl-H2O溶液体相的离子-水径向分布函数(RDF).
对以上RDF曲线进行分析.(1)如图8(A)所示,二元体系中,存在第一水合层距离LiCl-H2O<NaCl-H2O<KCl-H2O的关系;(2)如图8(B)和(C)所示,相较于二元体系,三元体系LiCl-KCl-H2O的水合层类似于LiCl-H2O和KCl-H2O水合层的叠加,一方面使0.4 nm范围以内的结构更加复杂,另一方面RDF函数随距离收敛得更慢,指示水合层对体相溶液的影响加强.
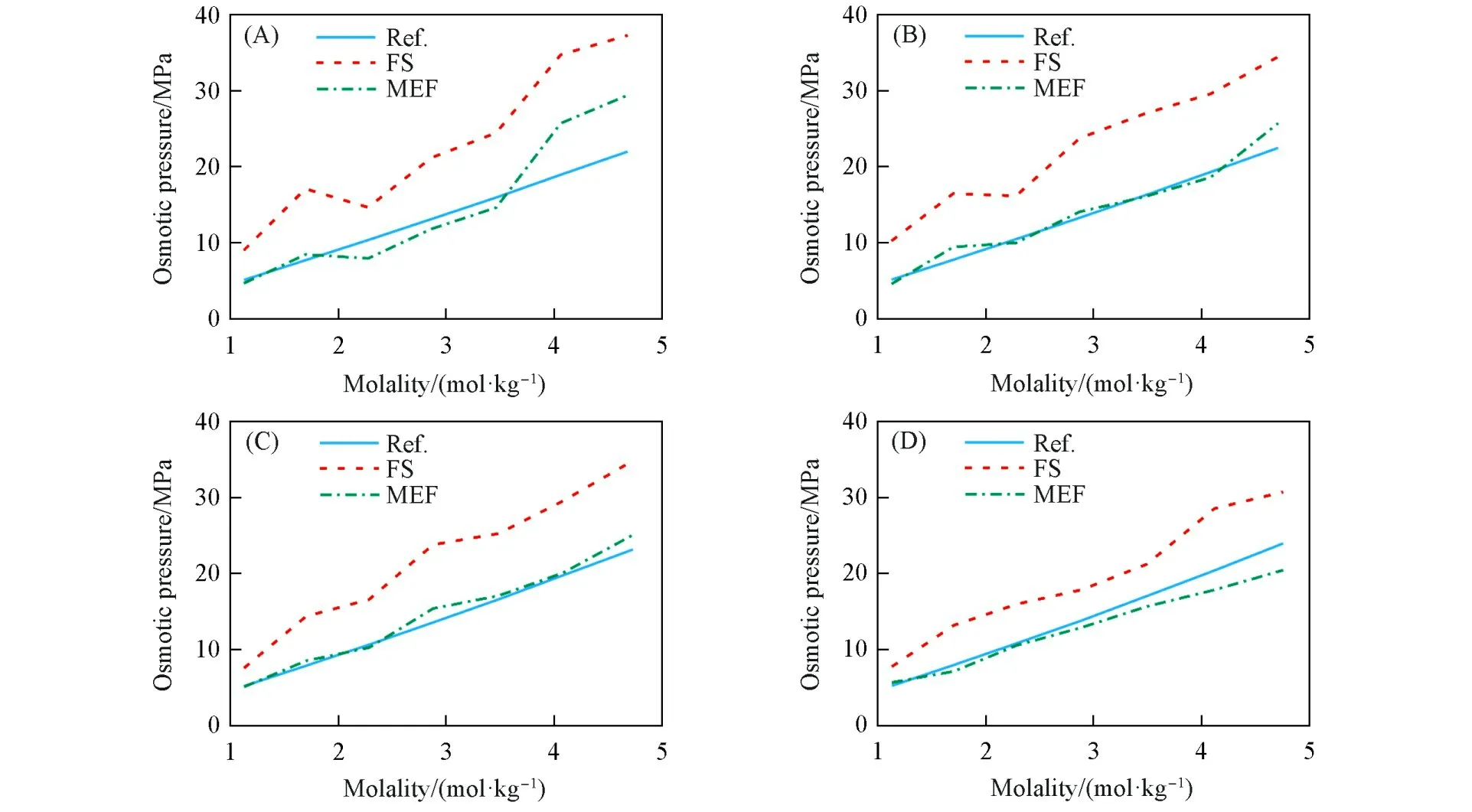
Fig.6 Simulated and referenced osmotic pressures of ternary system NaCl⁃KCl⁃H 2O

Fig.7 Simulated and referenced osmotic pressures of quaternary system LiCl⁃NaCl⁃KCl⁃H 2O

Table 4 Error analysis of computed osmotic pressures of ternary and quaternary systems

Fig.8 Radial distribution functions of water⁃ion pairs of binary systems and ternary system LiCl⁃KCl⁃H 2O
同时,结合FS方法计算的渗透压的误差分析显示以下现象:(1)3个二元体系之间,FS方法的相对偏差LiCl<NaCl<KCl;(2)三元溶液体系FS方法的误差比二元体系更大,且即使存在一定程度的误差抵消,FS方法的计算值也都普遍偏高.
对照以上现象表明,水合层的厚度以及其对体相溶液的影响程度,很大程度上影响了膜与离子间的作用力,并反映在FS方法的误差上.这一方面说明在加入了虚拟膜之后,溶液结构问题一定程度上变得更加复杂;另一方面这指示了对于渗透压相关问题,可能需要开发专门的力场形式或参数.如结合非键相互作用修正(NBFIX)技术[25,26],通过精细调整力场参数以调整水合层的性质.考虑到本文提出的MEF方法具有较好的通用性和可扩展性,将二者仔细地结合可作为一种有益的尝试.
三元体系和四元体系的主要数值结果列于表5.其中渗透压参考值来自文献[44~46].
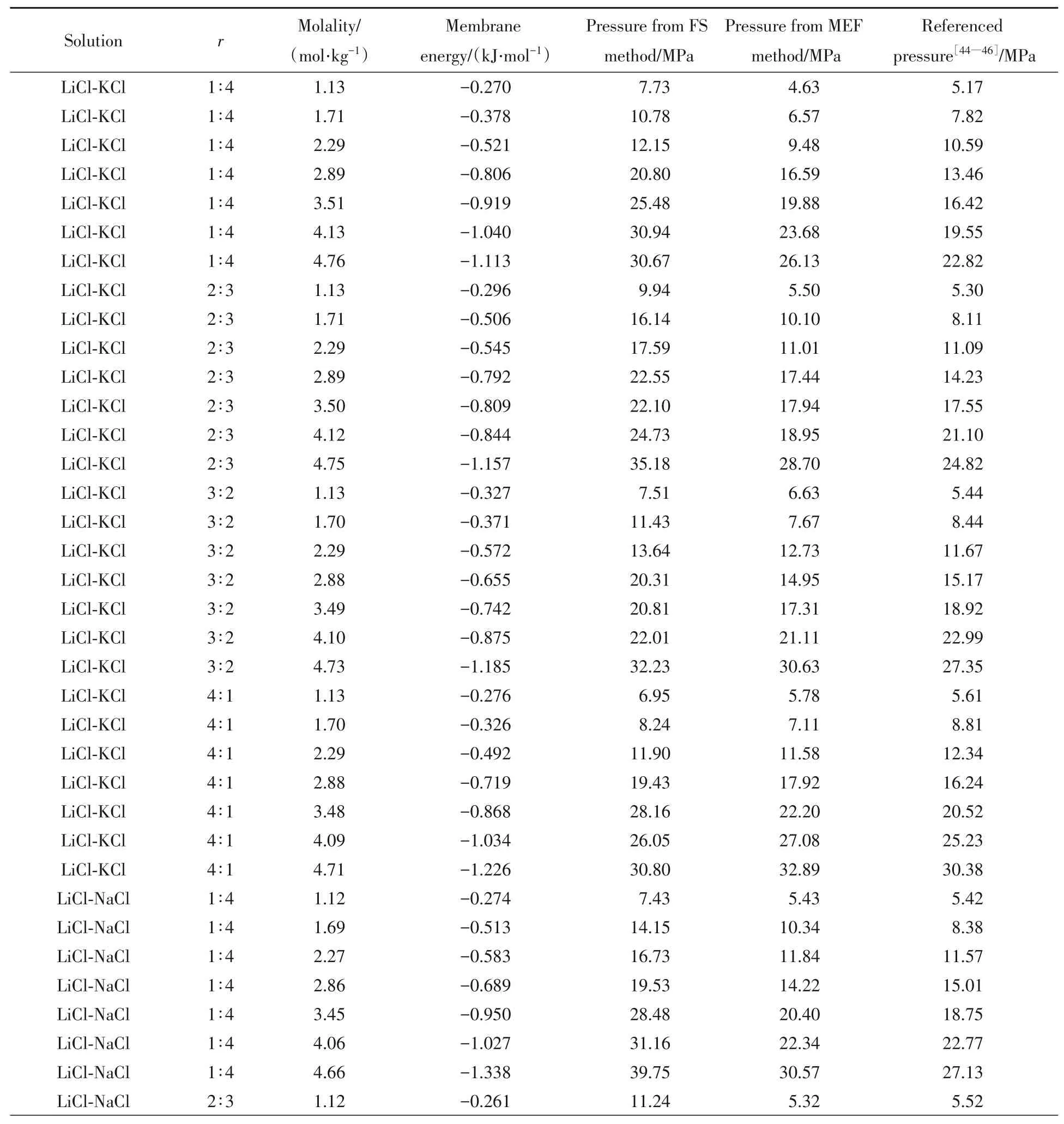
Table 5 Main numeric results of ternary solution simulations
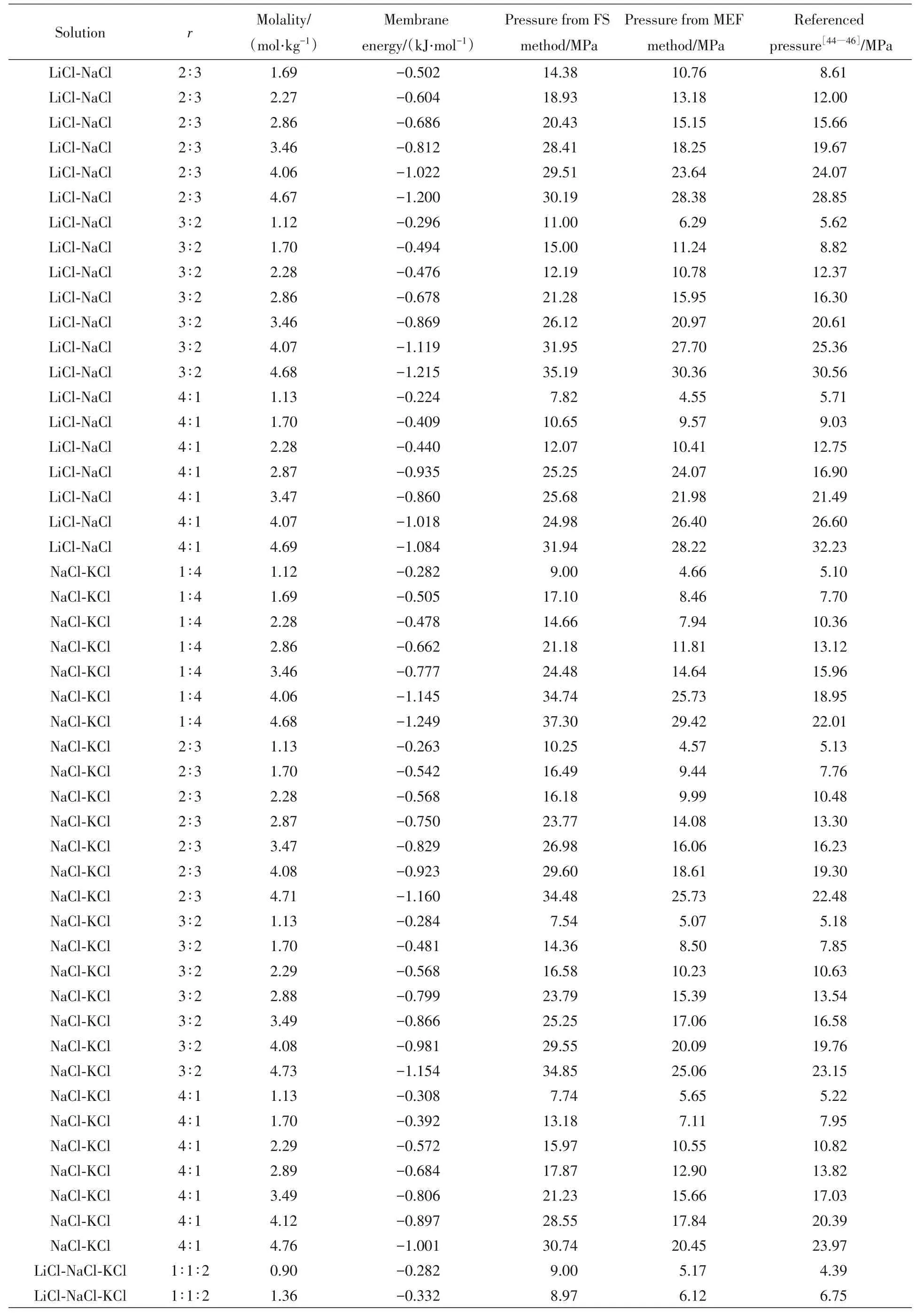
Continued

Continued
3 结 论
通过分子动力学模拟结合OPAS方法研究了LiCl-NaCl-KCl-H2O溶液体系及其子体系的渗透压.使用两种渗透压的计算方法计算了不同组成浓度溶液的渗透压,并与文献值作对比.结果表明,两种渗透压的计算方法均能展示出渗透压随组成变化的变化趋势,具有定性或半定量的预测效果,其中MEF方法的精度比FS方法更好.但二者在精确预测混合盐溶液的渗透压方面仍有不足,一方面来自于分子动力学模拟本身存在的随机性;另一方面,误差分析表明,由体相溶液和晶体溶解度问题开发的分子力场参数并非完全适用于本工作的渗透压问题,存在较大的改进空间.使用OPAS方法结合对分子力场参数的特定优化,能够显著提高对特定类型溶液渗透压和活度的预测精度,但这类方法往往缺乏一定的通用性.考虑到本工作提出的MEF方法对一系列不同组成和浓度的溶液展现出的通用性,将二者结合可作为进一步改进和优化OPAS方法,以及更准确地研究水盐混合溶液渗透压的积极尝试.
