考虑Duschinsky转动效应的电荷转移速率理论
2016-11-12陈九菊
陈九菊
(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)
考虑Duschinsky转动效应的电荷转移速率理论
陈九菊
(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)
根据费米黄金规则,在位移简谐振子近似下,采用路径积分方法推导了一个高斯类型的关联函数形式,并最终发展了一个考虑Duschinsky转动效应的电荷转移速率理论。文中方法的优点在于不需要计算复杂的弗兰克-康登因子,从而将Duschinsky转动效应自然地包括到理论形式之中。在位移简谐振子近似下,所发展的电荷转移速率形式可以回归到已有的电荷转移速率理论。
电荷转移;路径积分;Duschinsky转动;费米黄金规则;关联函数
理论描述电荷转移过程一直是凝聚态领域一个研究方向[1]。从给体到受体的标准电荷转移图像需要考虑这两个态之间的电子耦合,并受到核运动的影响。通常情况下,核自由度被描述为简谐振子,从而形成热库。基于这种图像,一些数值方法被发展出来,其中包括直接路径积分方法[2-3]、质心近似[4]以及其他非微扰方法[5-8]。这些方法通常被用于处理一维反应事件,这种事件会与简谐振子构成的热库发生相互作用。然而,实际化学反应过程中的反应隧穿需要包括几个自由度,因此需要全量子力学来处理。在这种情况下,费米黄金规则对于速率理论是一个有效的工具[9-10],其常常被用于分析实验上的电荷转移速率[11]。
费米黄金规则方法在计算体系的电荷转移速率时具有一定的局域性。首先,因为费米黄金规则是基于一级含时微扰理论,所以其要求初态与末态之间的电子耦合必须足够小。其次,初始势能面的布局在非绝热弛豫过程中要始终保持在热平衡。在这两个条件下,费米黄金规则方法将电荷转移速率描述为对某一个函数的时间积分,但很难精确求解[12]。随后,Lin等人进一步发展了该电荷转移速率的表达形式,使之可以精确用于计算电荷转移速率常数[13]。
电荷转移是化学反应过程中的一个重要的动力学过程,因此,发展电荷转移速率理论对于理解电荷转移过程至关重要,也是理论化学一个研究方向。理论工作者发展了一些适用于任意电子耦合强度的电荷转移理论,这些理论可以将非绝热极限和绝热极限下的电荷转移速率联系起来。然而,在电荷转移过程中,势能面会在电荷转移时发生转动,这被称之Duschinsky转动效应。
Duschinsky转动效应在无辐射过程中至关重要[14],而电荷转移过程就是其中一个无辐射过程。如何在电荷转移速率理论中考虑Duschinsky转动效应是一个难题。本论文的目的就是根据路径积分方法将基于费米黄金规则的电荷转移速率进行重新推导,并把Duschinsky转动效应包含到该电荷转移速率形式中。
1 考虑Duschinsky转动效应的电荷转移速率
根据费米黄金规则,一般的量子力学电荷转移速率具有以下形式[13,15]:
(1)
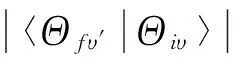
(2)

(3)
同时,初态的分布函数可以表达为
(4)
(5)
其中Gj具有形式
(6)
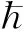
(7)
然后
(8)
(9)
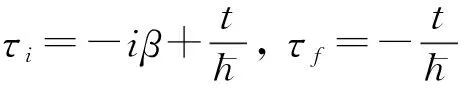
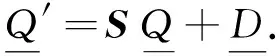
(10)
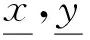
(11)
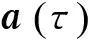
(12)
和
(13)
就可以得到以下两个数学形式
(14)

(15)
当定义矩阵
(16)
(17)
(18)
并把方程(14)和(15)带入方程(11)后,关联函数的形式就可以表达为
(19)
这里,每一个振动模式的初态和末态频率被认为是一致的。
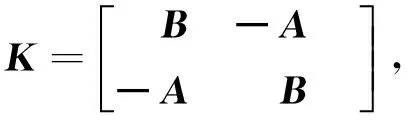
(20)
(21)
(22)
关联函数就变为
(23)
在把方程(8)和(23)代入到方程(5)后,最终的考虑Duschinsky转动效应的电荷转移速率形式为
(24)
2 没有考虑Duschinsky转动效应的电荷转移速率形式
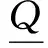

(25)
显然,方程(16)~(18) 变为对角矩阵。当定义一个新的对角矩阵,即
(26)
关联函数就变为
(27)

(28)
(29)
通过结合方程(27)~(29)和(8),就可以得到
(30)
把方程(30)代入到方程(5),就可以得到Lin等人推导的电荷转移速率形式[13],即
(31)
3 结 论
本文采用路径积分技术,推导了一个高斯类型的关联函数,从而最终发展了一个考虑Duschinsky转动效应的电荷转移速率理论。本文发展的方法不再需要计算复杂的弗兰克-康登因子在位移简谐振子近似下,可以回归到文献上已有的没有包含Duschinsky转动效应的电荷转移速率理论。因此,该方法更具有普适性。该方法为今后数值研究Duschinsky转动效应对电荷转移的影响提供了理论基础。
[1]ULSTRUP J.Charge Transfer Processes in Condensed Media[M].Berlin:Springer-Verlag,1979.
[2]MAKRI N.Quantum dissipative dynamics:A numerically exact methodology[J].J Phys Chem A,1998,102:4414-4427.
[3]GOLOSOV A A,FRIESNER R A,Pechukas.Reduced dynamics in spin-boson models:A method for both slow and fast bath[J].J Chem Phys,2000,112:2095-2105.
[4]GEVA E,SHI Q,VOTH G A.Quantum-mechanical reaction rate constants from centroid molecular dynamics simulations[J].J Chem Phys,2001,115:9209-9222.
[6]POMYALOV A,TANNOR D J.The non-Markovian quantum master equation in the collective-mode representation:Application to barrier crossing in the intermediate friction regime[J].J Chem Phys,2005,123:204111.
[7]MAKRI N.Time-dependent quantum methods for large systems[J].Annu Rev Phys Chem,1999,50:167-191.
[8]MILLER W H.Spiers memorial lecture quantum and semiclassical theory of chemical reaction rates[J].Faraday Discuss,1998,110:1-21.
[9]FAIN B.Theory of Rate Processes in Condensed Media[M].Berlin:Springer-Verlag,1980.
[10]WEISS U.Quantum Dissipative Systems.2nd ed[M].Singapore:World Scientific,1999.
[11]BIXON M,JORTNER J.Electron transfer-from isolated molecules to biomolecules[J].Adv Chem Phys,1999,106:35-202.
[12]NERIA E,NITZAN A.Semiclassical evaluation of nonadiabatic rates in condensed phases[J].J Chem Phys,1993,99:1109-1123.
[13]LIN S H,CHANG C H,LIANG K K,et al.Ultrafast dynamics and spectroscopy of bacterial photosynthetic reaction centers[J].Adv Chem Phys,2001,121:1-88.
[14]LIN S H.Rate of interconversion of electronic and vibrational energy[J].J Chem Phys,1966,44:3759-3767.
[15]JORTNER J.Temperature dependent activation energy for electron transfer between biological molecules[J].J Chem Phys,1976,64:4860-4867.
[责任编辑:刘文霞]
Charge transfer rate formalism with Duschinsky rotation effect
CHEN Jiuju
(College of Electrical and Information Engineering,Heilongjiang Institute of Technology,Harbin 150050,China)
Based on the Fermi-golden rule,the charge transfer rate in the displaced oscillator case has ever been derived,but the Franck-Condon factor has been explicitly evaluated.In the present paper,a new formalism for charge transfer rate with Duschinsky rotation effect is developed through the path integral of Gaussian type correlation function.The advantage of the present path-integral formalism is that it is no longer to compute the Franck-Condon factor and the Duschinsky rotation effect can be easily included.The new charge transfer rate formalism can easily go back to the previous formalism under the displaced oscillator approximation.
charge transfer; path integral; Duschinsky rotation; Fermi-golden rule; correlation function
10.19352/j.cnki.issn1671-4679.2016.05.010
2016-02-29
黑龙江工程学院青年科学基金资助项目(2014QJ10)
陈九菊(1981-),女,讲师,硕士,研究方向:半导体器件.
O649
A
1671-4679(2016)05-0034-04
