对称和不对称分子谐波辐射与其结构的内在关系

于术娟，刘竹琴，曹冬梅，刘艳峰，李雁鹏

（延安大学物理与电子信息学院，陕西延安716000）

0 引言

原子和分子的高次谐波产生［1-2］是实验和理论研究的热点。高次谐波在阿秒科学中有重要应用［3-4］，如对电子结构和动力学的阿秒探测等［5-6］。高次谐波产生过程可以用一个半经典的三步模型来很好地理解［7］：1）通过隧穿使活性电子电离；2）电子在激光场中的传播；3）释放的电子通过发射高能光子复合到束缚态。

本文通过改进偶极矩的计算来探讨这个问题。随着有效电荷和核间距等分子参数变化，本文选择最简单的对称双原子分子和不对称双原子分子HeH2+作为靶分子。通过虚实演化方法，得到了对称分子和不对称分子HeH2+精确的基态波函数数值表达式。利用数值的基态波函数，计算了基态和连续态之间的跃迁偶极矩。对于对称分子，比较计算得到的奇次偶极矩与谐波频谱，对于不对称分子HeH2+，比较计算得到的奇次偶极矩与奇次谐波频谱及谐波极化。并都与纯解析方法得到的跃迁矩阵元进行对比。

1 数值和解析方法

2 数值结果和讨论

图1 中，比较了核间距R=1.7 a.u.的对称分子在θ=10（o实线）、θ=40（o虚线）和θ=70（o点虚线）的奇次谐波谱及对应的数值和解析偶极矩曲线。其中，图1（a）的精确谐波谱是通过二维含时薛定谔方程得到，精确谐波谱展示一个显著的最小值，这个最小值是由两中心干涉效应引起的，在谐波谱最小值对应的谐波阶上，通过式（9）得到的图1（b）中改进偶极矩曲线也显示了一个显著的最小值，如垂直箭头所示。相比之下，通过式（6）得到的图1（c）中解析偶极矩的最小值位置与谐波谱上的最小值有显著差异，且随着取向角增大，差异更明显。这些结果证明了数值方法计算的偶极矩是适用的。同时，对其他核间距进行了模拟，结果如图2 和图3所示，随着核间距R的改变，改进的数值偶极矩曲线上显著的最小值都与奇次谐波谱上最小值对应的谐波阶符合得很好。然而，在某些情况下，纯解析偶极矩曲线上最小值的位置与谐波谱上最小值对应的谐波阶有显著不同。

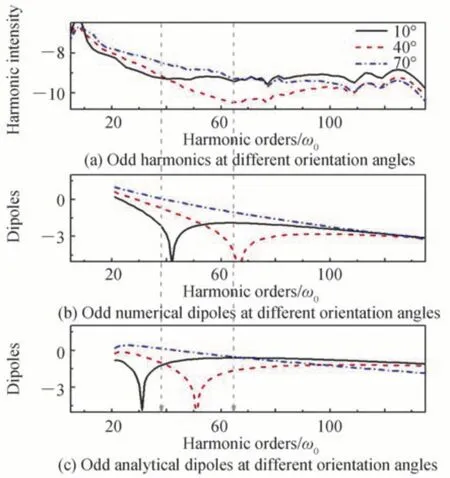
图1 核间距R=1.7 a.u.的对称分子 的谐波谱、数值和解析偶极子的比较Fig.1 The comparation of the harmonic spectra and corresponding numerical and analytical dipoles for symmetrical molecule with the internuclear distance R=1.7 a.u.

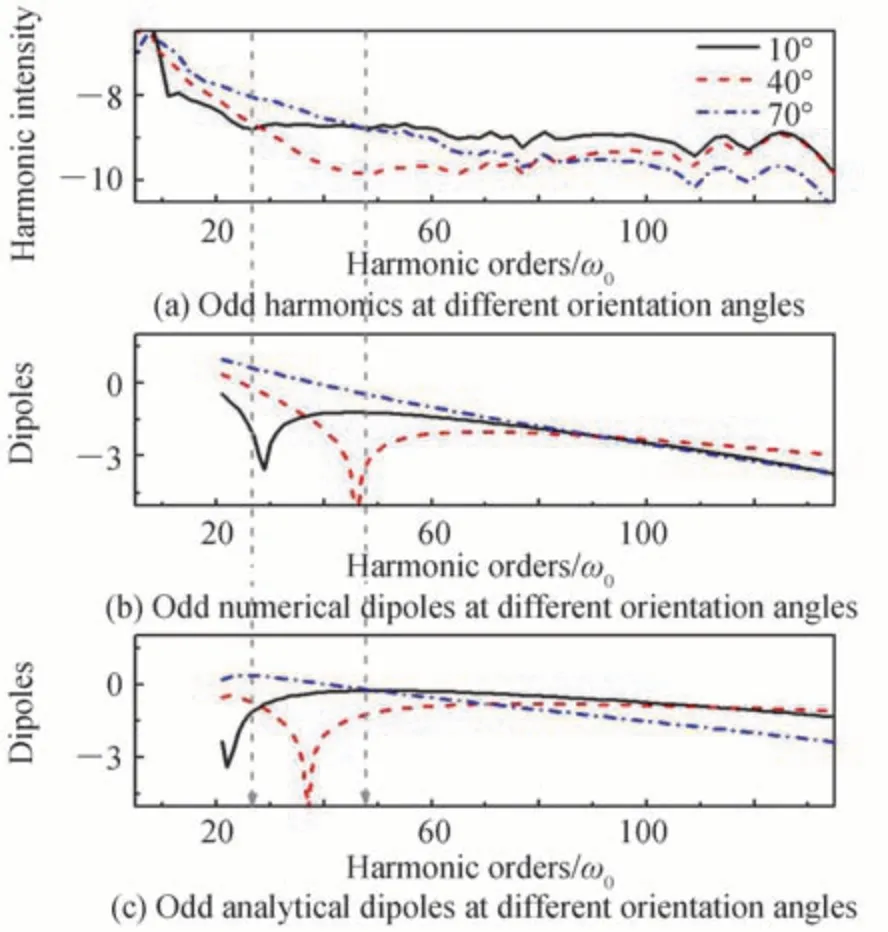
图2 核间距R=2 a.u.的对称分子 的谐波谱、数值和解析偶极子的比较Fig.2 The comparation of the harmonic spectra and corresponding numerical and analytical dipoles for symmetrical molecule with the internuclear distance R=2 a.u.

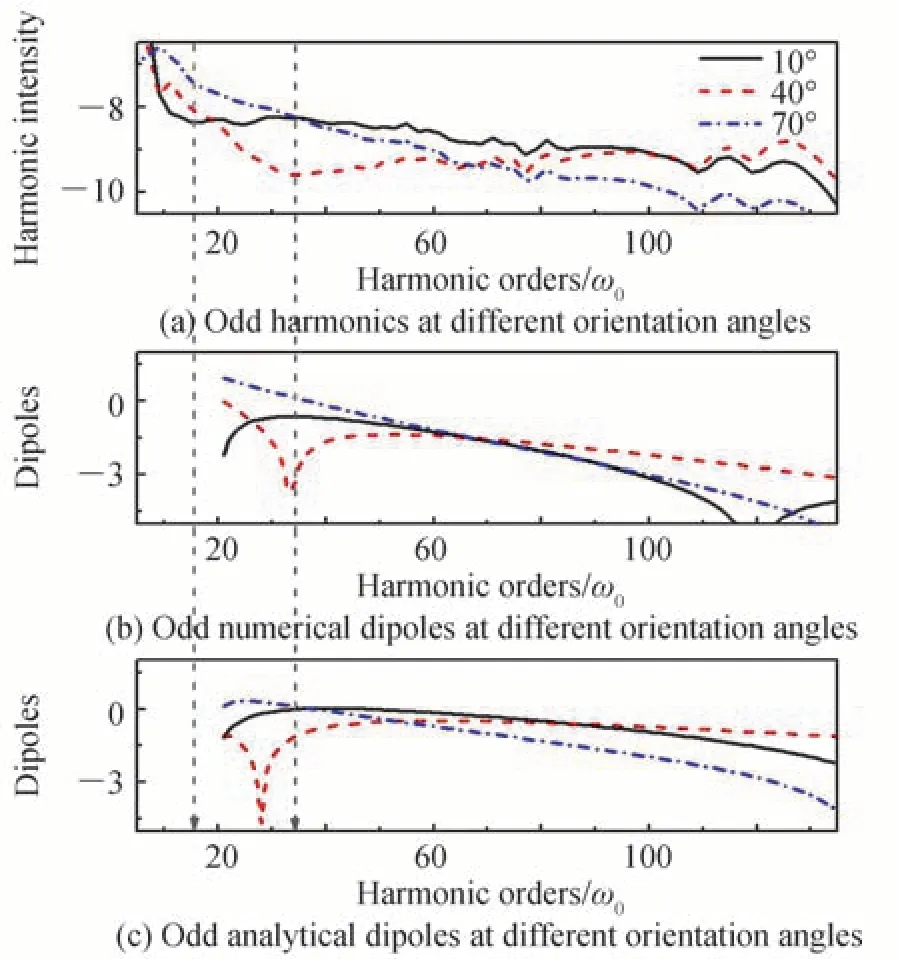
图3 核间距R=2.3 a.u.的对称分子 的谐波谱、数值和解析偶极子的比较Fig.3 The comparation of the harmonic spectra and corresponding numerical and analytical dipoles for symmetrical molecule with the internuclear distance R=2.3 a.u.

值得注意的是，图3 中夹角为10o时，偶极矩未出现最小值，但是在谐波谱中标出了最小值，由于高次谐波产生过程可用半经典三步模型来很好地理解［7］，在复合过程中，电子将降低其能量并释放出高能光子ω。这个过程被称为高次谐波产生，如果电子的返回制动能为Ep，则光子的能量为ω=Ep+Ip，由于电子的制动能大于零，那么光子的返回能量总是接近或大于Ip（阈上谐波），跃迁偶极矩符合半经典三步模型的描述，夹角为10o时，偶极矩只计算了与阈上谐波对应的跃迁偶极矩数据，因此未出现最小值。然而，在实验和数值模拟中，发射的光子能量ω可以小于Ip，称之为阈下谐波，因此谐波谱既包括阈上谐波也包括阈下谐波，图3谐波谱是通过数值模拟得到的，并且谐波谱上的最小值位置位于阈下谐波，所以在谐波谱中标出了最小值。

不对称模型HeH2+分子的相关结果如图4～6所示。已有研究结果表明，对于具有小核间距R的模型HeH2+分子，式（7）预言的奇次偶极矩展示出显著的最小值。然而，这个最小值在奇次谐波谱中消失。相反，奇次谐波的极化曲线上的最大值对应的谐波阶却出现在奇次偶极矩最小值处。因此，谐波的极化可以作为探测偶极矩中最小值位置的工具。偶极矩上的最小值解码了分子结构的信息，在不对称分子轨道成像中有潜在的应用。然而，在某些情况下，偶极矩曲线中最小值的位置与最大极化的谐波阶并不一致，应用谐波的极化测量作为判断偶极矩最小值的工具对其进行研究。

比较了有效电荷比为Z1/Z2=1.5、核间距R=2 a.u.的不对称模型HeH2+分子在不同角度的奇次谐波谱、谐波极化和偶极矩曲线，如图4。其中，图4（a）的精确谐波谱通过二维含时薛定谔方程得到，并且精确谐波谱曲线没有显著的最小值，由于谐波的极化可以作为探测偶极矩中最小值位置的工具，图4（c）的谐波极化曲线出现了一个显著的最大值。尤其是，最大极化对应的谐波阶，在该谐波阶上，通过式（10）得到的图4（b）中改进的偶极矩曲线上显示了一个显著的最小值，如垂直箭头所示。相比之下，通过式（7）得到的图4（c）中解析偶极矩上的最小值位置与谐波极化最大值有显著差异，且随着取向角增大，差异更明显。这些比较揭示了偶极矩曲线上最小值和极化最大值之间存在着一一对应的关系。由于式（7）中的基态波函数有一个粗略的近似，导致通过式（7）计算得到的偶极矩曲线上最小值的位置低估了10 到30 谐波阶。

图4 Z1/Z2=1.5 及核间距R=2 a.u.的不对称分子He 谐波的极化、谐波谱和偶极子的比较Fig.4 The comparation of the ellipticity of harmonic，harmonic spectra and corresponding dipole for asymmetric molecule He with Z1/Z2=1.5 and internuclear distance R=2 a.u.

为了验证本文结果，固定核间距R的值，改变有效电荷比Z1/Z2的值，对其他分子参数进行了模拟，如图5所示。改进偶极矩中最小值的位置与最大极化出现的谐波阶基本一致。相比之下，在某些情况下，纯解析偶极矩中最小值的位置与最大极化的谐波阶有显著不同。对于图5（b）中θ=40o的中间角情况，改进的数值偶极矩曲线上最小值位置与最大极化出现的谐波阶不对应，在这种情况下，改进的数值偶极矩与谐波极化之间的对应关系不是很明显。但是与纯解析偶极矩相比，改进的数值偶极矩的最小值更接近极化最大值出现的谐波阶。此外，固定Z1/Z2的值，改变核间距R的值，如图6所示。在扩展模拟中也观察到了偶极矩、谐波谱和谐波极化之间的密切关系。应该强调的是，尽管虚实演化法的使用改善了奇偶谐波极化和数值奇偶偶极矩之间的一致性，但是在偶极矩最小值的位置上仍有一些区别。原因是在计算偶极矩时，这些差异起源于具有有效动量pk的连续电子的平面波近似，库仑效应没有得到很好地描述。

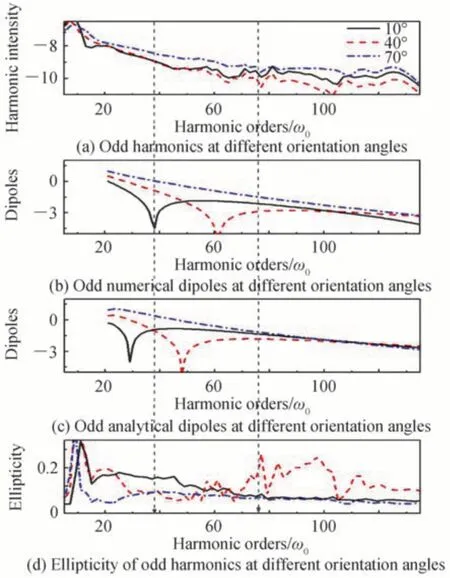
图5 Z1/Z2=2 及核间距R=2 a.u.的不对称分子He 谐波的极化、谐波谱和偶极子的比较Fig.5 The comparation of the ellipticity of harmonic，harmonic spectra and corresponding dipole for asymmetric molecule He with Z1/Z2=2 and internuclear distance R=2 a.u.

图6 Z1/Z2=2 及核间距R=1.7 a.u.的不对称分子He 谐波的极化、谐波谱和偶极子的比较Fig.6 The comparation of the ellipticity of harmonic，harmonic spectra and corresponding dipole for asymmetric molecule He with Z1/Z2=2 and internuclear distance R=1.7 a.u..

对于不对称分子，有两种高次谐波产生路径导致奇（偶）次谐波的释放，可以用和来表示，通常，奇（偶）次谐波的主要贡献来自路径然而，当沿激光偏振方向的两中心干涉效应导致奇（偶）次平行谐波在路径上被强烈抑制时，另一条路径开始对这些谐波的产生有显著影响，导致两条路径相互干涉，这种干涉改变了平行谐波的相位，并将其与垂直谐波区分开来。奇（偶）次谐波展示出高的椭偏率，但本文模拟的不同参数下的HeH2+分子，偶次谐波通常整体较弱，并且偶次跃迁偶极矩不显示最小值，只在低阶谐波观察到偶次谐波高的椭偏率，偶次谐波的极化峰现象不显著，只有奇次谐波谱在特定的谐波阶展示了显著的极化最大。因此本文只关注奇次谐波。

3 结论

本文主要通过数值和解析相结合的方法研究了对称和不对称分子谐波辐射与其结构的内在关系。应用虚实演化法得到了对称分子和不对称分子HeH2+的基态波函数的数值表达式。利用数值的基态波函数，计算了基态和连续态之间的跃迁偶极矩，进一步将跃迁偶极矩减去跟核间距成比例这项。模拟结果表明，对于对称分子，用虚实演化方法计算得到的基态波函数显著地改善了奇次偶极矩和奇次谐波谱的一致性，尤其在不同核间距下，改进的偶极矩最小值与高次谐波谱上的最小值符合地很好。对于不对称分子HeH2+，由于在不对称分子的高次谐波谱中通常不存在最小值，谐波的极化测量可以作为探测最小值位置的工具，得到的基态波函数显著地改善了奇偶偶极矩最小值和奇偶谐波极化最大值之间的一致性。这些现象揭示了再结合过程在对称分子和不对称分子的谐波辐射中起着关键作用，研究结果对奇偶谐波辐射在不对称分子超快探测中的作用具有一定意义。