基于MATLAB GUI渐开线变位直齿轮参数化全齿廓建模分析*

曹东江，尚 鹏，肖立宁，赵长生，崔宏涛

(航空工业庆安集团有限公司，陕西 西安 710077)

0 引 言

齿轮传动是一种非常重要的传动方式，以其传动效率高，工作可靠，结构紧凑等特点被广泛应用于机械、汽车、航空及航天等诸多领域[1]，在现代机械工业发展中占据显要地位。随着计算机技术的发展，人们更倾向于应用各种先进的分析软件对齿轮进行仿真研究，比如进行齿轮接触变形分析、动力学分析、载荷能力分析等。为了得到满意的仿真结果，都需要对齿轮进行三维准确建模[2]。鉴于在常规齿轮CAD建模过程中，存在同类齿轮因参数不同要反复建模的问题[3]，希望寻求对齿轮进行快捷的精确参数化建模。

目前，关于齿轮参数化建模可参考的文献已经有很多,但也存在诸多问题，早期论文对全齿廓曲线的绘制，尤其是对齿根过渡曲线的绘制，为了规避其建模方程的复杂性，大多采用圆弧代替的画法[4-7]。经过相关学者的进一步研究，后来一些文献[8-11]，提出了针对齿条型刀具加工齿轮形成的齿廓过渡曲线准确的参数化方程，继而提出了比较详细的齿轮参数化全齿廓建模方法[12]，但是对齿轮型刀具切制齿轮并形成全齿廓参数化精确模型少有描述，或者有描述但并没有明确齿廓过渡曲线起始和终止参量角度大小[13-14]。

基于上述研究，笔者从齿轮啮合原理的角度分析过渡曲线的形成方法，将机器人学中齐次坐标变换的方法应用到齿轮啮合运动学中，利用齿廓法线法建立齿廓过渡曲线的参数化方程。针对典型的齿条型和齿轮型刀具，并且区分其刀具齿角是尖角或圆角的不同，推演其范成加工齿轮时形成的各自的过渡齿廓曲线参数方程，并给出齿根过度曲线方程参量的起始和终止角度，最后应用MATLAB GUI 对齿轮进行全齿廓建模计算，并将数据导入CATIA软件，形成准确的轮齿参数化三维模型，为后续齿轮性能仿真及应力分析等研究奠定基础。

1 全齿廓参数化方程建立

1.1 齿轮渐开线精确建模

如图1所示：渐开线齿轮一个完整齿廓主要由bc,cd,de,ef四段曲线组成，其中bc为齿顶圆弧曲线，cd为渐开线工作齿廓曲线，de为齿廓过渡曲线或齿根过渡曲线，在用范成法加工时，根据刀具齿顶形状的不同，由刀具齿顶尖角(或者圆角)形成的包络线即为齿廓过渡曲线，ef为齿沟曲线是刀具齿顶线的包络线，也叫齿根圆曲线。过渡曲线用以连接齿轮工作齿廓和齿根圆曲线，在不根切的情况下，过渡曲线和工作齿廓相切，也和齿沟曲线相切[13]。过渡曲线对于轮齿的抗弯强度计算，尤其是对于齿根的应力集中有很大影响[13]。下面分析上述各段齿廓曲线的参数化建模方法[12]。

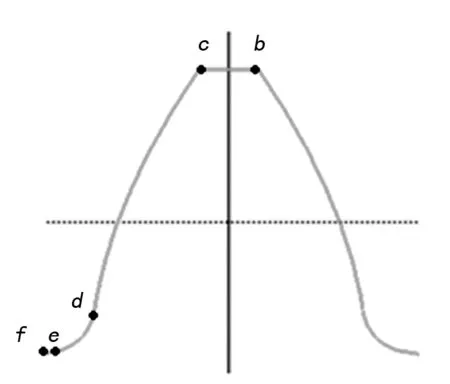
图1 齿轮全齿廓曲线

1.2 齿顶圆曲线

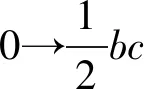
(1)

1.3 渐开线工作齿廓曲线

根据齿轮渐开线生成原理，其示意图如图3所示，推导出直角坐标系下齿轮齿廓渐开线参数方程：

(2)

式中：rb齿轮基圆半径，γ=tanαk，δ=β+invα，αk∈[αN,arccos(rb/ra)]。A点是渐开线起点，N点为齿廓渐开线与齿廓过渡曲线的连接切点。

图2 齿顶圆弧曲线

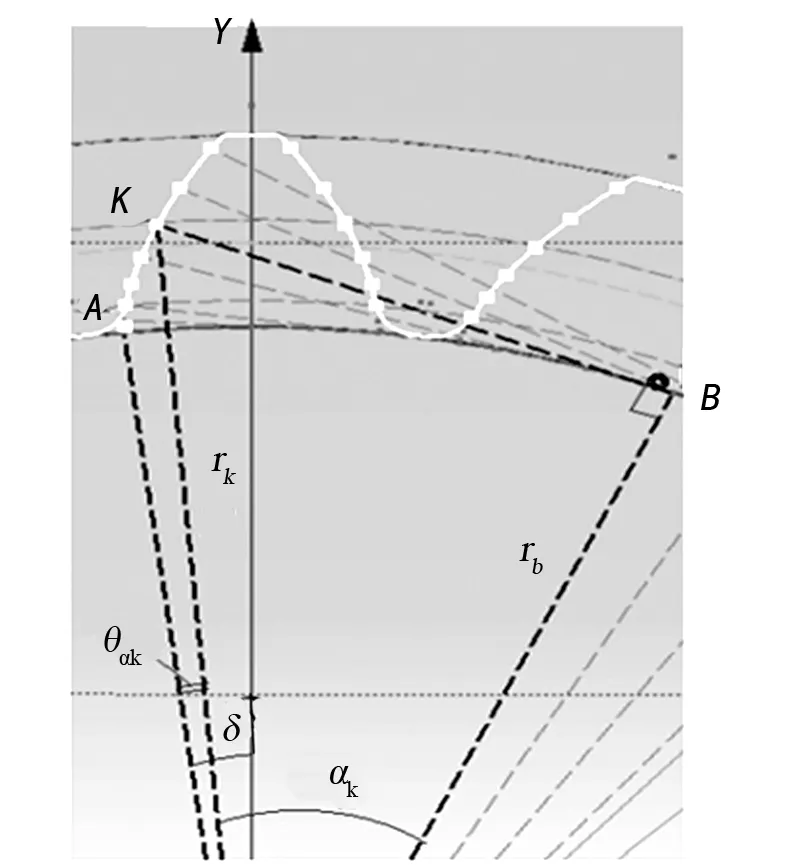
图3 渐开线齿廓曲线

1.4 齿廓过渡曲线

应用展成法加工齿轮时，根据刀具齿形形状不同，其加工出来的齿廓过渡曲线也不同。目前常用的刀具有齿条型和齿轮型刀具，刀具齿顶角又有尖角和圆角两种不同的情况。文中从齿轮啮合原理的角度推演在不同加工情形下齿廓过渡曲线的形成过程。

1.4.1 齿条型刀具

(1)刀具齿顶为尖角

当加工刀具齿顶为尖角时，其过渡曲线形成如图4所示[14]，齿条齿侧齿廓(即侧刃)为AB，齿条齿顶线(即顶刃)为AC，交点A为齿顶尖角，侧刃在A点的法线n1与节线I交于a1点，顶刃在A点法线n2与节线I交于a2点，a1a2=l。在a2点设置动坐标系S1(O1-x1,y1)和齿条固连，其x1轴沿节线I方向，y1轴沿n2方向，通过齿角A点。齿角A点在S1中的坐标为：

(3)

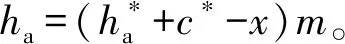
图4 齿条齿顶尖角形成的过渡曲线

在啮合过程中，齿条侧刃AB包络出齿轮渐开线齿廓A1B1，顶刃AC包络出齿轮的齿根圆弧。当齿条从右向左移动，在图4瞬时位置，法线n1与节线I交于啮合节点P，齿角A与齿轮齿廓A1点相啮合，齿条开始切制过渡曲线；齿条由这个位置继续向左移动直至l距离，此时法线n2与节线I相交于点P，在齿轮中心O2设置动坐标系S2(O2-x2,y2)随被切制齿轮旋转，齿条向左移动l距离，旋转坐标系S2相应的转过角度φ2(φ2=l/r2)，齿顶尖角A与齿根圆弧的A2点啮合(图4中虚线d点位置)，至此过渡曲线切制完成。过渡曲线即为啮合过程中齿角A在齿轮上A1、A2两点间的运动轨迹。从图4中可以看出，齿轮节线I在沿着节圆II纯滚动时，齿顶尖角A运动轨迹为旋轮线(长幅渐开线或叫延伸渐开线)，如图5中虚线所示[14]。

图5 齿廓过渡曲线

为求此过渡曲线的方程，只需将点A在S1中坐标(x1,y1)转换到与齿轮2相固连的坐标系S2上即可[13]。为了得到A(x1,y1)在坐标系S2中的坐标表示，借鉴关节机器人关节坐标的齐次变换法则[15]，将A在S1中的坐标向量表示为A(x1,y1,z1,1)T，在S2中表示为A(x2,y2,z2,1)T，因为我们现在研究的是平面坐标系，可置z1,z2为0。有：

(x2,y2,0,1)T=M21(x1,y1,0,1)T

(4)

M21为坐标转换矩阵，根据坐标齐次变换法则，需要将S2(O2-x2,y2)左旋φ2使其y2轴与S1之y1轴平行，再将坐标系S2沿y2平移r2距离至P点，再沿x2向右平移l(l=r2φ2)，此时坐标系S2与S1重合，据此变换过程可将M21表示为：

M21=Rot(z2,φ2)×Trans(0,r2,0)×

Trans(l,0,0)

(5)

其中旋转坐标变换：

平移坐标变换：

计算M21得：

M21=

(6)

由式(4)得：

(7)

将式(3)A(x1,y1)点坐标的值代入，得到齿廓过渡曲线方程：

(8)

由于φ2=l/r2，且l=hacotα，有φ2=hacotα/r2，其中α为啮合点A法线n1与节线I之间夹角，α范围α∈[α2,90°],α2为齿条齿形角。

(2)刀具齿顶为圆角

图6 齿条齿顶圆角范成运动坐标

当齿条刀具齿顶为圆角时，如图6所示[14]，齿顶圆角圆心为A，半径为ρ，它与刀具齿侧刃及齿顶刃的交界切点分别为A2和A1。当节线I与节线II作纯滚动时，由A2A1圆弧包络出来的曲线是齿廓过渡曲线，该过渡曲线是A点运动轨迹(长幅渐开线)的等距曲线[14]。

当圆角圆弧上任一点M在坐标系S1中坐标为：

(9)

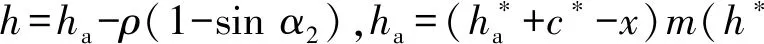
采用齿廓法线法建立啮合方程，若动点M成为啮合点，则此时过M点的齿廓法线MA必经过啮合节点P，齿条上固连坐标系S1与P点之间距离为l=r2φ2，且有：

l=O1Acotα=(h-ρsinα2)cotα

(10)

故啮合方程为：

r2φ2=(h-ρsinα2)cotα

(11)

将式(9)代入式(7)，再与式(11)联立，即可得齿廓2过渡曲线方程：

(12)

方程式(12)经转换形式可得：

(13)

式(13)与张奎晓、施火结等[8,11]计算的过渡曲线方程形式相同。当α=α2得到过渡曲线与齿廓渐开线的连接切点；当ρ=0，即齿顶角为尖角时候，h=ha，上式就变为式(8)。

1.4.2 齿轮型刀具

当采用齿轮型刀具进行展成加工，在用齿轮2包络齿轮1齿廓时，其刀具齿角A在齿轮1上的运动轨迹形成齿廓过渡曲线，如图7所示[14]，根据旋轮线理论，当齿角A为尖角时，过渡曲线为长幅外摆线，当刀具齿角A为圆角时，过渡曲线为长幅外摆线的等距曲线[13]。

(1)刀具齿顶为尖角

建立坐标系如图7所示，动坐标系S1(O1-x1,y1)随齿轮1旋转，S2(O2-x2,y2)随齿轮2旋转，齿角A位于坐标系S1之y1轴上，其坐标方程为：

(14)

式中：Ra为刀具齿轮1的顶圆半径。

利用坐标变换将S1中齿角A坐标(x1,y1)变换到坐标系S2中，即可得到被切齿轮2过渡曲线方程。

图7 齿轮刀具齿角A形成的过渡曲线

同式(4)有：

(x2,y2,0,1)T=M21(x1,y1,0,1)T

(15)

利用齐次变换，此时M21可以表示为：

(16)

将方程式(14)代入式(16)得到过渡曲线方程式：

(17)

式中：a为齿轮啮合中心距。因为齿轮型刀具和齿坯做展成运动，有r1φ1=r2φ2。

(2)刀具齿角为圆角

建立坐标系如图8所示[13]，刀具齿顶圆角圆心在A点，半径为ρ，若齿顶圆角上任一点A′为啮合点，A′在坐标系S1中的方程为：

(18)

式中：Ra为圆角刀具齿顶圆半径；γ为齿顶圆角上动点A′位置参量。

依据齿廓法线法建立啮合方程，则过啮合点A′的齿廓法线A′A必经过啮合节点P。当齿轮刀具转过角度φ1，使得P′点与P重合，则有：

故啮合方程为：

r1sin(γ+φ1)=(Ra-ρ)sinγ

(19)

将式(18)代入式(16)，再与式(19)联立，可得被加工齿轮2上的过渡曲线方程，经整理为：

(20)

图8 齿角圆角A形成的过渡曲线 图9 齿根圆圆弧曲线

1.5 齿根圆弧曲线

齿根圆弧曲线是齿根圆的上的一段曲线，半径为rf，如图9所示。

齿根圆弧曲线的参数方程为：

(21)

2 变位齿廓计算程序开发

基于MATLAB GUI 图形用户界面，依据上述齿廓参数化方程，对齿轮全齿廓进行建模计算，程序开发流程如图10所示，界面图如图11所示。

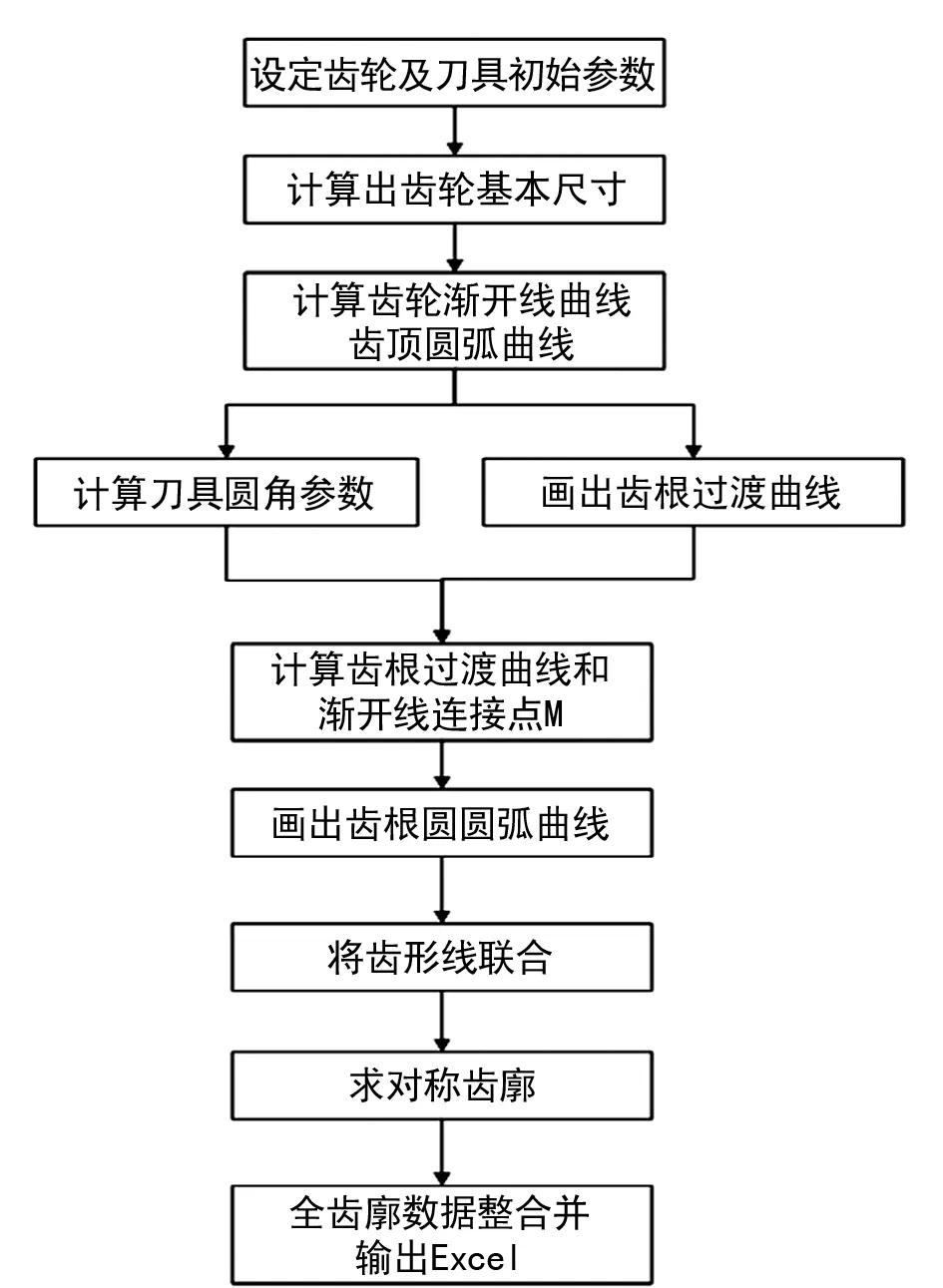
图10 变位齿轮全齿廓数据计算程序框图

图11 MATLAB GUI 用户界面图

对于界面图11(a)z=20,m=2，变位x1=0.23，应用齿条型刀具，刀具圆角分别设为r0=0,r0=0.25 m,r0=0.38 m,计算所得齿廓图形如图12、13所示。

图12 齿轮齿廓曲线(z=20) 图13 齿条刀具不同圆角形成过渡曲线比较(z=20)

对于界面图11(b)z=41,m=2,变位x1=0.2881，应用齿轮型刀具，刀具圆角分别设为r0=0,r0=0.25 m,r0=0.38 m,计算所得齿廓图形如图14、15所示。

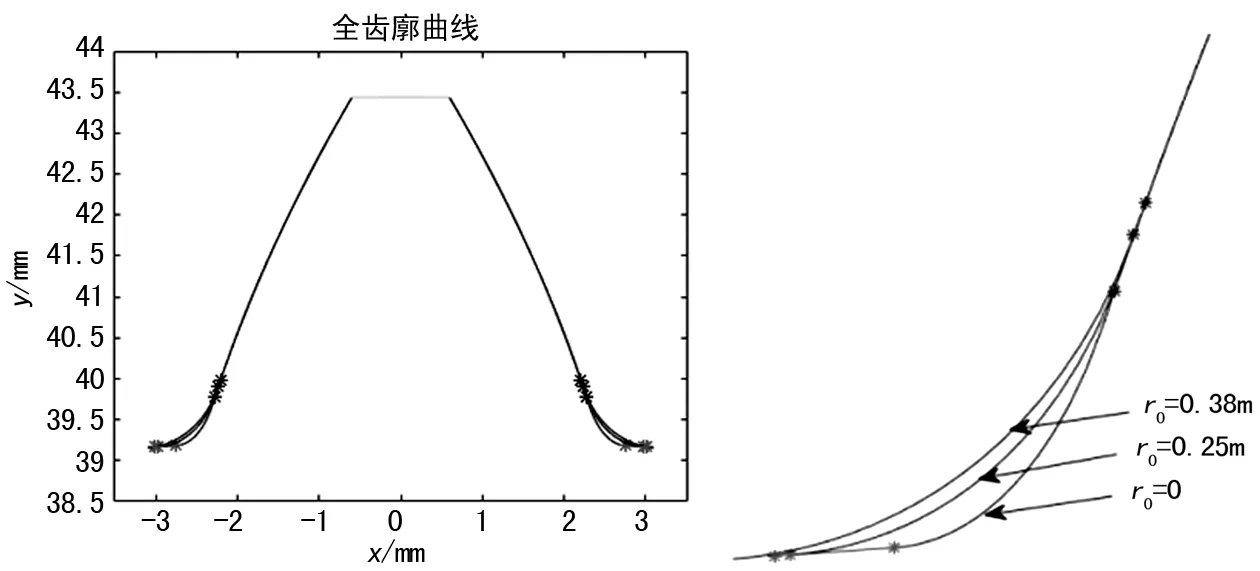
图14 齿轮齿廓曲线(z=41) 图15 齿轮刀具不同圆角形成过渡曲线比较(z=41)

对于齿轮z=41,m=2，变位x1=0.2881，分别应用齿条型和齿轮型刀具，刀具圆角均设为r0=0.38 m,计算所得齿廓图形如图16、17所示。

从仿真计算(见图12～15)结果看，对于相同的刀具，加工同样参数的齿轮，齿顶圆角r0越小，过渡曲线曲率半径越小；对于齿条型和齿轮型刀具，由于其展成方程不同，其最终形成的过渡曲线圆角也有所不同，如图16、17所示，刀具圆角同为r0=0.38 m时，齿条型刀具形成的过渡曲线曲率半径较小。当然齿廓过渡曲线圆角的大小、形状还与被加工齿轮自身参数有关[16]，这里篇幅所限，不做展开。

3 CATIA参数化变位齿轮模型设计

现有三维建模软件，包括CATIA都不具备通过直接输入参数化方程绘制出曲线的功能，因此必须将参数方程曲线转化为具体的数据点坐标，并通过某种方式将其导入到CATIA建模界面中，运用曲线样条拟合的技术，将这些齿廓坐标点连接成所要的曲线[1]，形成全齿形轮廓，最后通过圆周阵列、拉伸、拔模等操作生成齿轮实体[17]。

给定变位齿轮参数如图11(a)所示，以其中z=20,m=2,x1=0.23的小齿轮为例，应用所开发的MATLAB程序，求出全齿廓曲线数据坐标点，具体建模步骤如下所述。

(1)利用MATLAB 软件将计算齿廓数据输出为Excel.xlsx文件，并另存为GSD_PointSplineLoftFrom-Excel.xls (97-2003版本.xls文件，此文件已经集成了宏开发代码)，拷贝到CATIA目录中。

(2)打开CATIA V5R18，新建一个part文件。

(3)打开GSD_PointSplineLoftFrom-Excel.xls文件，在Excel“开始-选项-常用-”中“使用Excel时首选项”中勾选“在功能区显示“开发工具”选项卡。

(4)Excel数据列分别为(x,y,z)点坐标，在形成齿廓曲线的点坐标行前加 StartLoft和StartCurve行，在最后坐标行前加EndCurve、EndLoft、End三行，在Excel数据表格将第三列(z坐标)置为0。

(5)运行宏，在“位置”处选当前Excel文件，宏名选feuil1.main,点击“执行”，user info中输入2，确定，将坐标点导入到CATIA part文件中。

(6)因为数据输入到CATIA里面，形成的点是一系列空间点，不能直接由它们通过拔模画出齿轮实体，必须将其投影到草图平面。进入草图界面，用3D投影命令将该空间点族投影到草图平面中。

(7)在草图中，通过样条拟合技术将坐标点连接成齿廓曲线，如图18所示。

图18 将CATIA坐标点拟合成齿廓(z=20,m=2)

(8)通过圆周阵列，将单齿轮廓均布为圆周齿轮形状，如图19所示，通过拉伸形成齿轮实体模型，如图20所示。

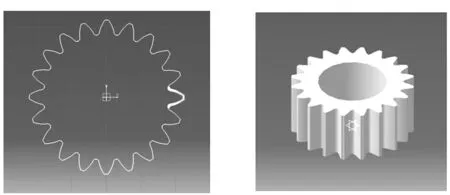
图19 将齿轮单齿廓进行圆周阵列(z=20,m=2) 图20 通过拉伸形成齿轮实体模型(z=20,m=2)

4 结 论

通过推演分析，建立了渐开线变位齿轮完整齿廓的参数化方程，通过MATLAB GUI 程序实现变位齿轮的精确求解计算和数据输出，并在CATIA软件中通过曲线拟合技术实现了齿轮实体模型的快速创建。

(1)建立了准确的全齿廓各段曲线参数化方程，明确各段曲线方程的参量取值范围，以便各曲线段准确衔接。

(2)从齿轮啮合原理出发，通过分析刀具和齿轮毛坯的范成运动过程，阐明了齿廓过渡曲线轨迹的形成；针对典型的齿条型和齿轮型刀具，及刀具齿角是尖角和圆角的不同情况，推演形成各自不同的过渡曲线方程。

(3)通过MATLAB GUI编程实现齿轮齿廓的参数化设计计算，通过对比仿真结果，显示同等条件下，刀具齿顶圆角越小，形成的过渡曲线圆角越小，对于相同刀具齿角，齿条型刀具比齿轮型刀具形成更小过渡曲线圆角。

(4)基于MATLAB GUI建立参数化齿廓数据，将其导入CATIA软件界面建立齿轮参数化精确模型，可以和ANSYS、ADAMS等动力学软件连接，便于对齿轮机构强度分析、应力分析、干涉检测等问题进行进一步的分析和研究。