大模数重载齿条中的缺陷应力场数值模拟
2020-02-26闫晓青郑卫力张银婷黄晓欢
闫晓青,郑卫力,张银婷,黄晓欢
(长江三峡通航管理局,湖北 宜昌 443002)
三峡升船机是目前世界上提升质量最大的全平衡垂直升船机,驱动机构采用齿轮齿条爬升式,齿轮齿条为重要受力构件。驱动机构最大事故载荷8 800 kN。根据《机械设计手册》,当齿轮齿条载荷较大时,应对齿轮和齿条材料、硬度和热处理工艺进行专项研究。现行方法是通过解析解与有限元法计算相结合进行校核,再通过模型试验对齿轮齿条接触应力进行论证以确定合理制造工艺。在齿轮齿条制造过程中难免存在夹杂物及其他缺陷,但设计过程并未考虑缺陷工况,很多文献研究成果表明,受力构件的损伤和失效的演化都是从夹杂物与金属基体的交界部位开始[1]。因此,本文采用Ansys Workbench建立了含有夹杂物及蚀坑的齿轮齿条接触三维有限元模型,计算各工况下齿条接触应力及剪应力,并分析了不同缺陷工况下齿条力学性能,对齿条内夹杂物含量控制、齿轮齿条运行维保提供了科学的理论依据。
1 有限元模型建立
1.1 齿轮齿条技术参数
三峡升船机齿轮齿条是驱动机构的承载元件,正常工作状态下,驱动机构小齿轮与齿条保持啮合,驱动机构载荷通过齿条传递给混凝土结构。小齿轮轴两侧的轴段支承在支承与导向机构的轴承座内,齿轮齿条结构如图1所示,齿轮齿条主要技术参数见表1。

表1 齿轮齿条主要技术参数
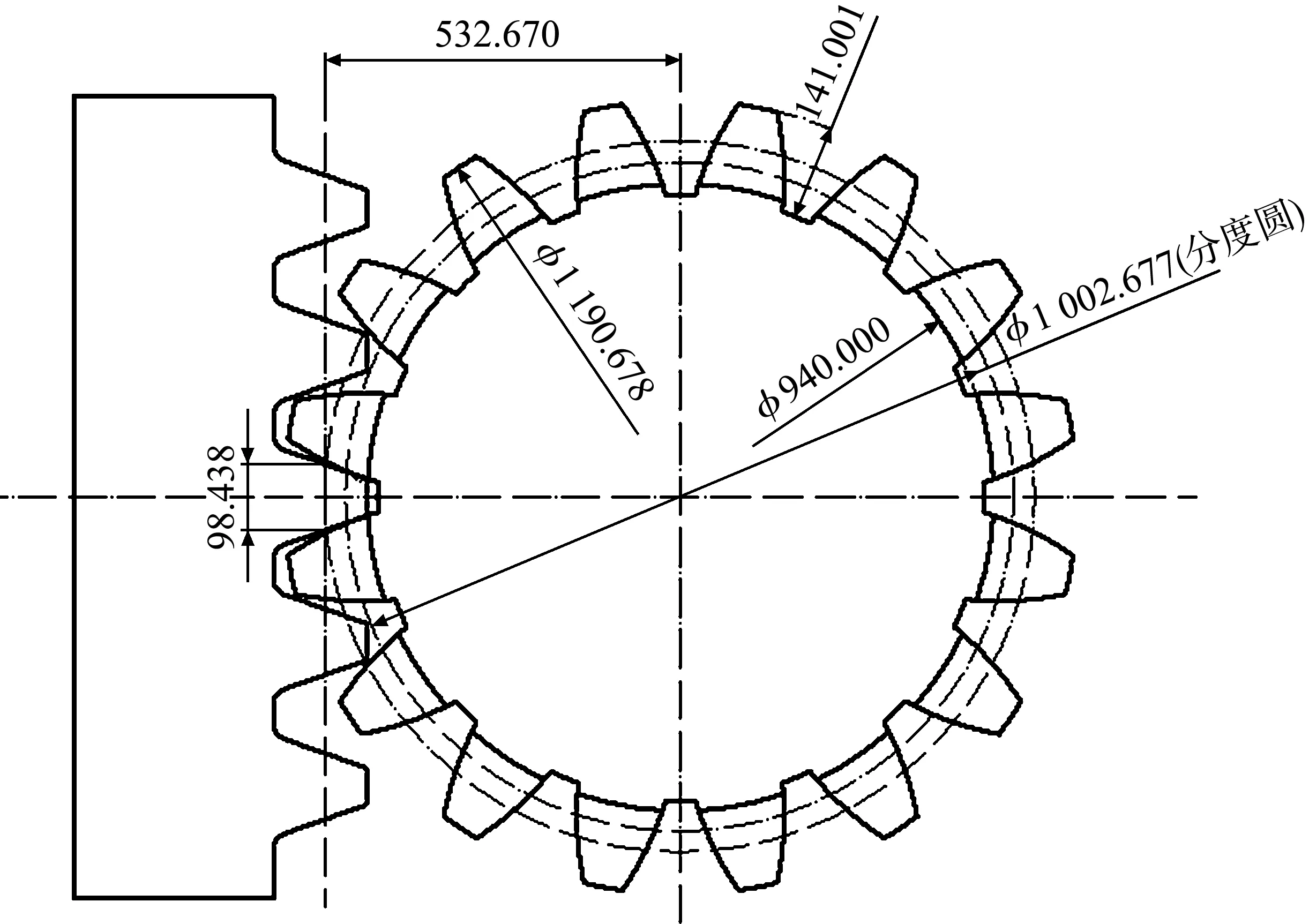
图1 齿轮齿条啮合示意(单位:mm)
1.2 有限元模型建立
根据齿条中夹杂物尺寸、形状、分布特点,为了在有限元软件中模拟夹杂物对齿条应力的影响,基于文献[2-3]对齿条内夹杂物及缺陷描述“夹杂物存在于齿条部分单元中,且夹杂物弹性模量为钢材的0.30~0.75倍,泊松比为0.178~0.306”,因此,本文做如下假设:1)齿条内夹杂物沿齿轮齿条啮合作用线分布,夹杂物设置见图2。2)由于夹杂物存在,且夹杂物与钢基体弹性模量、泊松比不同,通过改变夹杂物的材料常数来模拟夹杂物对齿条接触应力及剪应力的影响。3)对存在夹杂物单元进行更为细小剖分,剖分越接近夹杂物真实尺寸,计算结果越真实有效。夹杂物的尺寸为0.5 mm×0.5 mm×1 mm的立方体。为了在有限元软件中便于施加齿轮的弯矩,齿轮中心设置直径100 mm的圆孔,本文主要研究齿条的应力,齿轮中心开孔对计算结果影响较小可忽略[4-7]。齿轮齿条啮合为线接触,并且随时间推移接触线呈规律变化,为了精确模拟齿轮齿条的相对运动及运动过程产生的应力应变,对两者进行动态接触模拟分析,采用Ansys Workbench中的瞬态分析功能,齿轮齿条三维有限元模型见图3。

图2 齿条内夹杂物分布(单位:mm)
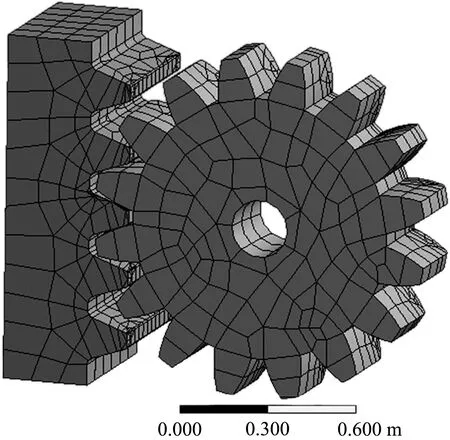
图3 齿轮齿条啮合有限元模型
2 计算结果及分析
2.1 设计的理想工况
齿条设计过程在确定加工及热处理工艺时,未考虑缺陷的工况,为设计的理想工况。根据三峡升船机设计文件,升船机正常运行驱动机构最大工作载荷为1 100 kN,小齿轮等效载荷为932 kN。将升船机在超载工作状态下的小齿轮载荷分为4个工况,工况1:驱动机构载荷超过1 560 kN时,监测和控制系统发出报警,小齿轮等效载荷为1 322 kN;工况2:驱动机构载荷超过1 580 kN时,主拖动系统开始电气制动,至船厢停止升降后,工作制动器和安全制动器先后上闸,小齿轮等效载荷为1 339 kN;工况3:驱动机构载荷达到1 650 kN时,液气弹簧开始动作,小齿轮等效载荷为1 398 kN;工况4:当安全机构螺纹间隙消失时,驱动机构最大事故荷载2 200 kN,此时小齿轮等效载荷为1 864 kN。
2.1.1理论计算
根据《机械设计手册》[8],齿轮齿条接触应力为:
(1)
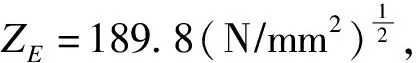
其中螺旋线载荷分布系数KHβ为:
(2)
通过计算得到4种工况下齿轮齿条的接触应力为651.1、655.3、669.6、773.2 MPa。升船机正常运行最大载荷状态下,齿轮齿条接触应力为545.7 MPa。
2.1.2有限元分析计算
齿轮和齿条啮合是复杂的接触问题,且理论计算结果与与齿轮齿条运行的接触应力存在一定误差,因此对上述4种工况进行复核。齿轮材料为18CrNiMo7-6 ME,热处理后踏面硬度为56~61HRC,齿条材料为G35CrNiMo6-6+QT1,热处理后踏面硬度≥520 HV。将4种工况下小齿轮受力转换成扭矩为1 122.7、1 137.1、1 187.5、1 583.3 kN·m。
Ansys Workbench在做接触分析的非线性问题时,若选取整个模型分析,需要较多的单元、节点和内存空间,同时花费大量的求解时间,计算精度也会受到影响。为方便分析,仅建立模型的12进行计算,沿齿轮齿条中心对称XY平面简化模型,设置边界条件时,在对称面上添加“symmetric”约束[9-11]。齿轮齿条基体取弹性模量E=206 GPa,泊松比ν=0.3,齿轮与齿条的面的啮合接触设置为有摩擦约束,摩擦系数为0.3。瞬态分析时给齿轮内孔设置扭矩。计算结果见表2和图4、5。
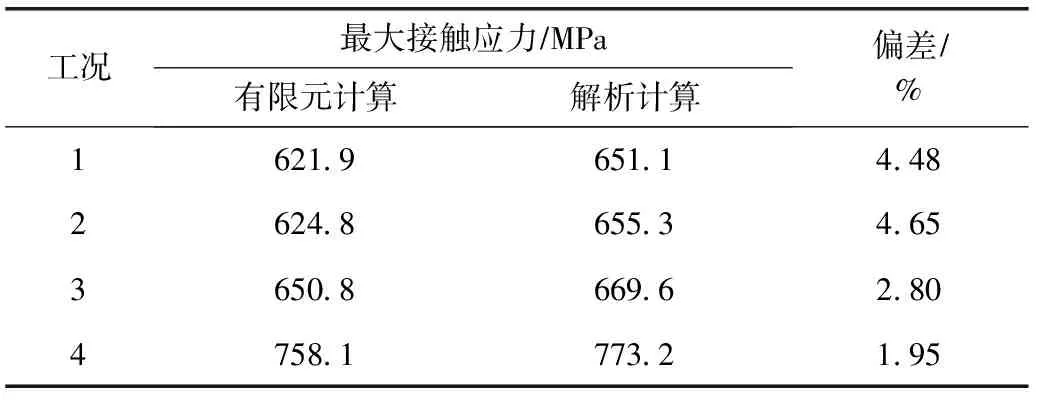
表2 不同工况下齿条最大接触应力计算结果
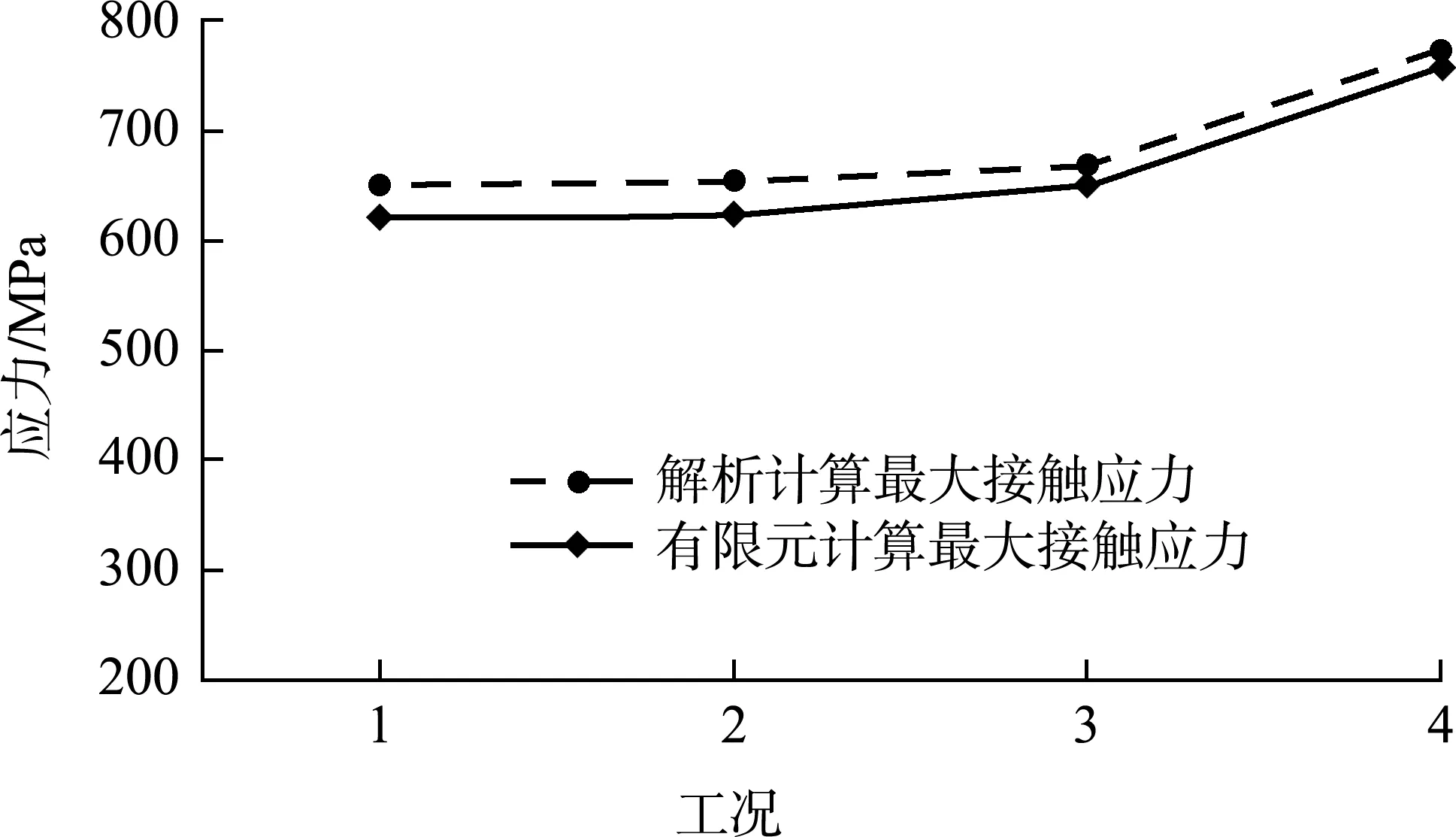
图4 不同算法对齿条最大接触应力影响



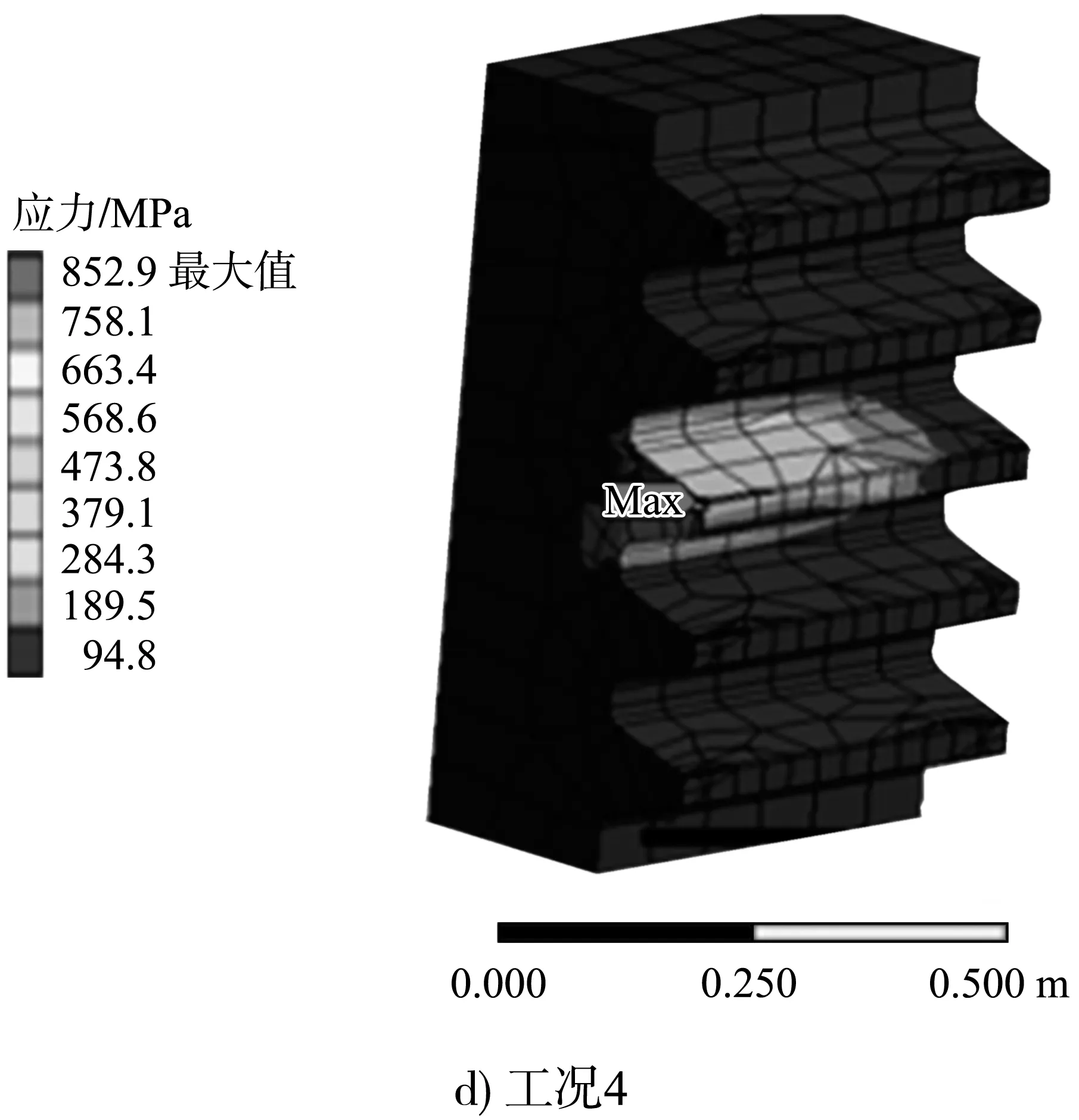
图5 不同工况下齿条接触应力云图
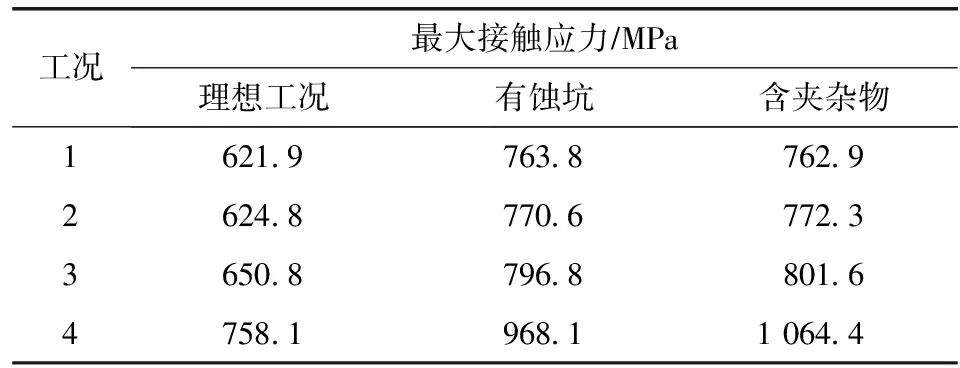
由表2、图4、5可知:1)4种不同载荷工况下齿轮齿条啮合最大接触应力均发生在啮合表面。2)查看图5中工况4齿条最大应力为852.9 MPa,位置并未在啮合处,而是出现在了齿条齿顶内部的单元耦合部位,查看计算结果判定为应力集中点。忽略应力集中点,齿条的最大应力为啮合表面的758.1 MPa。3)不同工况下随着载荷增大,接触应力呈非线性增大趋势。4)有限元计算结果与理论计算的偏差均小于5%,在合理偏差范围之内。
2.2 齿条含夹杂物
2.2.1不同载荷工况下
含夹杂物齿条分析计算时,夹杂物取弹性模量E=300 GPa,泊松比ν=0.2,齿轮与齿条的啮合面、齿顶部缺陷与齿轮面的接触设置为“有摩擦约束”,摩擦系数设置为0.3;其余夹杂物与齿条的接触设置为“固定约束”。夹杂物位置网格划分见图6,计算结果见表3、图7。

图6 齿条夹杂物位置网格划分

表3 含夹杂物不同工况下齿条最大接触应力
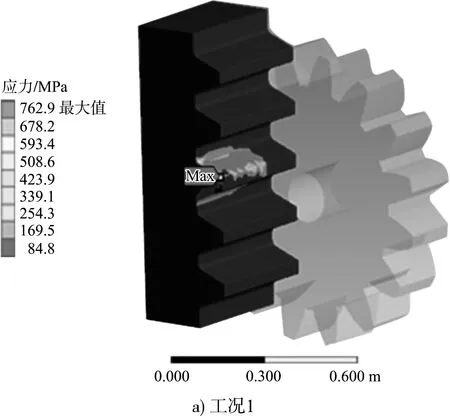
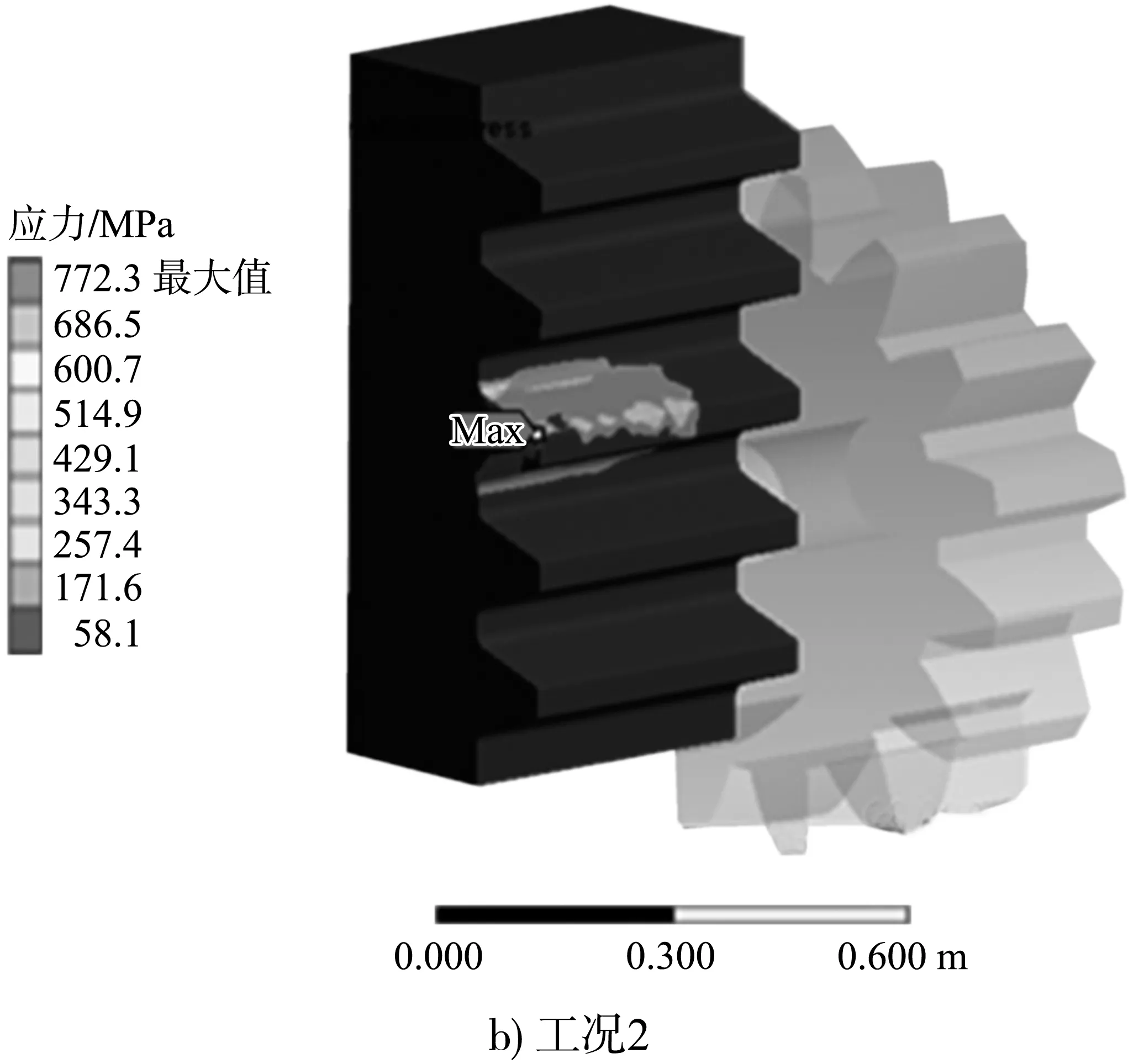
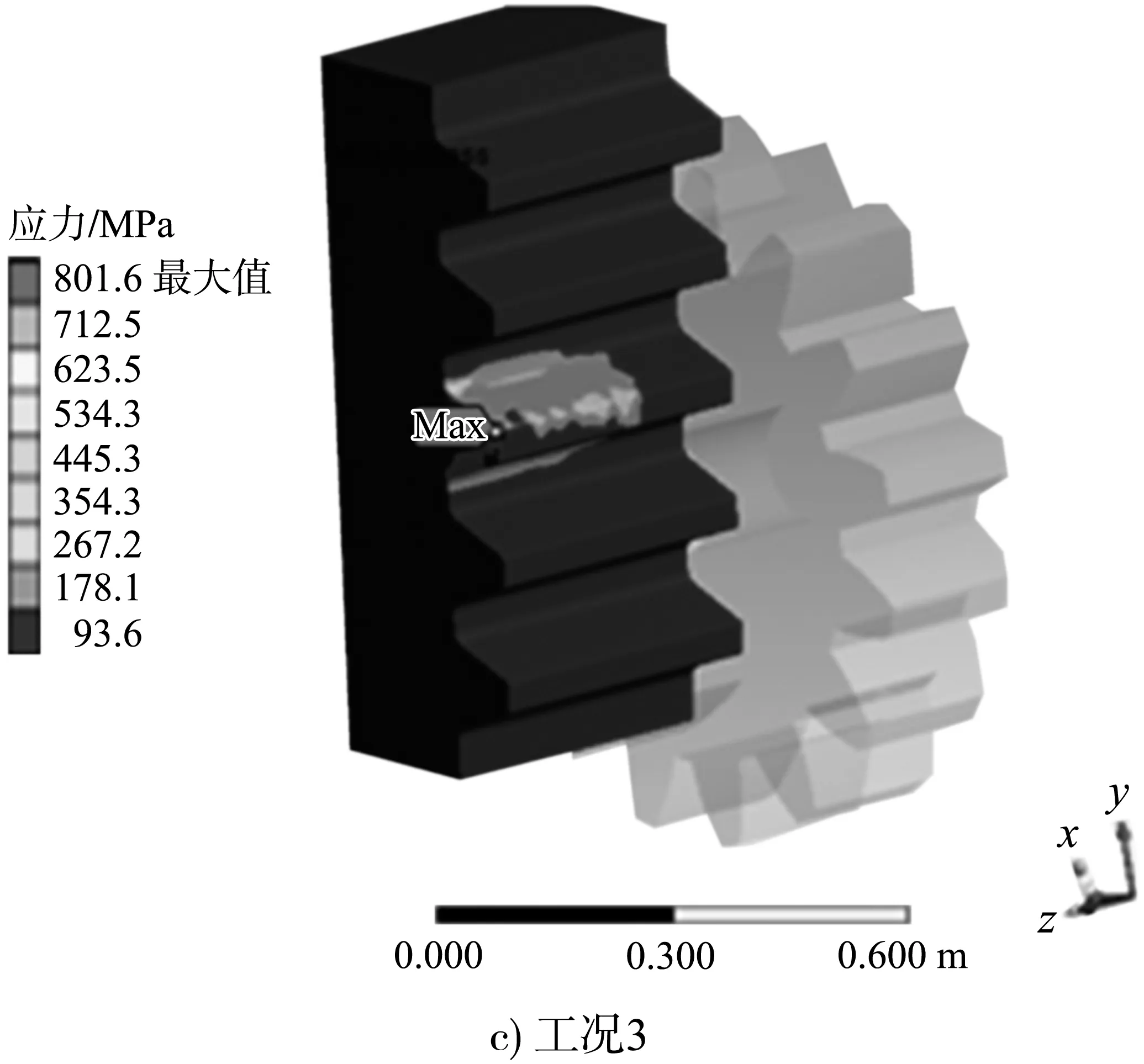
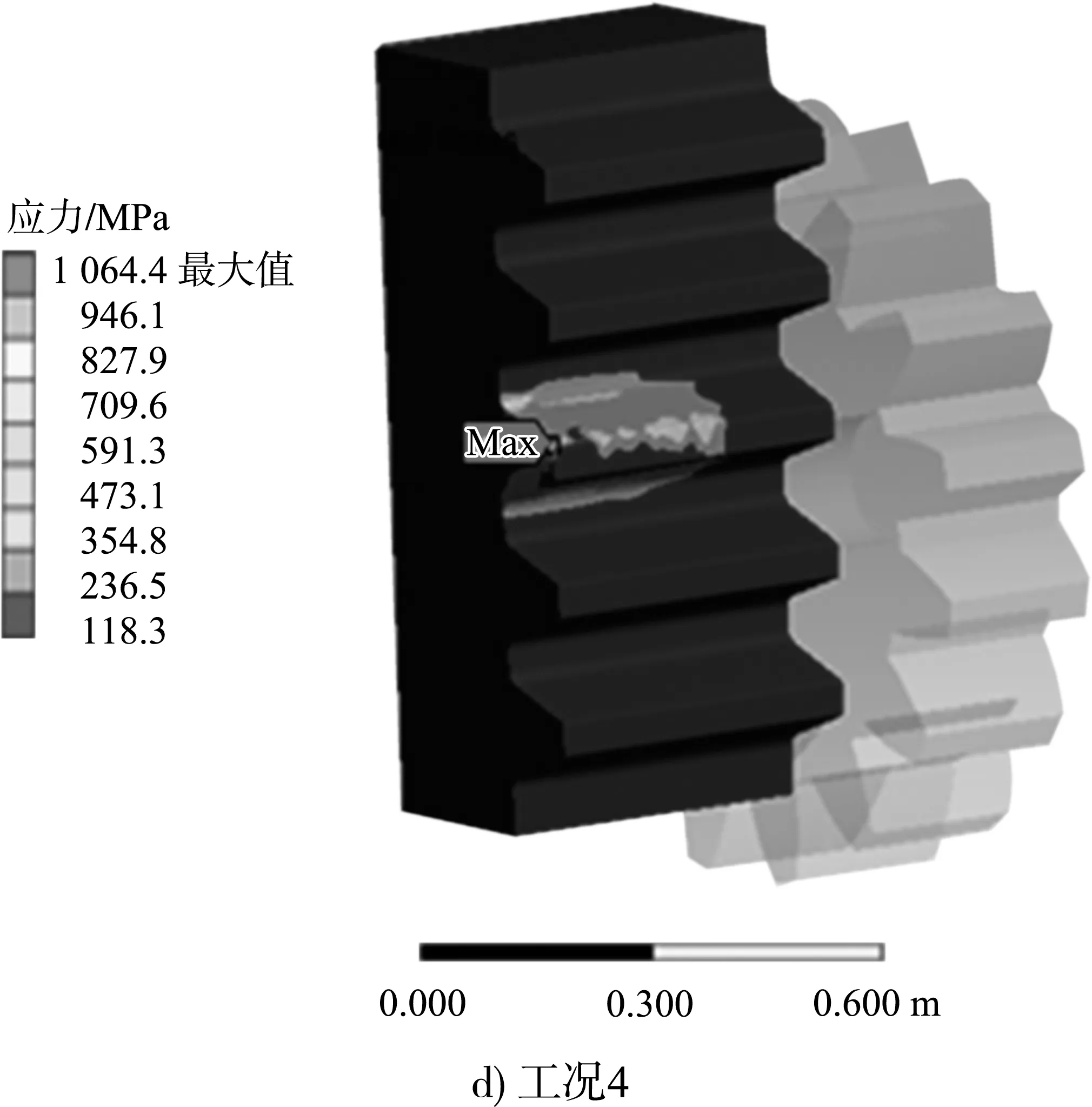
图7 含夹杂物不同工况下齿条接触应力云图
由表3、图7可知:1)齿条含有夹杂物时,啮合作用线位置夹杂物出现较大的应力。2)齿条在设计理想工况和含夹杂物工况下,随着荷载增加,齿轮齿条接触应力均呈非线性增大,在最大事故工况荷载作用下接触应力增幅剧烈,因此,在重载工况下齿条内夹杂物对齿条影响较大。3)在事故工况下,齿条虽不会被破坏,但可能出现不可恢复的形变,齿轮齿条长期运行,在交变应力作用下会发生胶合和齿面接触疲劳,出现安全事故。
2.2.2不同弹性模量工况
齿轮齿条基体弹性模量取E1=206 GPa,用远小于齿条基体弹性模量E2=1 GPa模拟齿条中气孔,对齿条中夹杂物弹性模量再分别取E2=150、206、300、412、620 GPa进行模拟,在最大事故工况4,计算1 864 kN等效荷载作用下齿条的最大接触应力及最大剪应力,结果见表4、图8。

表4 不同弹性模量夹杂物下齿条的最大接触应力和最大剪应力

图8 不同弹性模量夹杂物对齿条应力影响
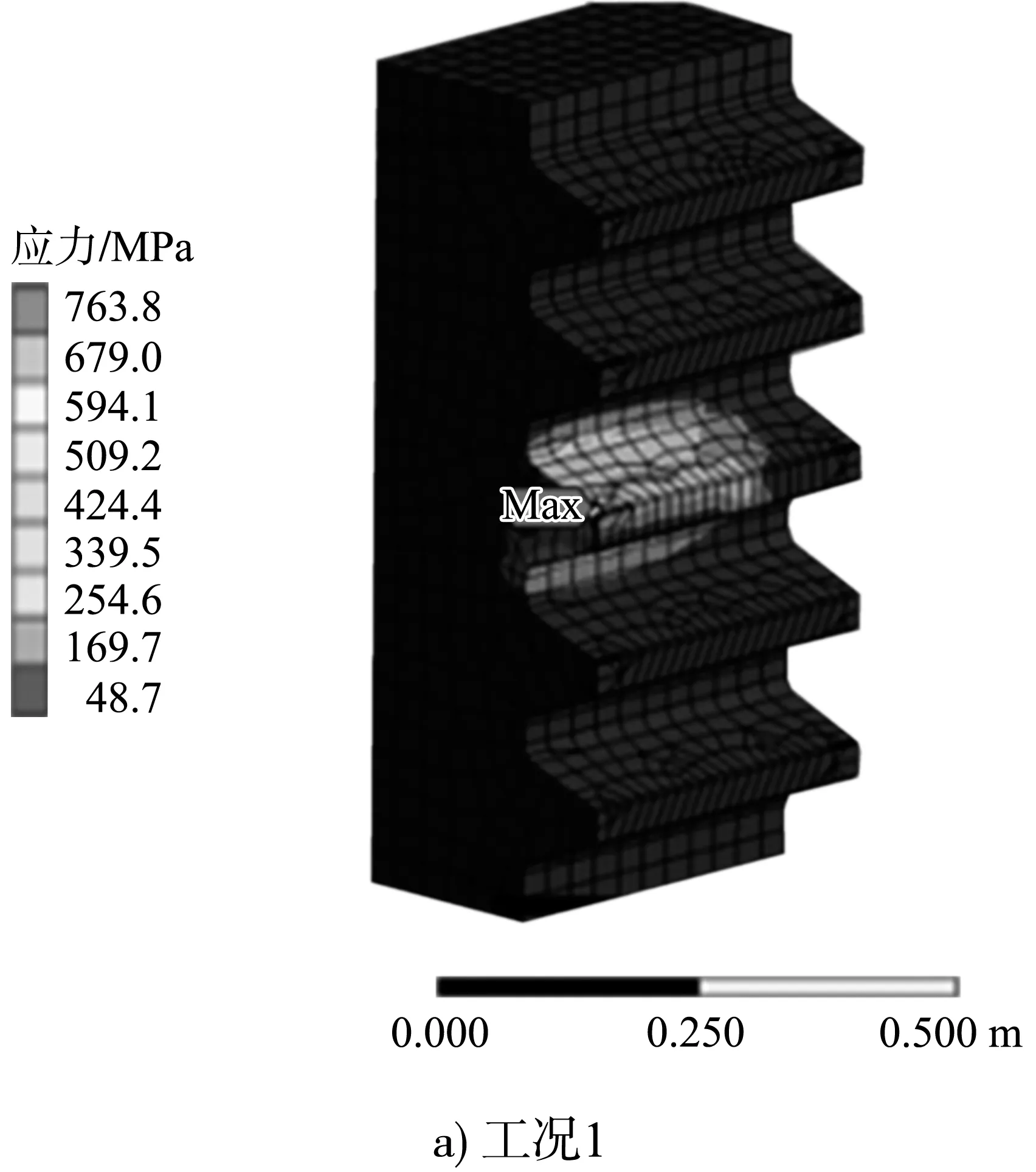
由图8、表4可知:1)当弹性模量E2>E1、E2=E1、E2 2.2.3不同泊松比工况 对齿条内夹杂物泊松比分别取ν2=0.04、0.06、0.09、0.20、0.30,齿条基体泊松比取ν1=0.3,同样在最大事故工况4,计算1 864 kN等效荷载作用下的齿轮齿条的最大接触应力及最大剪应力,结果见表5、图9。 表5 不同泊松比夹杂物齿条的最大接触应力和最大剪应力 图9 不同泊松比夹杂物对齿条应力影响 由图9、表5可知:1)当泊松比ν2<ν1时,齿条的最大接触应力与最大剪应力随着泊松比的增大而减小,成反比例关系,最大接触应力与最大剪应力均发生在夹杂物齿条基体交界位置附近。2)当泊松比ν2=ν1(即不含夹杂物)时,齿条最大接触应力与最大剪应力发生在b1点,即齿轮齿条啮合作用线上。3)有夹杂物区域齿条最大接触应力和最大剪应力均大于ν2=ν1时的最大接触应力与最大剪应力,而不在啮合作用线上的c1、c2、c3点夹杂物的应力相对较小,表明齿轮齿条啮合作用线上的夹杂物对齿条应力影响较大,而非啮合线的夹杂物对齿条应力影响较小。 在设计的理想工况模型的基础上,建立蚀坑的缺陷模型,缺陷为0.5 mm×0.5 mm×1 mm的立方体,沿啮合方向和齿厚方向的分布,与夹杂物分布相同。模型分析时,齿轮与齿条的啮合面的接触设置为“有摩擦约束”,摩擦系数设置为0.3。计算结果见表6和图11、12。 表6 齿面蚀坑不同工况下齿条的最大接触应力 图10 齿面蚀坑不同工况下齿条接触应力云图 图11 齿面蚀坑对齿条最大接触应力的影响 由表6和图10、11可知:1)齿条表面有蚀坑时,啮合作用线位置蚀坑出现较大的应力。2)齿面有蚀坑工况下,随着荷载增加,齿条接触应力均呈非线性增大,在最大事故工况荷载作用下接触应力增幅剧烈,因此,在重载工况下齿条蚀坑对齿条应力影响较大。3)在齿条表面有蚀坑时,比设计理想工况时应力增大22.8%、23.3%、22.4%和27.7%,与齿条含有夹杂物相比,在重载条件下,夹杂物比蚀坑更容易引起齿条的应力集中。 1)采用Ansys Workbench有限元分析软件模拟计算了齿条在含夹杂物、蚀坑等缺陷应力场分布情况,在齿条内缺陷数量和分布特点未知情况下,假设一种夹杂物及蚀坑的数目及分布策略,可有效分析缺陷对齿条受力的影响,夹杂物和蚀坑使得齿轮齿条啮合过程最大接触应力及最大剪应力位置发生变化。 2)该方法对齿条热处理过程控制齿面及齿顶淬硬层达到硬化深度、减少夹杂物对齿条的影响及齿轮齿条维护保养等提供理论依据。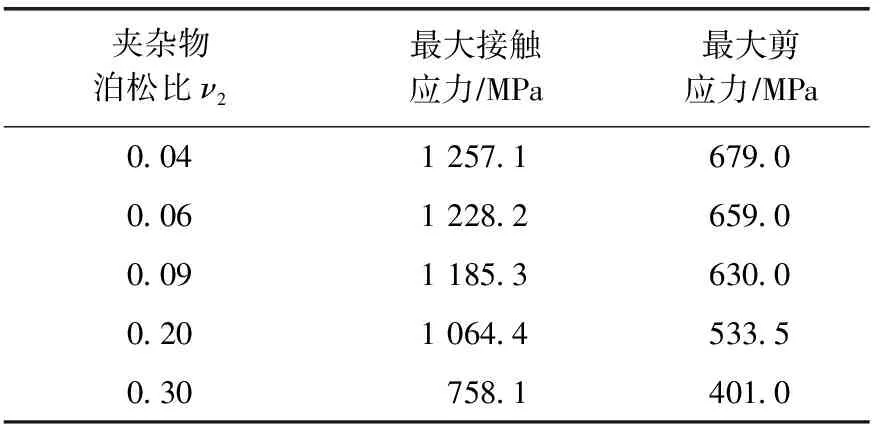

2.3 啮合表面有蚀坑




3 结论
