基于精细有限元法的直升机尾传动系统振动特性研究*

2022-05-20李德玉胡玉梅杨广勇

机械研究与应用 2022年2期

李德玉，胡玉梅，杨广勇，陈鹏

(1.中国直升机设计研究所,江西景德镇 333000；2.机械传动国家重点实验室，重庆大学,重庆 400044)

0 引言

直升机尾传动系统，主要负责平衡直升机运转时主旋翼的反扭矩，关系到直升机的航向操纵，一旦存在故障，尾桨将无法正常工作，极易导致飞行事故[1]。而振动问题是直升机尾传动系统故障里最核心的问题，它不仅会导致零件的磨损，加速结构件的疲劳失效，更会导致高速运转的直升机尾传动轴的动力失稳，这在广泛应用了超临界轴的高速直升机上尤为突出[2]。所以对直升机尾传动系统振动特性及其影响因素进行研究，对提高直升机飞行的安全性、稳定性具有重要意义。国内，梅庆[3]从转子动力学理论出发，研究了直升机尾传动轴系的临界转速、稳态不平衡响应、瞬态突加不平衡响应规律。许兆堂[4]建立简化的直升机尾传动系统扭转动力学方程，研究了直升机尾传动系扭转振动的求解方法以及频响函数的变化幅值的测试方法。国外，Hetheringto[5]通过实验的方法研究了超临界复合材料传动轴在外部阻尼作用下的动态特性。Ananthan[6]采用数学解析法，系统研究了不同的空间机动动作对直升机传动轴的振动特性及稳定性的影响。Li Ping[7]等建立了直升机传动系统的动力学模型，通过对动力学模型设置不同的初始计算条件，对直升机传动系统动力学特性进行相应的研究。

直升机尾传动系统的振动来源复杂，齿轮啮合振动激励、传动花键磨损、膜片联轴器膜片刚度、轴承游隙，这些对直升机尾传动系统的振动特性都有着重要影响[8-10]。以往对于直升机尾传动系统的研究主要集中在尾传动系统的静强度设计、尾传动轴系的弯扭振动、临界转速的计算等方面[11-13]，但很少考虑实际尾传动系统里几何、材料、接触等复杂等非线性因素的影响，对尾传动系统整体进行瞬态动力学的振动特性研究也比较少见。由于针对直升机尾传动系统振动特性的研究，试验成本高，装置复杂，部分数据提取困难。笔者供了一种新的研究思路。采用精细有限元方法建立含有完整的尾传动系统零件与复杂几何、材料、接触等非线性因素的计算模型并进行验证；在此基础上研究整个尾传系统振动特性，为直升机尾传动系统的振动分析与优化设计提供参考。

1 模型精细化建立与验证

直升机尾传动系统主要由主减速器锥齿轮、中间减速器锥齿轮、膜片联轴器、花键等重要部件组成，如下图1所示。本节主要建立了考虑复杂几何、材料、接触等非线性因素的尾传动系统计算模型，并对关键膜片联轴器、花键、锥齿轮的准确性进行验证，为后续整个尾传动系统瞬态振动特性分析做铺垫。

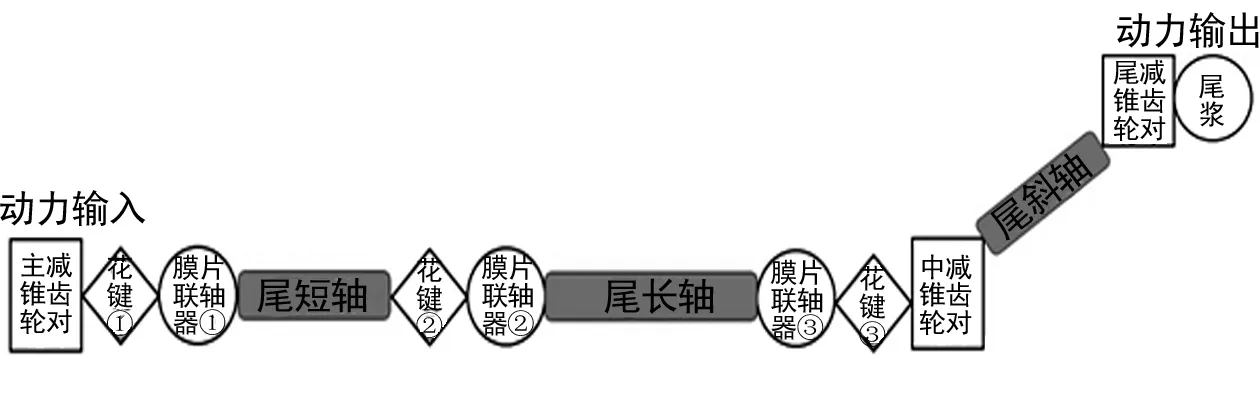
图1 直升机尾传动系统组成示意图

1.1 膜片联轴器模型建立及其准确性验证

膜片联轴器是一种广泛应用在各种大功率轴系间传动的金属挠性联轴器，依靠联轴器中间金属膜片的弹性变形，补偿所联接两轴由于制造、安装误差以及温升、受载变形导致的相对位移，从而保证轴系设备的安全可靠运行[14]。通常情况下膜片联轴器许用径向位移、轴向位移、扭转、角位移补偿原理示意图如图2所示。

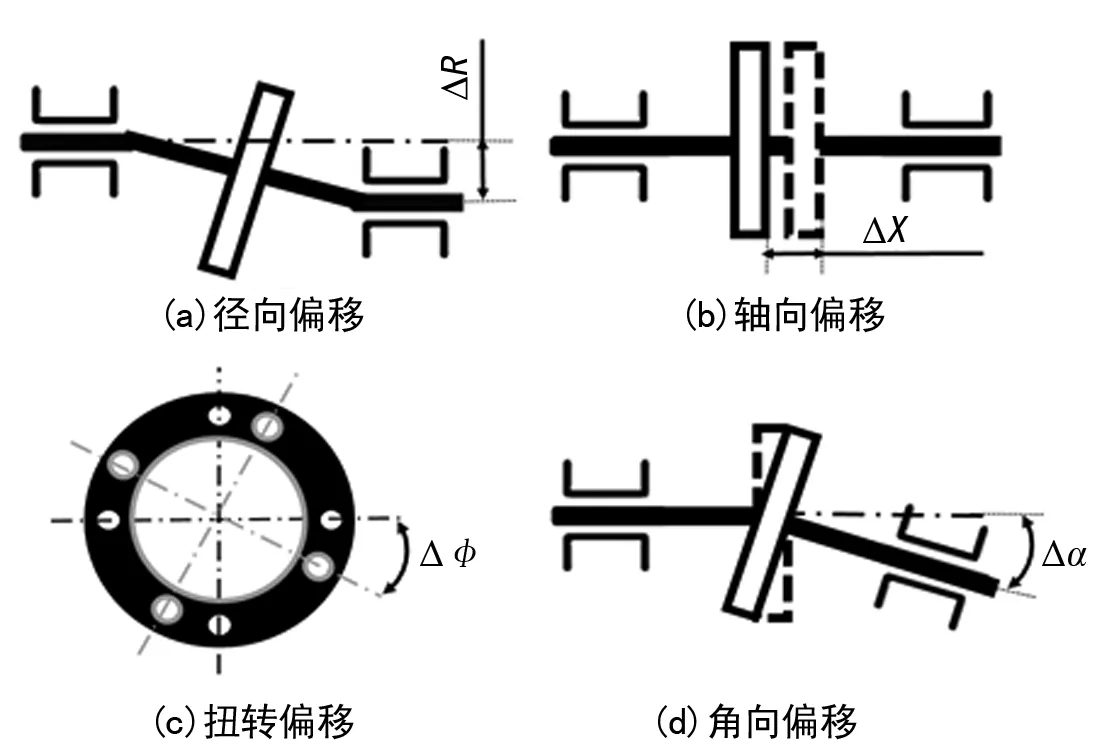
图2 膜片联轴器补偿位移原理示意图

建立膜片联轴器三维模型，使用前处理软件将几何模型离散为有限元网格，接着设置膜片联轴器的接触边界条件。接触类型使用的是自动面面接触。模型边界条件设置部分示意图如图3所示。

图3 膜片联轴器有限元模型边界条件

膜片联轴器的各向刚度值计算公式如下：

使用LS-DYNA求解器仿真的结果如图4所示。

图4 膜片联轴器仿真计算结果

综合以上仿真计算的结果，可以得出膜片联轴器各向刚度的仿真值，将其与膜片联轴器的产品实验值进行对比，即可验证仿真结果的准确性，对比结果如下表1所列。

表1 联轴器刚度仿真值与实验值对比

从表可以观察出：使用精细有限元法计算的膜片联轴器各向刚度仿真值与产品试验值数值较为接近，都不超过10%，这说明仿真计算的膜片联轴器各向刚度较为准确。

1.2 花键模型建立及其准确性验证

文中所涉及到的直升机尾传花键为渐开线花键，为确保模型确保最接近实际的齿面形貌，使用KISSsoft直接建立了考虑齿侧间隙、修形等重要模型参数的尾传花键模型，然后将其划分网格，将内外花键三维模型离散化为六面体网格。对其施加边界条件，建立接触，施加转速转矩，根据传力路径，外花键内孔面施加转速V，内花键外轴面施加负载力矩T[15]。边界条件施加如图5所示。

图5 渐开线花键有限元模型边界条件加载

根据GB/T 17855-1999可以计算出直升机尾传花键运行工况下的花键齿接触面上的压应力均值σ，公式如下：

提取仿真结果中的尾传花键齿面平均压应力σ，进而方便与由理论公式对比，验证仿真的准确性。使用LS-PrePost，可以提取该尾传渐开线花键齿面在黑色虚线矩形区域平均压应力σ值，如图6所示。

图6 仿真中尾传花键齿平均压应力

结果显示花键接触齿面上的压应力均值在41.7 MPa左右。理论计算的结果为45.1 MPa，仿真值比理论值小7.6%，花键的有限元模型是相对准确可靠的。

1.3 锥齿轮模型建立及其准确性验证

同上，使用了KISSsoft建立考虑了齿侧间隙与齿顶倒圆角参数的高度贴近实际工况下的锥齿轮三维模型，离散化为六面体网格。对其施加边界条件，根据实际传力路径，大锥齿轮施加转速V，小锥齿轮施加负载力矩T。边界条件施加如图7所示。

图7 锥齿轮有限元模型边界条件加载

齿轮接触力在一定程度上可以直接反映齿轮传动的运转情况，可以使用理论公式计算出齿轮的各向接触力：圆周力Ft1，径向力Fr1，轴向力Fx1：

=-7 546.9 N

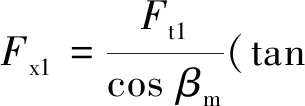
=7 424.8 N

然后提取准静态下仿真值以及瞬态稳定条件下的值与理论值进行对比，验证仿真结果。仿真提取的齿轮接触力如图8所示。

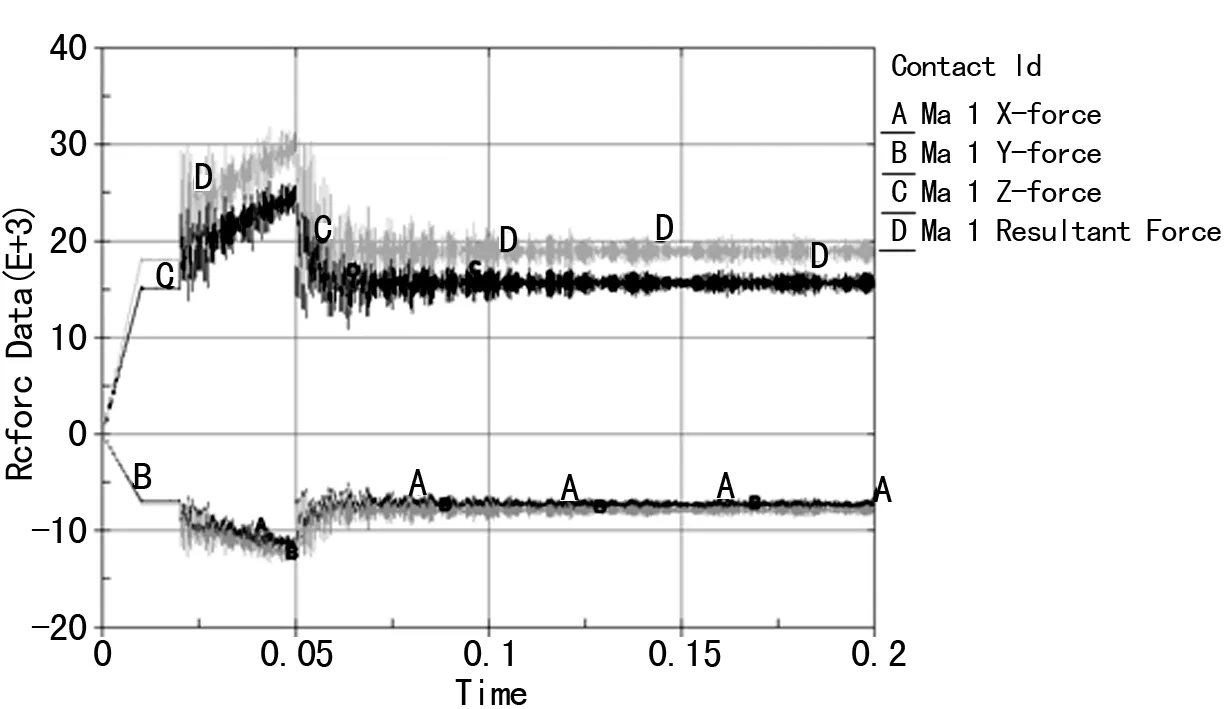
图8 锥齿轮接触力

表2 锥齿轮接触力仿真值与实验值对比 /N

由表2可以得出，从合力值可以观察得到准静态仿真计算值与理论值偏差为0.04%，这说明了锥齿轮模型的正确性以及仿真的可靠性；同时观察锥齿轮对瞬态稳定啮合运动过程中，锥齿轮的三向力的合力比理论值偏大(4.2%)，这是建模考虑实际施加的阻尼效果导致的。总体分析准静态以及瞬态计算是比较准确的。

2 尾传动系统振动特性分析

利用前面建立并验证的模型，建立尾传系统整体瞬态动力学有限元模型在此基础上计算分析直升机尾传动系统运行工况下的应力分布及振动特性。

2.1 尾传动系统边界条件设置

将尾传动系统的主减锥齿轮、中减锥齿轮、尾减速器、传动花键、膜片联轴器、尾轴轴承、阻尼圈、尾桨装配在一起，组成直升机整体尾传动系统模型。实际约束及载荷边界条件施加如下：对尾传动系统模型中的轴承的外圈及减振阻尼圈施加固定约束，对主动轴(主减大锥齿轮轴)施加的转速V，从动轴(尾桨轴)施加负载阻力力矩T。具体的约束以及转速、负载转矩施加情况如图9所示。

图9 直升机尾传动系统边界条件设置

2.2 尾传动系统瞬态动力学应力分布情况

提取模型瞬态计算结果，得到尾传动系统的应力分布情况，由于尾传动轴(短轴与长轴)是细长轴，是振动分析的重点关注部位，提取尾传轴各个位置编号所对应的应力云图如图10所示，可以方便的了解实际瞬态运行工况下的尾传系统各个部位应力大小以及位置分布情况。

图10 尾传长轴提取位置与应力云图

将提取结果绘制各部位的应力随时间变化曲线，可得出尾传动轴过临界转速加载时，尾传短轴应力最大500 MPa高于相对长轴350 MPa，稳定阶段，两者相差不大，尾传短轴与长轴应力值相对加载阶段也比较平稳。如图11所示。

2.3 尾传动系统尾传轴局部振动情况

在了解应力分布情况后，进一步提取尾传动短轴与长轴的轴线上的对应位置节点1、2、3、4、5、6振动情况，主要包含沿着轴向窜动情况，即轴向位移振动随时间的变化历程曲线如图12所示，以及沿着径向跳动情况，即径向位移振动随时间的变化历程曲线如图13所示。

图11 尾传短轴与长轴提取应力随时间变化曲线

图12 节点轴向位移振动时间历程曲线

图13 节点径向位移振动时间历程曲线

综合以上数据，可以得出尾传轴在瞬态运行稳定工况下的尾传轴的振动情况规律：

(1)轴向振动情况。从传动轴节点轴向位移振动时间历程曲线上可以观察出，尾传短轴节点1、2、3曲线几乎重合，长轴节点4、5、6曲线也是几乎重合，这说明尾传轴没有发生较大的弯曲，轴向各轴上运动一致，而短轴、长轴波动曲线的波形相近，但相位有一定差别，推测这可能受膜片联轴器的轴向刚度影响；而波动曲线的峰值，反映了尾传轴轴向相对初始安装位置的位移运动情况，从图12可以发现短轴稳定状态下位移最大值要稍大大于尾传长轴位移最大值，由轴的移动所导致的尾传短轴上的花键错位必定大于尾传长轴，短轴上的花键运转时的配合情况要差于长轴上的花键；波动曲线的峰峰值反映的是尾传轴运行时的瞬时轴向窜动情况，这直接关系到轴所连接的花键的轴向相对刮擦运动，从峰峰值上观察，尾传短轴峰峰值要远大于为传长轴峰峰值，几乎是其2倍，故尾传短轴上的花键轴向刮擦要大于长轴。

(2)径向振动情况。从传动轴节点径向位移振动时间历程曲线上可以观察出，尾传短轴径向振动最为剧烈最大接近1.2 mm，接近尾传长轴振动量的2倍，且短轴三个节点径向振动差异较大；尾传长轴上三个节点径向振动量则比较接近，值0.5 mm。通过观察各传动轴径向振动情况，可看出瞬态运行时尾传短轴的径向跳动要大于尾传长轴，同时各轴的中间位置跳动大于两边。

综上无论是轴向振动还是径向振动，尾传短轴的运行工况都要较尾传长轴更为恶劣，应加强对尾传短轴及其附属零配件(如花键、轴承、阻尼圈)的优化设计与监测维护，防止零件损坏。