斜齿轮实体模型的精确创建

赵 春

(内蒙古机电职业技术学院，内蒙古 呼和浩特 010070)

1 渐开线及其基本性质

如图1所示，渐开线齿轮轮齿两侧的工作齿廓是内两段对称的渐开线所组成。渐开线的形成过程如图2所示，当一直线L沿某一半径为rb的圆周作纯滚动，该直线从位置I顺时针方向滚动到位置II时，直线上任一点K所形成的轨迹众AK就是该圆的渐开线。

图1 渐开线的形成

图2 渐开线齿廓的形成

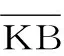
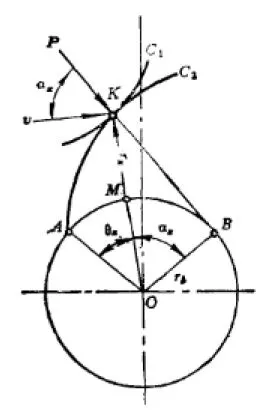
图3 渐开线齿廓的压力角

渐开线的数学方程式，为了对渐开线齿轮啮合传动的一些参数进行计算，渐开线的数学方程式最常用的是极坐标方程式由上图可知，rx为渐开线上任意一点的向径，θx为渐开线上任意一点的渐开角。

任意一点的向径为:

(1)

渐开线上任意一点的渐开角θx为:

θx=tanαx-αx

(2)

(2)式中的tanαx、θx和αx均以弧度表示。

由上式可知，渐开线θx是随压力角αx的大小变化的，只要知道渐开线上各点的压力角αx，则可求出各点的渐开角θx。因此称的渐开角θx为压力角αx的渐开线函数，用invαx表示invαx=θx。

渐开线曲线方程的建立，时刻t时，AB段线段在坐标系2中的曲线族参数方程为：

(3)

(4)

消去θ得到:

(5)

在方程(3～5)两边对α求偏导得到：

(6)

联立式(3～5)，式(3～6)可得：

(7)

则可得，渐开线的极坐标方程为：

(8)

斜齿轮Pro/E内笛卡尔坐标系下的渐开线方程：

r=DB/2

theta=t×45

x=r×cos(theta)+r×sin(theta)×theta×pi/180

y=r×sin(theta)-r×cos(theta)×theta×pi/180

z=0

2 过渡曲线方程

齿根过渡曲线形状分别由刀具与齿坯的相对运动关系和刀具顶部的刃形决定，齿条形刀具加工出来的齿轮的过渡曲线是延伸渐开线的等距曲线，而由齿轮型刀具则为延伸外摆线的等距曲线，如图3～图4所示。

I、II两段为延伸渐开线的等距曲线III段为齿轮的根圆圆弧

I段为延伸渐开线的等距曲线

对于第一种过渡曲线，其参数具有以下关系：

xc=ha*m+c*m-ρ0

(9)

(10)

(11)

刀具齿廓如图3～图5所示，其参数具有以下关系：

xc=ha*m+c*m-ρ0

(12)

(13)

(14)

在以上刀具参数关系式中：

xc—刀顶圆角圆心距中线的距离；

yc—刀顶圆角圆心距刀具刀槽中心的距离；

ρ0—刀顶圆角半径。

2.1 过渡曲线方程的建立

BC段圆弧在展成运动过程中形成的曲线族在坐标系2中的参数方程：

(15)

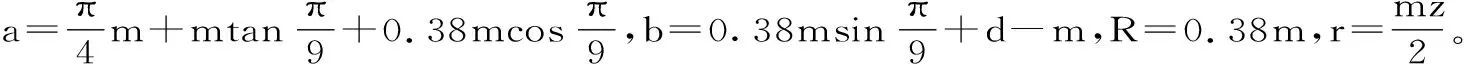
消去θ，可得：

(x-(a-rα)cosα-bsinα)2+(y-(rα-a)sinα-bcosα)2=R2

(16)

方程两边对α求偏导，可得：

(x-l1)l2+(y-l3)l4=0

(17)

其中，l1=(a-rα)cosα+bsinα,

l2=(b-r)cosα+(rα-a)sinα,

l3=(rα-a)sinα+bcosα,

l4=(r-b)sinα+(rα-a)cosα

在消去θ的过程中引入了多余的根，所以上述4组解中有3组是不符合要求的，通过实际作图判断，可以得到合理的一组解，作为过渡曲线在坐标系2中的参数方程。联立上述两个方程求解可得到:

(18)

建立如图3～图5所示的齿条刀具和齿轮坯的坐标系。曲线ABC为齿条刀具齿廓，其中AB段为直线，BC段位圆弧。d为齿条刀具节线与齿轮轮坯中心间的距离。设齿轮的变位系数为x，则d=m(z/2+x)。坐标系1与齿条刀具固连，坐标系2与齿轮坯固连。为了求取齿轮轮齿齿廓曲线方程，可将展成运动简化成如下运动：齿条刀具沿x1方向以速度v平动，齿轮坯绕自身原点以角速度w转动。v与w之间满足：

(19)

图5 刀具齿轮坯坐标系

若以齿轮坯坐标系为参考坐标系，则展成运动可看成齿条刀具绕着坐标系2的原点转动，同时,沿着切线方向平动。在运动过程中，AB线段曲线族的包络线就是齿轮轮齿的渐开线部分，BC段圆弧曲线族的包络线就是过渡线部分。

初始状态时，AB段曲线在坐标系1中的参数方程为：

(20)

-m≤θ

BC段曲线在坐标系1中的参数方程为：

(21)

2.2 渐开线斜齿轮精确建模

斜齿轮的建模分析：

2.2.1 创建齿轮的基本圆。首先用草绘曲线的方法，以任意直径绘制4个同心圆，如图6所示，通过参数之间的关系来控制圆的大小。

图6 创建齿轮的基本圆

2.2.2 创建并镜像渐开线。用定义曲线方程来生成渐开线齿廓的方法，如图7所示，创建精确的渐开线。然后镜像已创建的渐开线，用关系式来控制镜像平面之间的角度。

图7 创建并镜像渐开线

2.2.3 拉伸形成实体。通过拉伸创建齿根圆实体和齿轮的首个齿形，如图8所示。

图8 拉伸形成实体

2.2.4 阵列轮齿。对创建的轮齿进行阵列，如图9所示，完成齿轮的基本外形，同样需要加入关系式来控制齿轮的齿数以及其他参数。

图9 阵列轮齿

2.2.5 阵列轮齿。创建齿轮的轮轴、倒角、端面孔等细节特征，最终齿轮轴实体如图10所示。

图10 齿轮轴实体

2.2.6 斜齿轮副装配。根据齿轮副中心距设置装配轴线，以销钉连接的装配方式，选择轴对齐保证与齿轮中心轴线重合，以轴端面为对齐平面设置端面偏距，完成齿轮副的装配，在应用程序里设置齿轮副定义。装配体效果如图11所示。

图11 斜齿轮装配体