基于多参数耦合的圆柱滚子轴承润滑分析*

2022-05-19戴铭阳陶友瑞

润滑与密封 2022年3期

戴铭阳陶友瑞

(1.河北工业大学机械工程学院天津 300401；2.河北工业大学电气设备可靠性与智能化国家重点实验室天津 300401)

圆柱滚子轴承是最常见的滚动轴承类型，广泛应用于旋转机械系统中，其中滚子在受载区和非受载区交替运行。常见的磨损和失效是由于滚子进入加载区从而使接触界面润滑失效造成的。因此，了解接触区的润滑状态有助于提高圆柱滚子轴承的可靠性。CHANG等[1]基于弹流润滑理论研究了轴承稳态运行时的载荷分布和轴承的滑动特性。CAO、LI等[2-3]研究了基于弹流润滑的圆柱滚子轴承稳态动态特性。贾志博和邱明[4]建立了高速轻载圆柱滚子轴承的动力学方程。CAO等[5]结合弹流润滑研究了最大载荷滚子和内滚道加速过程的润滑性能。ZHANG等[6]提出了有限线接触条件下圆柱滚子型线的数值计算模型，分析了凸度对油膜压力分布的影响。华同曙等[7]通过线接触光弹流实验对滚子轴承进行润滑研究,实验发现在接触区内，呈现明显的马蹄形弹流特征，滚子端部出现闭合效应，因此对于滚子的凸度设计是十分必要的。

圆柱滚子的弹性流体动力润滑研究比较成熟,一些研究人员很早就开始在弹流润滑的基础上研究油膜厚度。早在20世纪60年代，DOWSON和HIGGINSON[8]就提出了考虑负载、速度和材料参数对膜厚影响的最小膜厚方程(D-H方程)。该方程在实践中得到了广泛的应用。GELINCK和SCHIPPER[9]推导了粗糙表面接触压力的曲线拟合方程，然后利用MOES[10]提出的膜厚方程得到膜厚和粗糙度压力的表达式。随后，越来越多的研究人员关注表面粗糙度对油膜厚度的影响[11-14]。MASJEDI和KHONSARI[15]在考虑表面粗糙度和硬度的D-H方程的基础上推导了新的膜厚方程,通过大量的仿真结果回归分析使最小油膜厚度方程更真实地反映实际润滑情况。

在润滑过程中，各种因素会同时影响轴承的润滑状态，固体颗粒就是其中之一。而固体颗粒与润滑剂形成了微极流体，由于流体中含有悬浮的随机取向的固体微粒，在运动过程中呈现出许多有别于牛顿流体的特性，影响着流体润滑性能，因而越来越引起人们的关注。XU等[16]研究了固体颗粒对等温弹流润滑接触的影响，李娜娜等[17]对含固体颗粒的轴承润滑问题进行了分析研究，分析结果表明，沿油膜厚度方向分布的固体颗粒越多，对润滑油流动的阻碍越强，对油膜压力和油膜流动的影响越大。上述研究中仅考虑某单一因素对润滑的影响，这与实际工况的复杂程度差别较大。

本文作者结合轴承动力学，考虑表面粗糙度、微极流体效应及滚子修形的多尺度参数的耦合影响，探讨圆柱滚子复杂润滑模型的建立及润滑分析。

1 轴承动力学模型

1.1 轴承运动分析

圆柱滚子轴承原理如图1所示。轴承的外圈是固定的，内圈随轴旋转。图中：Ri为内圈接触点的圆弧半径；Rm为滚子的圆心半径；Ro为外圈接触点的圆弧半径；ω表示轴承内圈滚道角速度；ωc为保持器角速度；ωj表示滚子的转速；径向力W通过轴作用在轴承上。

根据图1，可得轴承滚子与内外圈相对滑动速度为

Vij=(Rm-Rr)(ω-ωc)-Rrωj

(1)

Voj=(Rm+Rr)ωc-Rrωj

(2)

滚子与内外圈之间的卷吸速度为

(3)

(4)

式中：下标i和o表示与内圈和外圈相关的量;下标j表示滚子的位置，如图1所示，最底下的为0号滚子，沿顺时针编号依次增加。

将上述参数量纲一化可得：

(5)

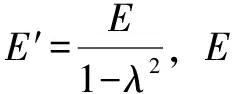
1.2 滚子受力分析

根据图2可得轴承径向载荷平衡方程为

W=Qi0+2∑Qijcosφj

(6)

式中：Qi0为0号滚子与内滚道之间的相互作用力，即最大承载滚子所受的接触力；Qij为j号滚子与内滚道之间的接触力；φj表示第j号滚子的相位角。

变形协调方程如下：

(7)

(8)

(9)

(10)

式中：δc为轴承间隙和接触变形引起的中心位移；uc代表轴承径向游隙；δij和δoj分别表示内圈和外圈的接触变形；l为滚子的长度；m为单个滚子质量。

流体动压力表达式[18]为

(11)

(12)

当轴承运转时，滚子由滚子与滚道之间的摩擦力驱动。量纲一摩擦力(或牵引力)[19]为

(13)

(14)

(15)

(16)

(17)

(18)

1.3 动力学模型

在空载区，由于离心力滚子压在外滚道上，可以认为滚子相对于外滚道的滑动速度为0，则空载区滚子的旋转速度为

(19)

式中：下标u表示与无载荷区相关的量。

空载区各滚子在滚动方向上的力平衡方程为

(20)

(21)

在滚子受载区，假设保持架对每个滚子的力都相等，则轴承匀速转动时，根据受力平衡可得：

(22)

式中：nu为空载区的滚子个数；Z为滚子总个数。

对于受载最大的滚子，由图2可得滚子在滚动方向上的力平衡方程:

(23)

为了简化计算，可以忽略保持架与滚子之间的摩擦力，可得滚子的力矩平衡方程为

(24)

将求解载荷分布得到的最大接触力代入式(11)、(12)、(13)和(14)。最后结合公式(19)—(24)整理得到式(25)和式(26)。

(25)

(26)

2 考虑粗糙度和微极流体的弹流润滑模型

2.1 滚子几何模型

由于滚子和滚道表面不是绝对光滑的，同时粗糙度与油膜厚度处在同一数量级上，因此在弹流润滑计算时应考虑表面粗糙度的影响。粗糙表面的滚子与粗糙表面的滚道之间的润滑可等效成一个滚子与粗糙平面之间的润滑，如图3所示为滚子的几何模型平面图。Rx为滚动方向上的最大曲率半径，Rc是滚子边倒圆中心到y轴的距离，yc是滚子边倒圆的中心到x轴的距离，Ry为滚子凸度半径，lc为滚子边倒圆的长度，r为滚子边倒圆半径，δ为滚子凸度。

因此，滚子与平面之间的初始间隙为

(27)

2.2 弹流润滑模型

研究有限长滚子的弹流润滑问题，这里需要考虑到滚子与滚道接触面水平方向上x和y2个方向。假设不考虑y方向上的速度，且x方向上的速度不发生变化。由此可得二维稳态弹流润滑的雷诺方程[19-20]为

(28)

式中：ρ为润滑油的密度(kg/m3)；η为润滑油黏度(Pa·s)；p为油膜压力(Pa)；us为卷吸速度(m/s)；h为润滑油的膜厚(m)；N是量纲一参数，称为耦合数，因为它描述了线性动量方程和角动量方程的耦合，当N等于0时，线性动量方程与角动量方程解耦，线性动量方程退化为经典的Navier-Stokes方程；lf为特征长度，因为它描述了微极流体和油膜间隙之间的相互作用，它等价于修正雷诺数方程的黏性项。

(29)

膜厚方程表达式[21]如下：

(30)

黏度与密度是与压力p相关的函数，其计算公式如下：

(31)

(32)

式中：η0为润滑油初始黏度；ρ0为润滑油初始密度。

中心油膜厚度由载荷平衡方程控制，方程为

(33)

3 数值方法

在对滚子润滑可靠性的研究中，应考虑滚子承载最严重的区域。因此，接下来的研究重点是在最大受载下滚子的润滑问题。在轴承运行过程中，轴承的载荷必然会影响轴承的转速。因此，通过轴承动力学计算，可以求出载荷和相应的转速。

1.2.4 裸鼠移植瘤模型构建取对照组、阴性组、干扰组CaSki细胞，用0.25%胰蛋白酶消化液将细胞消化，1000 g离心10 min，把上清溶液吸弃，添加PBS，将细胞配制成每毫升含有4×107细胞的单细胞悬浮液，吸取300 μL注射至裸鼠右侧后腿皮下，裸鼠均出现移植瘤。分别在接种CaSki细胞后7、12、17、22、27 d测量肿瘤体积，肿瘤体积=（长径×短径2）÷2。在最后1次测量肿瘤体积后，脱臼法将裸鼠处死，取肿瘤组织，称取肿瘤质量。

根据图4左边的框图求解载荷分布的非线性方程的自变量为轴承间隙δc和内圈接触载荷Qij。首先将轴承间隙δc和接触载荷Qij的初值代入式(7)—(10)中，然后用牛顿法迭代求解。通过调整轴承间隙δc大小，当式(6)左右两侧差小于10-10时，判定为收敛。通过与仿真软件进行结果对比，检验计算结果的合理性。式(25)和式(26)的变量为保持架的转速ωc和滚子的转速ωj。采用Levenberg-Marquardt方法求解该非线性方程，直到最小误差小于10-10。

图5所示为求解有限长圆柱滚子轴承弹流润滑的流程。将通过求解轴承动力学得到的轴承最大载荷和滚子转速代入弹流润滑方程，利用中心和向前差分格式离散量纲一化雷诺方程、膜厚方程和载荷方程，得到各节点压力、中心膜厚度和油膜厚度的非线性代数方程，然后用牛顿法得到压力分布和膜厚分布。

从上述求解得到的压力分布和油膜厚度分布中，可以得到轴承运行中最危险的点，即最小油膜厚度处。然后，通过合理的实验设计获得需要被拟合的数据，采用差分进化算法拟合得到最小膜厚显式方程。最后采用一阶二阶矩中心点法进行可靠性分析。可靠性分析的极限状态方程如式(34)[22-23]所示。

g(X)=Hmin-3σ

(34)

式中：Hmin为拟合得到的最小膜厚；σ表示等效粗糙度均方根偏差。

一次二阶矩可靠度计算公式[24]为

(35)

式中：μXi为输入参数的期望值；σXi为输入参数的方差。

4 算例与结果分析

选取SKF公司的N210EC轴承，轴承参数及工况见表1。

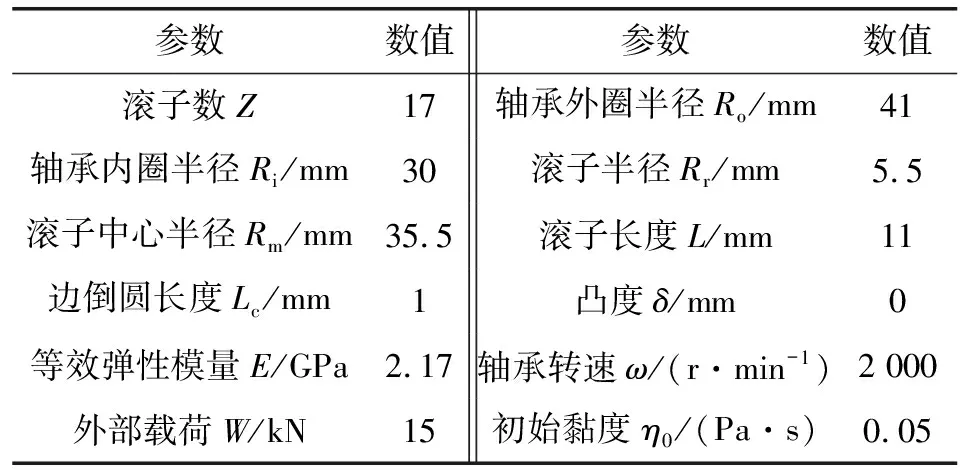
表1 轴承参数及工况

4.1 轴承动力学

根据表1中的参数，通过求解式(6)—(10)可得到轴承各滚子的加载情况。

轴承各个滚子上的受载情况分布如图6所示。

根据计算结果，滚子的最大载荷为6 056.9 N。

先在Romax DESIGNER软件中创建箱体，添加轴部件，随后依据轴承参数创建圆柱滚子轴承，将轴承安装于轴上，然后添加15 kN的点载荷，在轴的两端添加功率载荷。建立的圆柱滚子轴承动力学模型如图7所示。

静力学分析后可得载荷分布雷达图，如图8所示。可以看出，滚道最大载荷为5 969.2 N，计算值与仿真值之间的误差仅为1.45%。

将滚子所受的最大载荷和表1中的参数代入轴承动力学方程求解，可得滚子的自转速度为6 286 r/min，滚子的公转速度为837 r/min。

4.2 有限长滚子弹流润滑

图9显示了微极流体参数对润滑油膜厚度分布的影响。X为滚子径向的接触宽度，与滚子长度不在一个数量级上，且要小得多，因此这里就选择量纲一化形式来表示，Y为滚子长度。从图中可以看出，微极性流体的油膜厚度大于普通流体，但“边缘效应”无法消除。图10显示了微极流体参数对膜压分布的影响。图10(a)所示为普通流体的压力分布，图10(b)所示为微极流体下的压力分布，对比两图可得出，求解域中的微极流体的油膜压力略低于普通流体，“边缘效应”仍然存在。

粗糙表面具有许多表面特征，常用的粗糙度模型由高度分布参数和自相关函数描述。WHITEHOUSE和ARCHARD在1970年实验中发现粗糙度服从高斯分布，因此，文中采用粗糙表面数字仿真来生成服从高斯分布的轴承表面粗糙度，从而使得润滑计算的结果更能反映真实的润滑状态。如图11所示，横截面粗糙度沿各坐标轴为高斯分布，最大粗糙度幅值为0.5 μm，两表面粗糙度的算术平均值为0.312 5 μm。

根据图11所示的粗糙度分布，计算了圆柱滚子的弹流润滑结果，并与光滑解进行了比较。

图12显示了凸度变化对油膜厚度和压力分布的影响。当δ=0时，最小膜厚出现在滚子两侧的端部。随着凸度的增加，滚子端部的润滑状况逐渐改善，油膜分布将沿滚子轴向向中部集中。结果表明，滚子凸度的增加使得滚子端部的膜厚增加，压力减小，避免出现边缘应力集中,且形成了完整的润滑油膜可更好地平衡外载荷，保护接触副表面，可以改善滚动轴承的“边缘效应”，避免润滑失效。

由图12(b)和图12(d)可知，沿X轴正方向，压力值先增大后减小，最大值靠近出油口处。当δ=0时，滚子两侧会有较高的油膜压力。但随着凸度的增大，“边缘效应”逐渐改善，压力分布沿滚子轴向向中间集中，辊中间出现较高压力。

从图12(c)、(d)中可以清楚地看到，粗糙表面的油膜厚度小于1.0 μm的区域明显大于光滑表面的区域；同时，粗糙表面的油膜压力大于3.0 MPa的区域也略大于光滑表面的区域并且压力分布会有所波动。这是由于粗糙峰使得两接触面的初始间隙变小，并且在一定的流量条件下，流速增大，导致油膜压力增大。同时相较于光滑表面，滚动轴承所承受的载荷由润滑油膜所承担转变为由润滑油膜和表面粗糙峰共同承担，为了使得油膜厚度形状平滑，油膜压力将在粗糙峰处增大，将粗糙峰“压平”。因此，在轴承润滑过程中，滚子与滚道接触区域的润滑状况比理想状态下的润滑状况差很多。

4.3 改进的最小膜厚方程

为了评价轴承的润滑性能，必须进行可靠性分析，可靠性分析需要显式的最小油膜厚度表达式。因此，为拟合最小膜厚方程而选择的输入参数范围如表2所示。根据轴承的实际工作情况，选择载荷、转速和材料参数的范围。粗糙度的选定范围为0.1～0.45 μm。量纲一微极流体参数的选择范围为0.1～0.7。

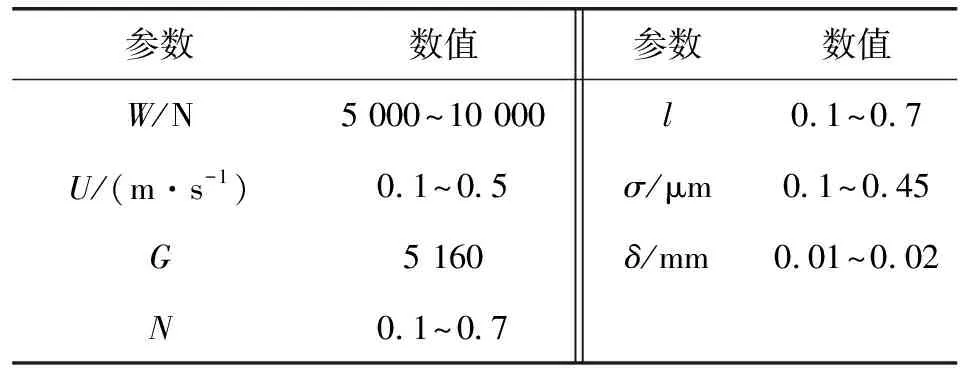
表2 参数范围

对于膜厚，在不考虑表面粗糙度的情况下，假设方程的形式为c1Wc2Uc3Gc4，这种形式被许多文献所采用，可以通过简单的计算获取最小膜厚的信息。文中在上述形式基础之上，乘上一个考虑表面粗糙度和微极性流体的影响因子，得到最小膜厚的形式为

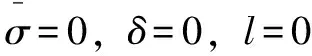
表3 最小膜厚方程拟合数据

改进后的薄膜厚度方程为

Hmin=2.013W-1.030U0.686G-0.5379×(1-

(36)

在实际工作条件下，采用简单随机抽样选取的12组数据检验膜厚方程的准确性，结果如表4所示。最大误差为7.14%，最小误差为0.65%，平均误差是3.43%。由于公式拟合过程中，参数过多，参数的取值与范围都会对拟合公式的准确性产生一定影响，这是不可避免的。因此确保拟合公式最大误差在可接受范围内即可。显然，除采样点外，最小膜厚的拟合方程仍然能够保证一定准确性。

表4 改进后的最小膜厚公式拟合数据

表5给出了改进的膜厚方程与未考虑表面粗糙度和微极流体的弹流润滑数值分析结果的比较。研究的工况为：W=5 000 N,U=0.2 m/s,G=5 160,σ=0.312 5 μm,l=0.5,N=0.5,δ=0.01 mm。

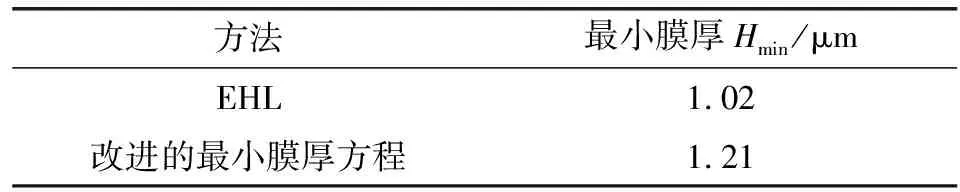
表5 方法计算对比

在相同工况下，弹流润滑计算结果为1.02 μm，改进的油膜厚度方程计算结果为1.21 μm，误差为15.70%。微极流体中固体颗粒的作用等同于增加了润滑油的等量黏度，因此使得整体的润滑油膜增大，最小膜厚也会相应增加。当粗糙度存在时，两接触表面若出现波谷与波谷相对时，该区域的润滑油膜则会有一定程度的增加。当两者的影响叠加时，最小膜厚会趋于增大。结果与NADUVINAMANI和KASHINATH[25]的结果一致。因此，该拟合方程可以很好地替代考虑表面粗糙度和微极流体的圆柱滚子轴承弹流润滑计算，并可代替复杂的弹流润滑计算进行可靠性分析，大大简化了计算过程。

图13显示了在上述工况下，载荷和转速的标准差变化对轴承润滑可靠性的影响。当载荷和速度的标准差较小时，标准差的波动对润滑可靠性影响不大。随着载荷和速度标准差的不断增大，润滑可靠度也呈线性下降。因此，保证轴承工作状态的稳定性是保证可靠润滑的首要目标。