转/静子齿对迷宫密封泄漏特性与动力特性影响机制研究*

2022-05-19孟继纲王小伟

润滑与密封 2022年3期

白禄孙丹赵欢孟继纲王小伟周敏

(1.沈阳航空航天大学航空发动机学院辽宁沈阳 110136；2.沈阳鼓风机集团股份有限公司,辽宁重大装备制造协同创新中心辽宁沈阳 110142)

迷宫密封是航空发动机、燃气轮机、压气机等透平机械的关键部件，对于节能降耗与防止工作介质的泄漏起着关键作用[1]。此外，密封间隙内存在泄漏流体，泄漏流体在转子运转的过程中会产生流体激振力，从而导致转子系统的不稳定振动[2-4]。迷宫密封的进气条件、介质参数、密封齿的形状与设计位置等因素均对迷宫密封的性能产生影响，其中，密封齿的设计位置对迷宫密封性能的影响较大[5-8]，研究密封齿设计位置对迷宫密封泄漏特性与动力特性的影响具有重要理论意义和工程应用价值。

自20世纪80年代以来，学者们对迷宫密封开展了大量研究。1986年CHILDS和SCHARRER[6]通过实验分别对转子齿与静子齿迷宫密封进行了研究，并分析2种结构的动力特性。PICARDO和CHILDS[7]研究了静子齿迷宫密封的转子动力学系数，比较测量值和理论值，并与孔型静子密封进行比较。HAWKINS等[8]对带有蜂窝状静子的迷宫式气体密封进行实验研究，将与光滑的静子密封件进行比较，并通过理论进行预测。MEHTA[9]对不同齿形的迷宫密封进行研究，并比较了直齿与斜齿2种齿形迷宫密封的泄漏量与动力特性系数。ARTHUR和 CHILDS[10]测得了转子齿迷宫密封的转子动力学系数和泄漏量，并与静子齿迷宫密封进行了比较。陈尧兴等[11]研究了进口预旋对迷宫密封动力特性影响。孙丹等人[12]对气体介质参数进行了研究，并得出其对迷宫密封静力与动力特性的影响机制。陈慈伟和张万福[13]研究了转子倾斜对迷宫密封动静特性的影响。李伟等人[14]对涡轮叶尖迷宫式密封进行研究，并用数值模拟的方法，研究了该密封结构对泄漏流场的影响。贾兴运等[15]在转子振动的情况下，对T型交错式迷宫密封进行研究，得出转子振动对密封性能的影响。王炜哲等[16]通过实验测量和数值模拟2种方法对迷宫密封的动力特性进行研究。陈尧兴等[17]在迷宫密封齿蘑菇形磨损时，对迷宫密封进行了泄漏特性与动力特性的研究。上述文献在研究密封时大多通过改变迷宫密封齿的结构、密封介质的参数、进出口的边界条件等来研究迷宫密封的泄漏特性与动力特性，对于迷宫密封齿在转子上与静子上对密封性能的影响的研究较少，鲜有关于迷宫密封齿的设计位置对迷宫密封泄漏特性与动力特性影响机制研究的报道。

本文作者建立了迷宫密封泄漏特性与动力特性多频椭圆涡动求解模型，分析了转/静子齿迷宫密封的泄漏特性与动力特性，揭示了转/静子齿迷宫密封泄漏特性与动力特性影响机制，并总结出2种结构对迷宫密封转子系统稳定性的影响。文中研究成果为迷宫密封齿的优化设计提供理论依据。

1 迷宫密封泄漏特性与动力特性理论模型

1.1 迷宫密封泄漏特性理论模型

图1(a)所示为静子齿迷宫密封气流流动示意图，图1(b)所示为转子齿迷宫密封气流流动示意图。图中p1为高压侧，p2为低压侧，气流从p1侧流入，从p2侧流出。

1908年，MARTIN[18]用热力学原理分析了理想迷宫密封模型的流动特性，该模型将各密封齿视为一连串喷嘴，并假设密封在亚临界工况下工作，流动为等温过程，流速在声速范围内，且不考虑透气效应。MARTIN在该种工况下提出的泄漏量计算公式为

(1)

气体常数计算公式为

Rg=R/M

(2)

式中：A=πDδ，为迷宫密封的泄漏面积；Cd为流量系数；z为迷宫密封齿数；p2为密封出口压力；p1为密封进口压力；T为密封进口温度；R为理想气体常数；D为转子直径；δ为密封间隙。

该公式的局限性与计算误差均相对较大。EGLI[19]通过实验对直齿型迷宫密封的泄漏量进行研究，并对MARTIN公式进行了修正：

(3)

当气体为理想气体时，k=γ，其中，k为比热容比。

文中用EGLI公式对迷宫密封的泄漏量进行求解。定义如下物理量：

(4)

(5)

式中：i=1，2；qm1与qm2分别为不考虑泄漏系数时静子齿与转子齿迷宫密封的泄漏量，为文中理论计算所用物理量；Qm1与Qm2分别为考虑泄漏系数时静子齿与转子齿迷宫密封的泄漏量，为文中数值模拟所用物理量。

1.2 迷宫密封动力特性理论模型

根据转子小位移涡动理论[20]，转子受到微小位移和速度扰动时，可将转子受到的气流力与扰动位移和扰动速度的关系线性化表示为

(6)

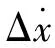
转子涡动方程为

(7)

(8)

考虑转子对密封动力特性系数影响后，式(6)可写为

(9)

对式(9)进行快速傅里叶变换，可得到频域内密封气流力变化量与密封动力特性系数和微小扰动位移的关系式为

(10)

将转子多频涡动位移方程式(7)与式(8)分别代入到式(10)中，整理可得：

(11)

(12)

定义阻抗系数Huv为

(13)

将阻抗系数式(13)代入到式(11)与式(12)，整理化简后，得到阻抗系数为

(14)

通过阻抗系数可得到密封动力特性系数，如式(15)所示。

(15)

2 迷宫密封泄漏特性与动力特性数值求解模型

2.1 求解模型

文中所研究的2种密封结构如图2所示，其中图2(a)所示为静子齿迷宫密封结构，其迷宫密封齿设计于静子表面，转子表面光滑，图2(b)所示为转子齿迷宫密封结构，其迷宫密封齿设计于转子表面，静子表面光滑。图3(a)、(b)分别为静子齿与转子齿迷宫密封的几何参数。

为比较二者的泄漏特性与动力特性，转子齿迷宫密封采用与静子齿迷宫密封相同的齿形结构和工况参数，如表1所示。

表1 工况参数

2.2 网格划分及无关性验证

图4所示是迷宫密封数值求解模型轴向网格划分截面，通过改变网格的数量，分析其对迷宫密封泄漏量的影响。为选取合适的网格数量，静子齿迷宫密封改变其节点数时，泄漏量变化如表2所示；转子齿迷宫密封改变其节点数时，泄漏量变化如表3所示。由表2可知，静子齿迷宫密封划分方法2所得到的泄漏量比划分方法1多0.4%，划分方法3所得到的泄漏量比划分方法2多0.1%；由表3可知，转子齿迷宫密封划分方法2所得到的泄漏量比划分方法1多0.29%，划分方法3所得到的泄漏量比划分方法2多0.12%，此时增加节点数对结果影响不大，因此最终选取划分方法1，所得网格数为210万。

表2 网格密度对静子齿迷宫密封泄漏量的影响

表3 网格密度对转子齿迷宫密封泄漏量的影响

2.3 边界条件与数值方法

迷宫密封数值求解模型的边界条件如下：入口、出口设定为压力边界条件，入口设为总压，出口设为静压，气流流动皆沿轴向且垂直于入口、出口边界。静子齿与转子齿迷宫密封的静子面设定为无滑移边界条件，转子面设为旋转边界条件，转速为11 096 r/min，同时做多频椭圆涡动。

将转子齿与静子齿2种密封结构的多频涡动振幅a和b分别设置为a=2.92×10-3mm、b=1.46×10-3mm，转子涡动频率为40～320 Hz，共8个频率成分。根据采样定理，考虑到计算精度和计算时间等因素，将采样频率确定为10 kHz，即非定常计算的时间步长为1×10-4s，当相邻两周期转子涡动到同一位置处，密封气流力的波动小于0.2%，可认为非定常计算收敛。

2.4 数值求解模型准确性验证

为验证迷宫密封数值求解模型的准确性，将数值求解模型计算结果与理论计算结果和文献[21]中Tascflow计算得到的泄漏量进行比较。由表4可知，Tascflow计算结果与文中数值求解模型的相对偏差为0.28%，由公式(5)计算出的理论值与文中数值求解模型的相对偏差为0.46%，从而验证了文中数值求解模型的准确性。

表4 数值模拟、理论计算与文献[21]泄漏量的比较

3 转/静子齿对迷宫密封泄漏特性与动力特性的影响及机制分析

3.1 转/静子齿对迷宫密封泄漏特性的影响及机制分析

3.1.1 转/静子齿对迷宫密封泄漏特性的影响

图5所示为迷宫密封进出口压比与泄漏量的关系。可以看出，随着压比的增大，转子齿与静子齿迷宫密封的泄漏量均增加。这是因为当进出口压比增加时，密封间隙内射流增大，密封腔体内压力回升，动能转换成热能不足，从而使得密封性能下降。

图6显示了转速与泄漏量的关系。可以看出，在高转速下，转子齿与静子齿迷宫密封的泄漏量均随转速的增加而减小。这是因为随着转速的增加，转子与静子之间的有效通流面积减小，因此通过齿顶间隙的泄漏量减小。

3.1.2 转/静子齿对迷宫密封泄漏特性影响机制分析

迷宫密封的泄漏区域由射流区与腔内流区2部分组成(如图7所示)，其中射流区部分占主体。由公式(4)与(5)可得出影响转/静子齿迷宫密封泄漏量的因素为流量系数Cdi与泄漏面积Ai。比较2种模型在不同压比下的流量系数与泄漏量，结果如图8所示。转/静子齿迷宫密封的理论计算公式与数值模拟公式之间只差了流量系数Cdi。从图8中可以看出，随着压比的增加，转/静子齿迷宫密封的流量系数变化不大，且2种结构流量系数的相对偏差为0.87%，因此引起转/静子齿迷宫密封泄漏量存在差别的原因并非流量系数的不同，而是2种密封结构的泄漏面积不同。

图9(a)为静子齿迷宫密封泄漏面积示意图，图9(b)为转子齿迷宫密封泄漏面积示意图。引起流体泄漏的主要区域为腔内流区，该泄漏区域的轴向截面可看成环形，环形的内径为转子的直径、外径为迷宫密封件的直径。如图9所示，静子齿迷宫密封的泄漏面积S1=πD1δ1，转子齿迷宫密封的泄漏面积S2=πD2δ2。其中，D1为静子齿迷宫密封的环形泄漏面积内径，D2为转子齿迷宫密封的环形泄漏面积内径。通过图9中给出的几何参数得出：转子齿迷宫密封的泄漏面积S2比静子齿迷宫密封的泄漏面积S1大2.38%，且从图8中可以看出，转子齿迷宫密封的泄漏量始终比静子齿迷宫密封大2.58%～3.49%，故转/静子齿迷宫密封泄漏量的差别归因于二者的泄漏面积不同。

3.2 转/静子齿对迷宫密封动力特性的影响

3.2.1 转/静子齿对迷宫密封动力特性系数的影响

图10给出了转子齿与静子齿迷宫密封在40～320 Hz转子涡动频率下的动力特性系数。由10(a)可知，在低频下，转子齿与静子齿迷宫密封的交叉刚度均为负值，且转子齿迷宫密封交叉刚度的绝对值大于静子齿迷宫密封；而在高频下，随着转子涡动频率的增加，转子齿迷宫密封的交叉刚度由负变正，静子齿迷宫密封的交叉刚度仍为负值，但其绝对值减小。根据激振力与转子动力特性系数的关系[22]可知，当交叉刚度Kxy的值为负时，泄漏流体所产生激振力的方向与转子的涡动方向相反，从而抑制了转子系统的失稳。因此，在低频时，转子齿与静子齿迷宫密封均对转子系统的稳定性有利；而在高频时，转子齿迷宫密封的交叉刚度由负变正，当交叉刚度Kxy为正时，泄漏流体所产生激振力的方向与转子涡动方向相同，促进了转子系统的失稳，而静子齿迷宫密封的交叉刚度仍为负，虽然抑制转子系统失稳的能力降低，但在使转子系统稳定性方面远好于转子齿迷宫密封。

由10(d)可知，随着转子涡动频率的增加，静子齿迷宫密封的直接阻尼逐渐减小，但其值大于转子齿迷宫密封。根据激振力与转子动力特性系数的关系[22]可知，正直接阻尼将产生一个与转子涡动方向相反的切向激振力，同样起到抑制转子失稳的作用。随着转子涡动频率的增大，流体的流动状态越发混乱，阻尼效果减弱，由图中可以看出，静子齿迷宫密封的直接阻尼始终大于转子齿迷宫密封，因此静子齿迷宫密封更有利于转子系统的稳定。

而直接刚度系数Kxx、Kyy反映的是密封腔室内气流对转子固有频率的影响，当密封直接刚度为正值时，转子的固有频率和临界转速均随之增大。由10(b)可以看出，静子齿迷宫密封的直接刚度系数为正，转子齿迷宫密封的直接刚度系数为负，静子齿迷宫密封使得转子有更高的固有频率，因此静子齿迷宫密封更有利于转子系统的稳定。

为综合反映密封动力特性对转子系统稳定性的影响，定义有效阻尼Ceff与有效刚度Keff如下：

Ceff=Cxx-Kxy/Ω

(16)

Keff=Kxx+CxyΩ

(17)

从图11中可以看出，静子齿迷宫密封的有效阻尼比转子齿迷宫密封的有效阻尼大。有效阻尼的值越大越有利于转子系统的稳定，因此静子齿迷宫密封相比转子齿迷宫密封而言更利于转子系统的稳定。从图12中可以看出，静子齿迷宫密封的有效刚度为正，而转子齿迷宫密封的有效刚度为负，因而进一步确定了静子齿迷宫密封更有利于转子系统的稳定。

3.2.2 转/静子齿对迷宫密封动力特性影响机制分析

图13所示为预旋比为0时转/静子齿迷宫密封所受气流激振力与速度矢量图，图14所示为预旋比为0.2时转/静子齿迷宫密封所受气流激振力与速度矢量图。其中x表示径向，y表示切向，Fr为径向气流力，Ft为切向气流力，F为转子所受气流激振力的合力。从图13中可以看出当预旋比为0时，转子齿与静子齿迷宫密封中的转子均在做逆时针涡动，2种结构的转子所受切向气流力的方向向下，切向速度的方向向上，二者的方向相反，切向气流力抑制了转子自身的涡动。对比图13中的两幅图可以看出，转子齿迷宫密封的切向气流力小于静子齿迷宫密封，二者虽然都对转子的涡动起到了抑制作用，但静子齿迷宫密封对转子涡动的抑制能力比转子齿迷宫密封的抑制能力强。从图14中可以看出，加入预旋比后，2种结构的转子所受切向气流力的方向向下，切向速度方向向上，二者的方向仍相反，切向气流力仍抑制转子自身的涡动。且从图14中的两幅图可以看出，静子齿迷宫密封的切向气流力比转子齿迷宫密封大，仍能得出静子齿迷宫密封对转子涡动的抑制能力比转子齿迷宫密封的抑制能力要强。因此可以得出，静子齿迷宫密封更有利于转子系统的稳定。