培养初中学生数学讲题能力的几点做法
2022-05-09邓健伟
邓健伟
在数学课堂培养初中学生的数学讲题能力,其所立足的便是“学生为本,学为核心”的基本教学原则,突出学生为主体,教师为主导,有效提高课堂教学质量。每节课的前半节,让学生依托于小组合作学习,展开数学学习。之后则为小组学习成果、知识盲点的展示阶段。教师则充分发挥自身的引导作用,适时归纳、点拨,使教学活动能够得以进一步发展。在此种数学教学活动的过程中,讲题教学便会被成功地融入到其中。
关键词:初中数学 讲题能力 培养做法
一、初中学生数学讲题教学的重要性
初中数学教学开展的过程中,至少有一半的课堂教学是围绕着习题、例题教学展开的。同“掌握数学就是善于解题”所阐述的道理相近,数学教育同讲题之间属于一种相辅相成的关系。如果教师在进行课程教学的过程中,采取的是传统的一讲到底的教学方式,学生会处在相对被动的位置,这就使得学生在学习的过程中,出现枯燥乏味的情况,甚至在一些时候,有些学生还会为此出现打瞌睡的问题,教学的效果必然不会明显。在数学课堂中注意讲题能力的培养,学生的主体作用往往能够得到充分地发挥。因为此种教学模式,在教学活动开展的初期,能充分发挥学生的主观能动性,所以使得学生能够大胆且主动地去尝试讲题[1]。
二、初中学生数学讲题能力的培养方法
(1)合理建立学习小组,为学生讲题提供团队保障。合理组建学习小组,能为学生讲题提供团队保障,有利于开展学生的讲题活动。如,笔者在接手本班学生后,根据异质分组、组间同质原则,学习借鉴“导学案+小组合作”课堂模式的方法,也对本班学生进行了小组合作学习的建设。本班共有学生54人,分为9组,每组6人,根据成绩平均分组,每组1号成绩最好,6号最差,各组平均成绩基本相同,如遇到小组成员全部或1人为男生或女生,则进行微调,原则上是同号调节,1、2号为正副组长,分组原则是:性别比例、学业成绩、性格特点、兴趣倾向、交往能力、品行状况。通过组建学习小组,充分发挥学习小组的作用,兵教兵,兵练兵,独学、对学、群学相组合,学生请教学生,方便快捷,有共同语言,没有距离感,更便于交流,极大地保障了自学效果,5、6号由不会到会,自信心逐步得到提高,组与组之间展开竞争,小组文化搞得红红火火,班内学习氛围更加浓厚了。
在具体组建学习小组的过程中,教师可以让学生自愿结组,同时也可以依据“组间同质,组内异质”的原则,对学习小组进行划分,分为组长、副组长、记录员、汇报员等,每一位成员都有具体的分工,大家都是参与者而不是旁观者,保证每个学习小组都有各个学习层次的学生,并明确学习小组的制度,继而为讲题活动的展开奠定基础[2]。
(2)鼓励学生积极参与,为学生创设讲题机会。在建立数学学习小组后,教师应鼓励学生积极讨论问题,并对学生进行科学地引导,使学生能够从念出答案发展到能够讲出解题的思路,以此来落实对学生解题能力的培养。如在学习“一元一次方程”的过程中,笔者便通过设置问题的方式,让学生对教学内容进行讨论。在这过程中,笔者给学生设置了方程2x+a=1与方程3x-1=2x+2的解相同,a的值为多少的问题,之后让学生围绕这个问题进行讨论学习,而在讨论结束之后,笔者便让学生将具体的解题思路讲出来,并鼓励有不同想法的同学说出自己的思路,各抒己见。后面有的学生认为,应先将第二个方程中的x解出来,之后在将x的值代入到第一个方程中,从而最后得出a的值为-5。
板书:3x-1=2x+2 把x=3代入 2x+a=1得
3x-2x=2+1 2x3+a=1
x=3 a=-5
再如學习“全等三角形”的过程中,一共有:SSS、ASA、SAS、AAS四种方法去求证,如果求证直角三角形全等还可以用HL。对于具体的题目要具体去分析,有的学生喜欢常用其中一种判定去求证,证不出来再去想其他判定,在小组内讲题出现很多分歧,效率不高。笔者引导他们从已知条件出发,看已知条件和隐藏条件满足哪一种判定,然后再整理思路在小组内分享,这样在组内讲题就顺畅多了。有的学生在选取判定方法时用了兜圈方式,把求证过程复杂化,这就要教师慢慢去引导,即使有时走了弯路,也是值得的,因为学生在讲的时候暴露了思维过程,利于教师适时点拨帮助其优化解题方法。
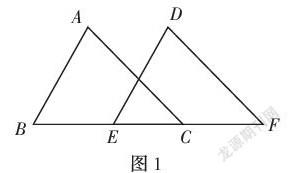
例如:如图1,已知:点B、E、C、F在同一直线上,AB=DE,AB∥DE,AC∥DF,BE=CF。
求证:△ABC≌△DEF
鼓励学生大胆地将自己的想法说出来,即使说错也没有关系,只要是讲出自己的解题思路都应该被鼓励。为学生创设讲题机会,鼓励学生积极投入到教学活动中,有助于促进学生对知识的把握。
(3)做好学生讲题点评,反馈学生讲题效果 。教师在学生讨论、讲题阶段落实之后,应对学生的讲题思路以及技巧等,进行点评考量。这期间,教师应对学生在解题过程中呈现出的优点,进行放大。
如学习“四边形”的过程中,求证一个四边形是平行四边形、菱形、矩形还是正方形?有学生讲题时分析是按顺序一步一步的思路去解题,有的则用逆向思维的方式去跟同学们讲题,这种几何证明题的分析法是很应该被鼓励的和运用的,由结论倒回来证明,所需要的条件都可以在已知和隐藏的条件去找,这样的讲题方式会打开同学们的不同思路,让他们耳目一新,听起来津津有味。
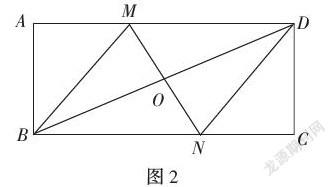
例如:如图2,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN。
(1)求证:四边形BMDN是菱形(2)若AB=4,AD=8,求MD的长
学生说:要证明一个四边形是菱形,最快的方法就是求证它的对角线互相垂直平分,即BD⊥MN和BO=DO、MO=NO,题目已知给出BD⊥MN和BO=DO,我们只要求出MO=NO即可,要求MO=NO,只需求证△BON≌△DOM,用ASA(角边角)就可以证明△BON≌△DOM。学生讲完后同学们自觉响起了掌声,笔者也在班上给予表扬,表扬其逆向思维的证明方法,要求同学们向其学习,极大地增强其继续努力学习的信心。
总而言之,在初中数学的教学过程中,对学生的讲题能力进行培养,有着极其现实的教育意义。因此,在初中教学活动开展的过程中,初中数学教师应依托于教学实践,积极开展数学讲题教学,帮助学生提升数学解题能力,使学生能够在数学学习中得到发展,从而为其日后更好的学习数学奠定基础,继而推动我国教育事业的长远发展。
参考文献:
(1)王朝晖,利用学生“讲题”,提高初中生数学抽象能力[J].数学学习与研究,2019(17):44.
(2)王德贵,王朝晖。初中数学课堂学生“讲题”能力的培育[J].福建基础教育研究,,2019(10):66-68.
