柔顺停歇机构伪刚体模型的运动学和动力学分析

独亚平，赵春花，郭嘉辉，周 川，张立强

（上海工程技术大学机械与汽车工程学院，上海 201620）

柔顺机构是一种利用自身柔性构件的变形来转换运动、力和能量的新型机构［1-2］。与传统刚性机构相比，它免去了运动副间的装配、摩擦和磨损，在很多特殊场合得到应用，近年来成为机构学领域的一个研究热点。虽然柔顺机构具有独特的性能和广泛的应用，但由于柔性构件在运动过程中会产生大变形行为，这种几何非线性行为增大了柔顺机构分析和设计的困难［3-4］，阻碍了其更深入的发展。为了较简便地分析柔顺机构，Ling等［5］提出了伪刚体模型法，用具有等效的力与变形关系的刚体构件来模拟柔性构件的变形，目的是将柔顺机构的非线性问题转化为等效刚性机构的线性问题来求解，这为柔顺机构的进一步研究奠定了基础。由于最初提出的1R伪刚体模型对大变形柔顺杆的模拟精度不高［6］，研究者通过增加模型中转动副的个数或考虑轴向变形的影响陆续提出了2R、3R、PR以及PRR等伪刚体模型以提高模拟精度［7-10］。

为了满足高效生产和多种工艺规范的要求，在许多机械自动生产线中，经常须将主动件的等速连续转动转变为从动件周期性的间歇运动，来进行加工、换位、分度、进给、换向、供料、计数和检测等工艺操作。含有该类从动件的机构称为停歇机构［11］，其主要应用在纺织、食品、印刷等轻工业的机械中。由于该类机构须长时间作周期性运动，其中的刚性杆件会因为相互摩擦而受到累积的损伤，最终导致机构发生疲劳失效。针对刚性停歇机构的缺点［12-13］，研究者在停歇机构中引入柔顺构件（如柔性杆、柔顺铰链等），以降低或者消除构件之间的摩擦、磨损，改善机构的运动性能［14］。此外，刚性机构实现间歇运动一般需要6～8根杆，而柔顺机构只需5根杆甚至更少，凸显了柔顺停歇机构的优势。Sonmez［15］在2000年和2007年分别设计了2种柔顺长停歇机构：一种由滑块、机械止动器、弹簧和扣梁组成；另一种由销接扣梁、滑块、曲柄和柔性弧组成。他研究了这2种机构的动态模型，提出了实现所需停留时间的设计步骤。2010年肯尼索州立大学机械工程系的Tekes等［16］设计了一种旋转停歇机构，采用了一种柔性折叠臂梁，并在滑动质量块上附加了曲柄从动件，利用状态反馈线性化和 PID（proportion-integration-differentiation，比例-积分-微分）控制器，通过滑块的运动来控制曲柄角。2019年Tekes等［17］又设计了一种部分柔顺的新型平移停歇机构，基于弹性理论研究了依赖于机构几何形状和载荷的弹性构件的运动学行为，通过实验测量和ADAMS（automatic dynamic analysis of mechanical systems，机械系统动力学自动分析）仿真验证了动力学分析结果的正确性。

随着柔顺停歇机构的不断设计和改进，其逐渐替代刚性停歇机构而广泛应用于自动化机械设备，例如包装机的送料机构、印刷机的进纸机构和装配机器人等［18］，对其性能的要求也越来越高。相比于传统的平面刚性连杆停歇机构，柔顺停歇机构虽然有很多优点，但也存在一些力学问题。譬如：如果长时间承受交变应力或者工作温度升高，其柔性构件会出现蠕变或者应力松弛等现象［19］。此外，柔性构件的固有频率不仅是反映机构动力特性的一个重要指标，也是影响机构动态性能的重要因素［20］。目前对柔顺停歇机构力学特性方面的研究较少。准确地对柔顺停歇机构进行建模并深入分析，将对柔顺停歇机构的优化及应用起到重要的作用。

基于此，笔者采用伪刚体模型法对一柔顺停歇机构进行建模，并进行相应的运动学和动力学分析。首先，基于大挠度理论对大变形柔性梁进行屈曲分析，拟合得到其载荷与位移的关系式，并根据柔性梁的受力特性及结合边界条件得到其对应的非线性弹簧伪刚体模型；其次，通过建立的机构伪刚体模型，运用牛顿定律建立机构的运动学方程，求解滑块位移随时间及曲柄转角的变化曲线，以此分析机构的运动特性；最后，推导机构的动力学方程，求解机构的固有频率，揭示机构固有频率与构件结构几何参数及材料性能参数之间的关系。

1 柔性梁等效伪刚体模型

柔顺机构的运动过程往往伴随着柔性构件的非线性大变形，因此采用便于分析的伪刚体模型法对柔顺停歇机构的柔性梁建模，并基于大挠度理论进行屈曲分析，为接下来机构的运动学和动力学分析打下基础。

柔顺停歇机构如图1所示。机构由两端铰接的初始状态为直梁的柔性长梁、预加载的柔性短梁、刚性曲柄、滑轨系统和驱动电机组成。图中：XB为电机支架与滑块中心之间的水平距离；XC为电机支架与短梁支架之间的水平距离；H为滑块中心与短梁支架之间的垂直距离。该机构其余的相关参数如表1所示。该机构主要利用柔性梁的屈曲行为获得间歇运动，其工作原理如下：当曲柄开始旋转时，滑块由于短梁的预加载不会移动；当短梁的预加载达到初始直柔性长梁的临界屈曲载荷时，滑块会快速到达右极限位置；滑块在返回过程中，因为短梁的翘曲，也会产生短暂停顿。

表1 柔顺停歇机构相关参数Table 1 Relevant parameters of compliant dwell mechanism

柔顺停歇机构柔性长梁的受力如图2所示。

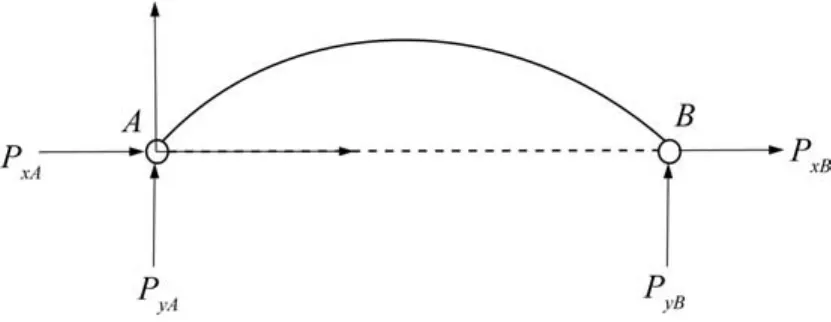
图2 柔性长梁的受力Fig.2 Stress of flexible long beam

分别求柔性长梁上水平和竖直方向上的力Px、Py，并对A点取矩，得到：

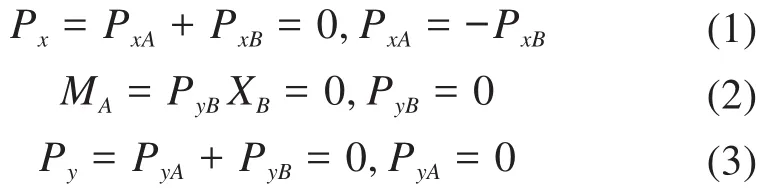
式中：PxA、PxB分别为柔性长梁左端和右端的水平分力；PyA、PyB分别为柔性长梁左端和右端的竖直分力。

通过以上静力分析可知，柔性长梁只受沿铰链相连方向的作用力，且其端点的变形也沿着与铰链相连的方向，如图3所示，这与弹簧的变形一致。

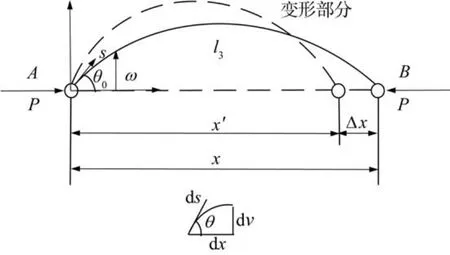
图3 柔性长梁的变形Fig.3 Deformation of flexible long beam

对于两端铰接、轴心受压的柔性长梁而言，其线性临界载荷Fcr3为：

式中：E为长梁的弹性模量，I3为长梁的惯性矩。

因为长梁在刚度最小的平面内弯曲，所以I3取横截面的最小惯性矩I3min：

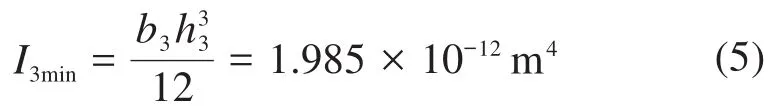
将相关参数值代入式（4），可以求得：

同理，可求得柔性短梁的临界线性载荷Fcr5为：

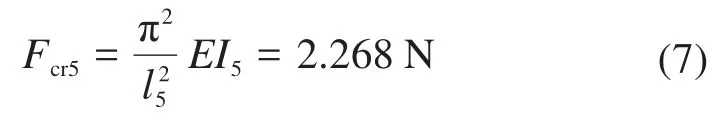
由于该柔顺停歇机构的柔性梁经历的是大变形，存在几何非线性，所以要根据大挠度理论求解其非线性临界载荷。由文献［21］可知大挠度柔性长梁基本微分方程是：

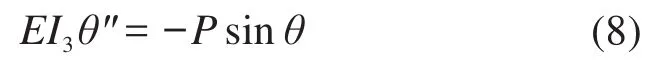
式中：θ为柔性长梁上任意一点处的转角；P为柔性长梁受到的轴向载荷。

对式（8）两边进行积分，得：

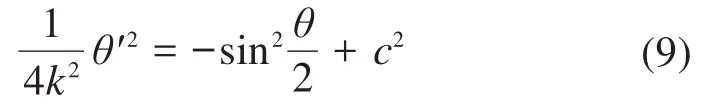
对式（9）取平方根，分离变量后得：

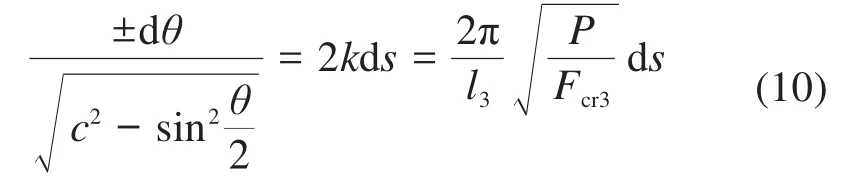
式中：ds为梁的长度微元；梁向上屈曲时取“-”，向下屈曲时取“+”。

如图3所示梁向上屈曲，则对式（10）取“-”，得：

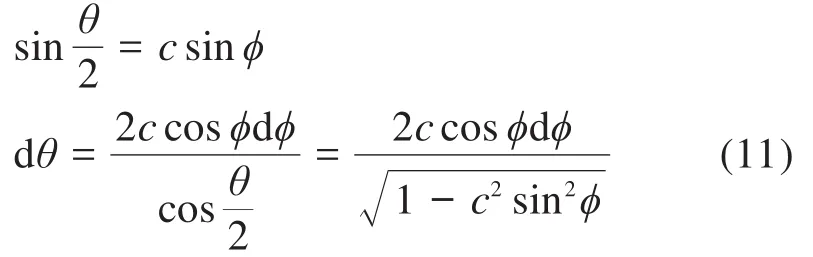
式中：φ为挠曲线转角，取值为（）。

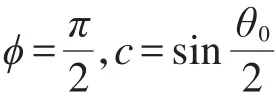
对公式（11）从梁的一端（s=0mm，）到梁的中点（，θ=φ=0°）进行积分，得：

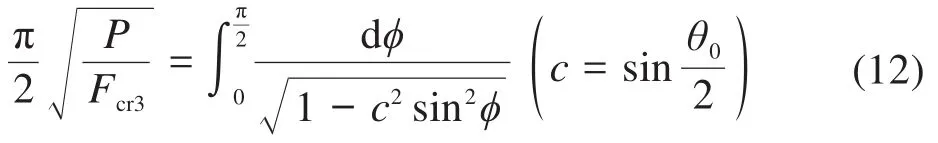
该积分称为第一类完全椭圆积分，表示横向载荷P与θ0之间的关系。

柔性长梁的初始轴向距离为x，现计算挠度v和变形后柔性长梁的轴向距离x′。针对梁的向上屈曲，根据式（10），可得：

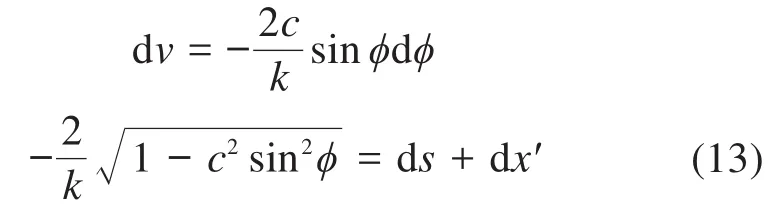
从φ=0°到进行积分，得到柔性梁上任一点关于s和θ的函数v和x′为：

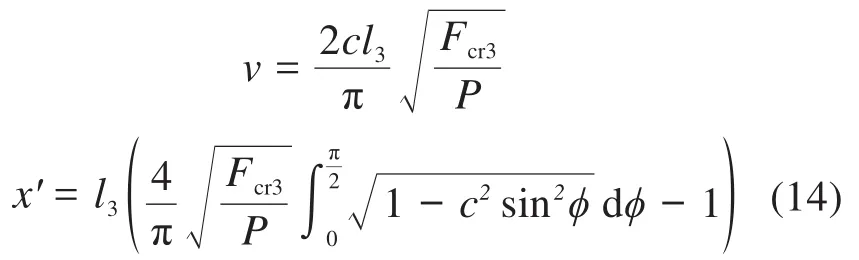
式（14）为第二类完全椭圆积分。

由图3可知，最大挠度位于柔性长梁的中点，因此该梁的最大挠度vmax和x′的精确解为：

由于本文中柔顺停歇机构柔性梁铰接两端不承受任何力矩，所以可基于弹性理论来求得载荷-位移曲线。根据以上对柔性梁的屈曲变形分析，并结合柔性构件的实际受力情况，则采用第一类和第二类椭圆积分的高度隐式控制微分方程［21］可以定义为：

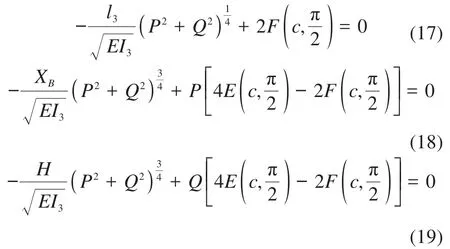
式中：Q为柔性长梁的垂直加载力；和是第一类和第二类完全椭圆积分，其详细定义可以参考文献［1］，为：

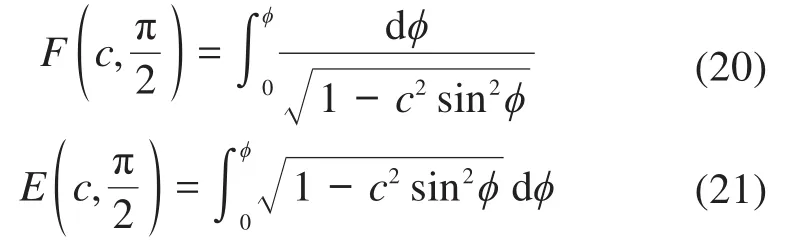
联立上述方程进行求解，当柔性梁对称变形并且当柔性短梁的初始角度为45°时，可以将高阶多项式拟合为图4所示的柔性长梁的载荷—位移曲线。

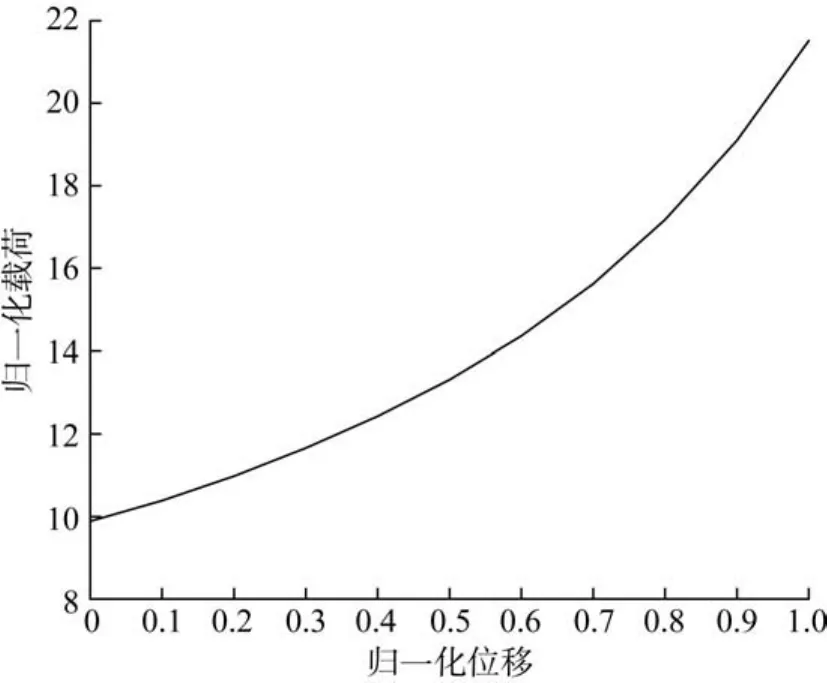
图4 柔性长梁的载荷—位移曲线Fig.4 Load-displacement curve of flexible long beam

同理可得柔性短梁的载荷—位移曲线。经过整理得到2根梁载荷—位移关系的表达式分别为：

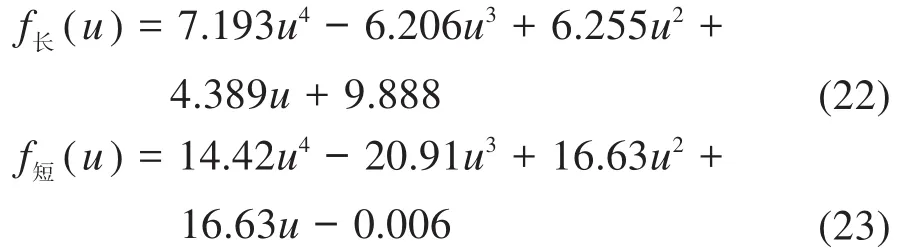
式中：u和f分别为归一化无量纲的位移和载荷：

式中：Δx=x-x′，为柔性梁在水平方向的变形量。

由于机构铰接的柔性梁以弹簧的形式储存和释放能量，所以2个柔性梁的运动模型都可以用具有相同载荷—位移特性的弹簧来代替，如图5所示。

图5 柔性梁的伪刚体模型Fig.5 Pseudo-rigid body model of flexible beam

公式（22）和（23）给出了2根柔性梁的载荷—位移关系式，则整理化简成等效非线性弹簧的轴向载荷FNL与位移x1的关系，得到：

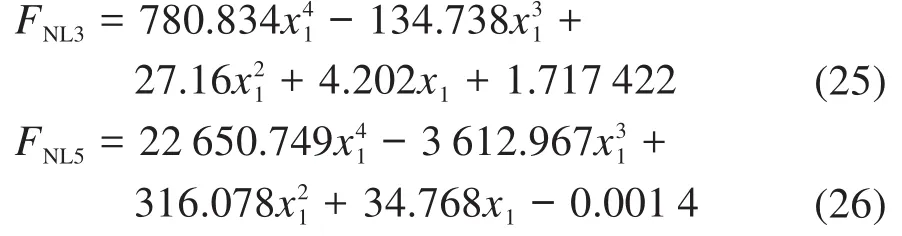
2 柔顺停歇机构运动学分析

2.1 柔顺停歇机构的伪刚体模型

假设滑块总保持与机架接触，其运动时的摩擦阻力可以忽略不计，且柔性片段在不变形时是直的。随着曲柄的旋转，曲柄的质心沿着预定的路径变化。根据上述分析可知，该柔顺停歇机构中2根柔性梁精确的运动学模型都可以等效为非线性平移弹簧，因此该柔顺停歇机构的整体伪刚体模型如图6所示。其中：θ3为伪刚体等效转角，即柔性长梁与水平方向的夹角；θ2为曲柄转角，曲柄与水平方向的夹角；θ5为短梁与水平方向的夹角。

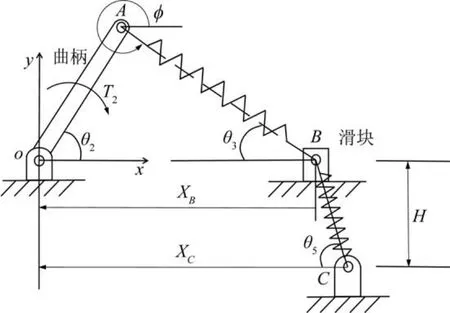
图6 柔顺停歇机构伪刚体模型Fig.6 Pseudo-rigid body model of compliant dwell mechanism

2.2 滑块的运动学方程

在整个运动过程中滑块的位置如图7所示。由于短梁的预加载作用，滑块只存在初始位置和右极限位置。滑块在初始位置时，设定θ2=180°，且顺时针旋转为正值，θ3=180°，θ5=45°，XC=350 mm，H=80 mm，且滑块的初始位置与电机支架的距离XB0=130 mm。

图7 滑块的位置Fig.7 Position analysis of the slider

运动过程中滑块的受力如图8所示。通过分析可知：

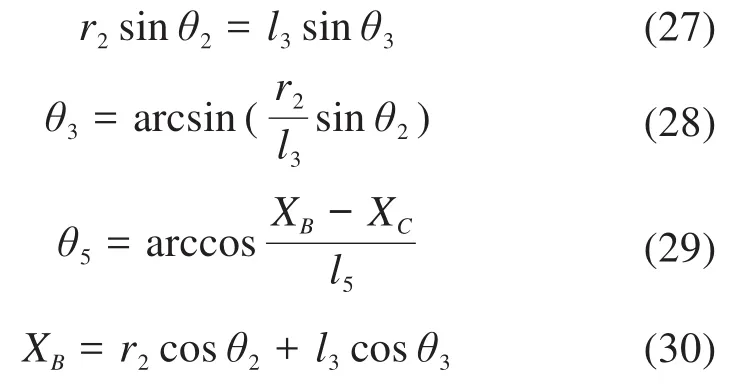
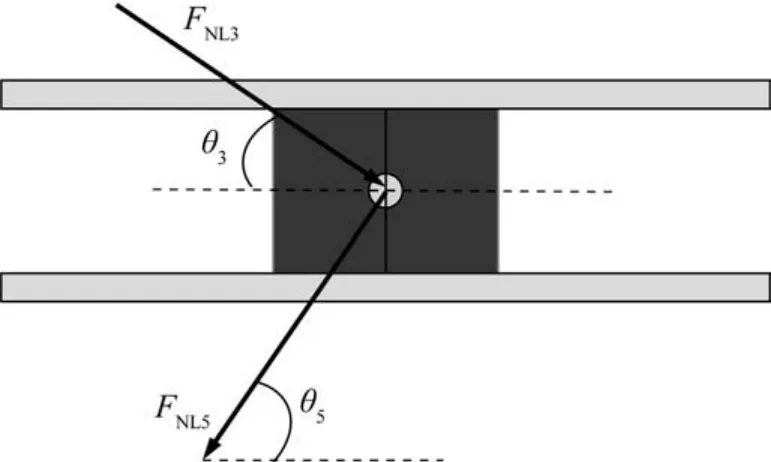
图8 滑块的受力Fig.8 Stress of the slider

滑块运动的位移xs为：

采用牛顿运动定律，由滑块的受力可知滑块的运动方程为：

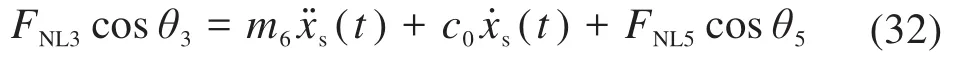
式中：c0为阻尼，在计算中取为0 N/（m/s）。

2.3 基于MATLAB/Simulink的求解与ADAMS验证

根据式（22）至式（32），建立以曲柄角为输入、滑块位移为输出的机构运动的数学模型，如图9所示。

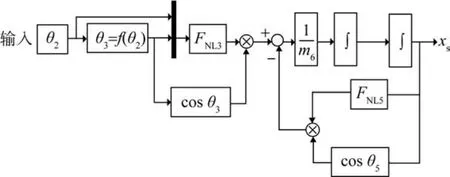
图9 以曲柄角为输入、滑块位移为输出的机构运动的数学模型Fig.9 Mathematical model of mechanism motion with crank angle as input and slider displacement as output

采用MATLAB/Simulink软件对该模型进行求解，来获得在任何给定曲柄转角下滑块的位移。该机构的停歇可以通过3个运动函数来表示：上升（向前运动）、停留（保持位置）和返回（向后运动）。采用四阶Runge Kutta微分求解器，以0.02 s的固定步长求解系统方程，持续12 s。输入表1所示的的机构参数，并以3 rad/s的角速度驱动曲柄，求解滑块位移随时间以及曲柄转角的变化曲线。

基于MATLAB/Simulink求解和ADAMS仿真得到的滑块位移随时间的变化曲线如图10所示。通过对比可以看到，ADAMS仿真结果与基于MATLAB/Simulink的求解结果基本吻合，证明机构运动的数学模型是正确的。由图可知，滑块最初保持静止，当短梁的预加载力达到长梁的临界屈曲载荷时，滑块快速运动直至右极限位置。在曲柄返回过程中，被压缩的短梁逐渐得到释放，其屈曲载荷逐渐减小到不再对长梁产生阻碍作用。在这个过程中，短梁由于释放前的翘曲，还会使滑块产生1次停顿，继而回到初始位置。该机构中，第2次停顿是瞬时的，因为水平力的微小变化会在后屈曲区域引起柔性梁相当大的位移。综上可知，该机构具有双停歇特性，在曲柄整个运动周期中存在1次精准停顿和1次瞬时停顿。

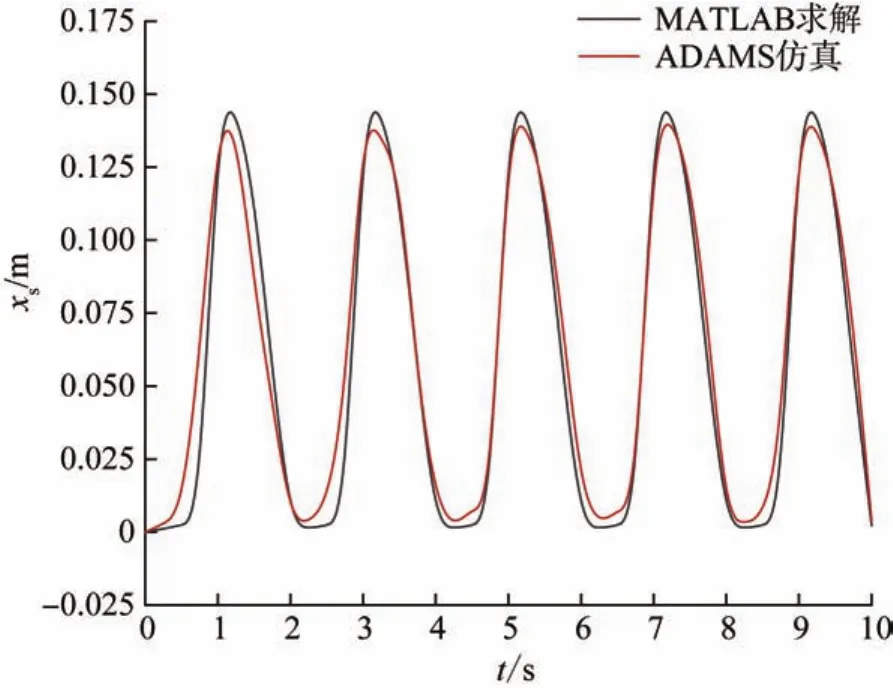
图10 滑块位移随时间的变化曲线Fig.10 Variation curve of slider displacement with time

滑块位移随曲柄转角的变化曲线如图11所示。由图可知，在曲柄整个运动周期中存在主要停歇区和次要停歇区两个不同的停歇区，主要停歇区是精准停歇区，次要停歇区是瞬时停歇区。机构的主要停顿出现在曲柄角为540°～630°之时，次要停顿出现在曲柄角为360°～400°之时，因此在曲柄一周360°的旋转中，机构停顿的对应角度约为130°，滑块停顿时间约为曲柄旋转1周所用时间的。

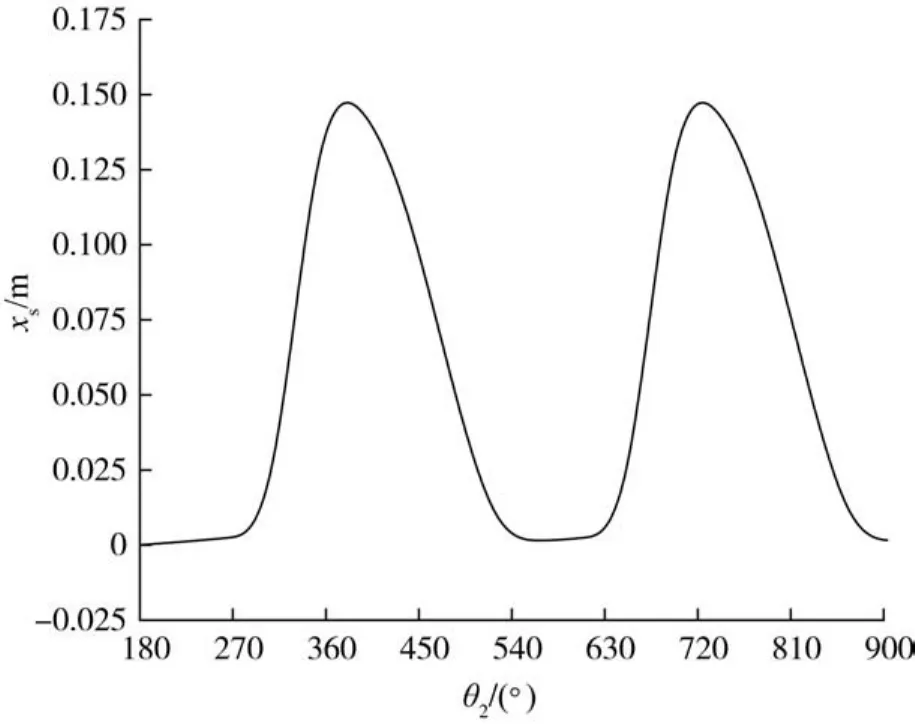
图11 滑块位移随曲柄转角的变化曲线Fig.11 Variation curve of slider displacement with crank angle

3 柔顺停歇机构频率特性分析

3.1 柔顺停歇机构的动力学方程

固有频率是评价机构内在特性的重要指标。下面通过推导柔顺停歇机构伪刚体模型的动力学方程来研究机构的固有频率特性。

3.1.1 动能分析

1）曲柄动能。

曲柄只存在绕支架的转动，所以只有转动动能。其转动动能T2可以表示为：

式中：J2为绕质心轴的的转动惯量，。

2）滑块的动能。

滑块动能T4为：

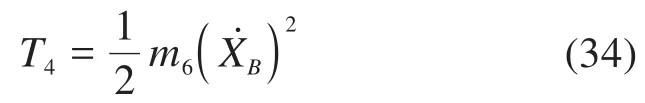
3.1.2 势能分析

柔性长梁的变形量Δx3为：

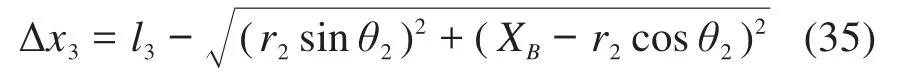
柔性短梁的变形量Δx5为：

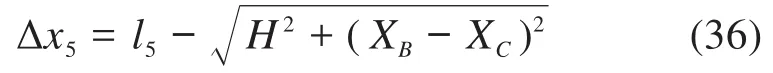
假设机构位于垂直于重力的平面内，则机构的势能为等效的弹簧势能。非线性弹簧的势能Ui（i=3，5）求解如下：

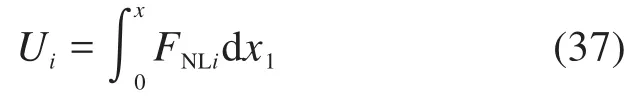
柔性长梁和短梁的轴向载荷可由式（25）和（26）求出，然后代入式（37）即可求得等其效非线性弹簧势能。

3.1.3 动力学方程

用Lagrange方程描述机构的数学模型为：

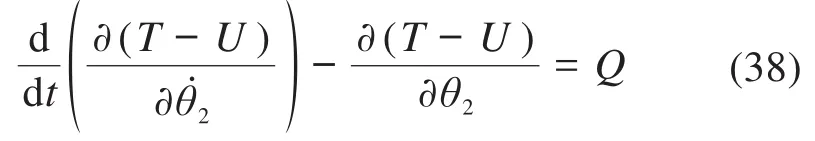
式中：T为机构总势能；U为机构总动能；Q为机构外在施加载荷。

由上述计算可知：

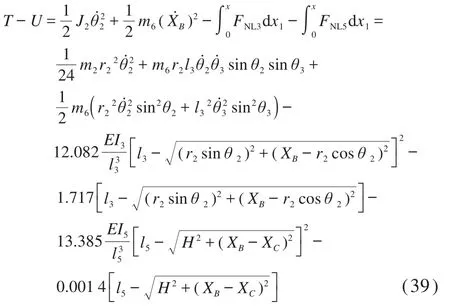
将式（39）代入式（38），可得：

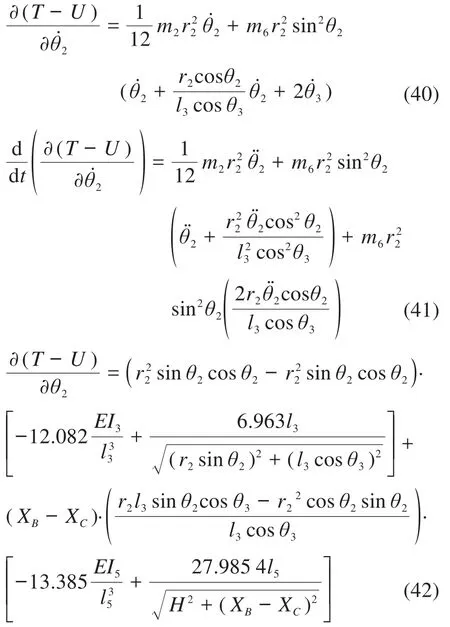
进一步整理式（42），得到只含有未知量θ2的表达式为：

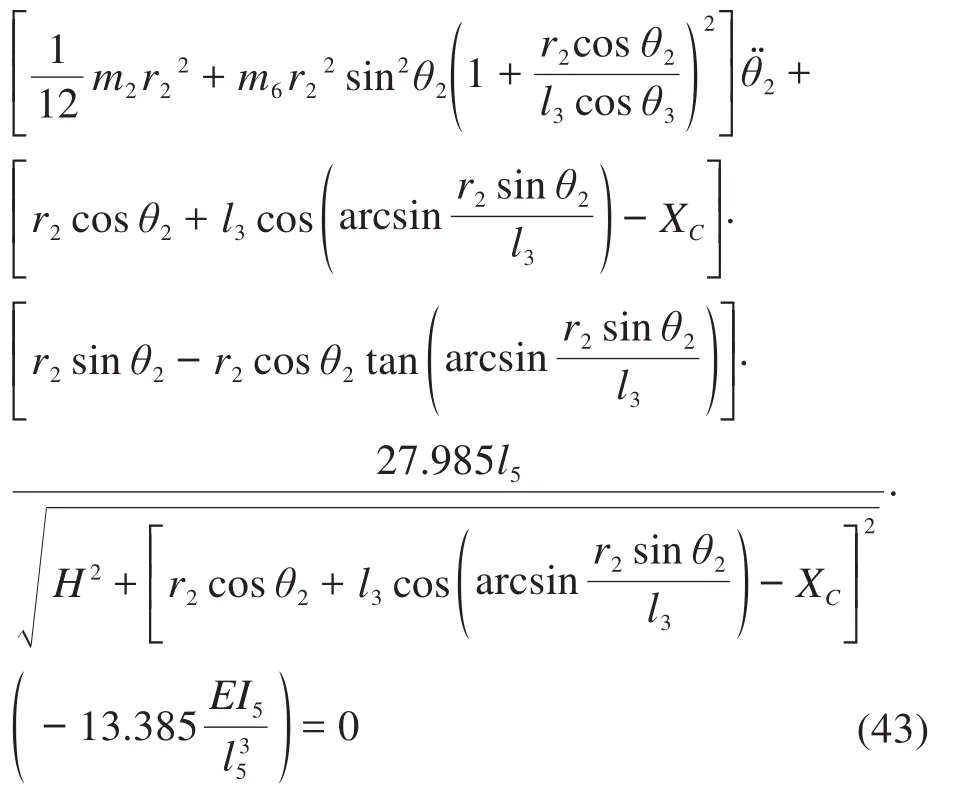
3.2 固有频率求解及分析

可以得出：

据此可以得到该柔顺停歇机构的固有频率特性为：

2）当机构的材料性能参数和柔性梁的长度固定时，ω∝h3，即固有频率与柔性长梁的截面厚度成正比。

4 柔顺停歇机构频率特性仿真

为了更直观、清晰地展现机构固有频率与各参数之间的关系，通过MATLAB软件进行仿真研究。

4.1 机构固有频率与柔性长梁截面参数的关系

机构共有2根柔性梁，根据式（43）可知机构固有频率只与柔性长梁的最小惯性矩有关，所以只改变柔性长梁的截面厚度h3，保持其他参数不变进行仿真。当h3=1.06，1.50，1.94，2.38，2.82，3.26 mm时，机构的固有频率如图12所示。由图可知，ω随着h3的增大而线性提高，表明ω与h3成正比的推论是正确的。

图12 柔性长梁截面厚度对机构固有频率的影响Fig.12 Influence of section thickness of flexible long beam on natural frequency of mechanism

只改变柔性长梁的截面宽度b3，保持其他参数不变。当b3的变化范围为20～30 mm时，机构的固有频率如图13所示。由图可知，ω随着b3的增大略有提高，但是提升的幅度非常小，说明ω基本不会随着b3的变化而变化。

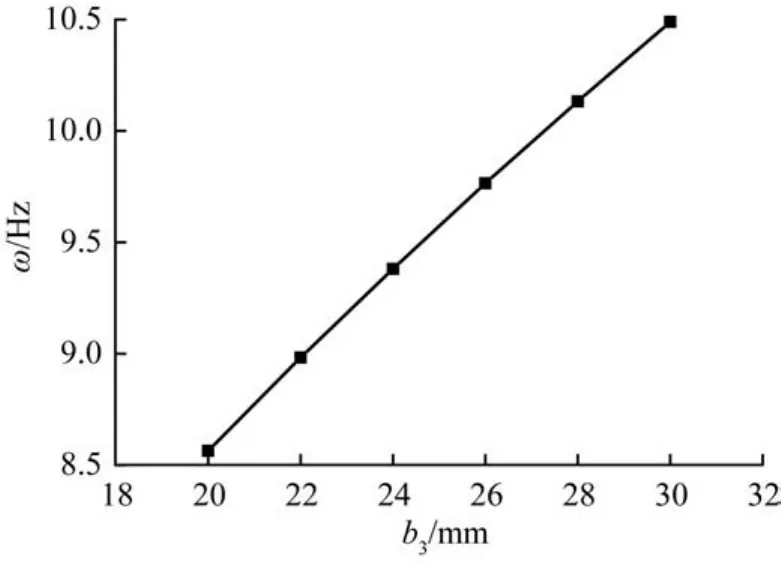
图13 柔性长梁截面宽度对机构固有频率的影响Fig.13 Influence of section width of flexible rod on natural frequency of mechanism

4.2 机构固有频率与柔性梁长度的关系

首先，只改变柔性长梁的长度l3，当l3的变化范围为200～300 mm时，机构的固有频率如图14所示。其次，只改变柔性短梁的长度l5，当l5的变化范围为110～220 mm时，机构的固有频率如图15所示。

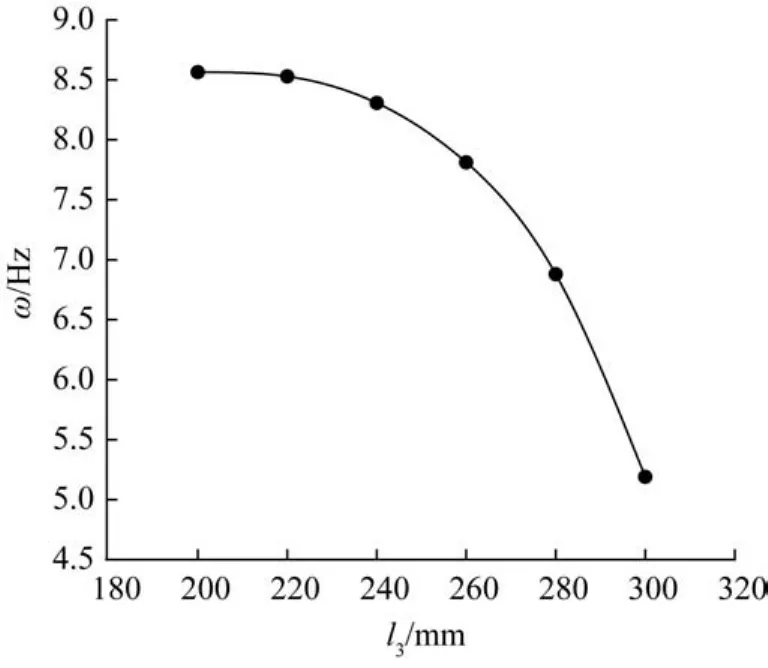
图14 柔性长梁长度对机构固有频率的影响Fig.14 Influence of length of flexible long beam on natural frequency of mechanism

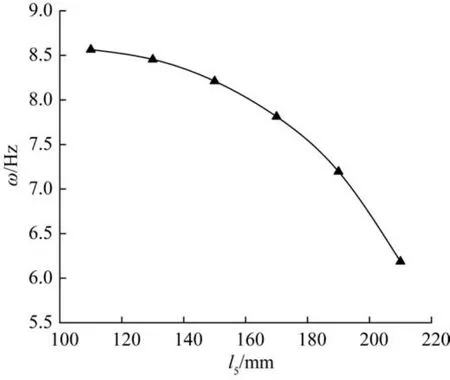
图15 柔性短梁长度对机构固有频率的影响Fig.15 Influence of the length of flexible short beam on natural frequency of mechanism

由图14、图15可知，系统固有频率随着梁长度的增大而迅速下降。因此，可以认为柔性梁越长，机构的柔度越大，而刚度的降低会造成梁的振动加大，这对机构控制及其对抗外部干扰很不利。

4.3 系统固有频率与材料性能参数的关系

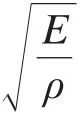
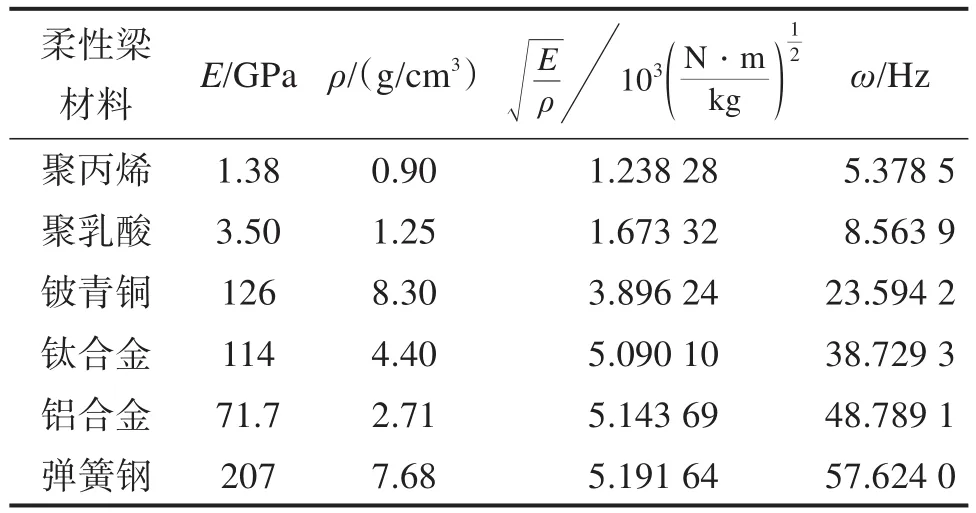
表2 选用不同柔性梁材料时机构的固有频率Table 2 Natural frequency of mechanism with different flexible beam materials

4.4 小结

不同的参数对机构固有频率的影响各不相同，因此，在柔顺停歇机构设计时要综合考虑各参数对机构力学特性的影响。

5 结论

1）通过屈曲分析将两端铰接的柔性梁等效为非线性弹簧，并求出其载荷—位移关系式，得到便于分析的机构运动学模型。采用MATLAB/Simulink软件求解得到滑块位移随时间及曲柄转角的变化曲线，并通过ADAMS仿真验证了理论计算的正确性。得到该停歇机构的运动特性：由于短梁预加载以及在运动过程中柔性梁的大变形，机构存在2次停顿。滑块停顿时间约为曲柄旋转1周所用时间的1/3，滑块位移达到最大值后存在短暂停顿。

2）基于机构伪刚体模型，建立了以柔性梁大变形为主要特征的柔顺停歇机构动力学模型，推导了只含变量θ2的变系数二阶系统动力学方程。求解并研究了柔顺停歇机构的固有频率特性，通过MATLAB仿真更直观地揭示了柔性长梁的截面参数、柔性梁长度和材料性能参数对机构固有频率的影响规律。不同的参数对机构固有频率的影响是不同的，因此，在柔顺停歇机构设计时要综合考虑各参数对机构力学特性的影响。这对柔顺停歇机构的设计及其进一步的动力学研究具有一定的指导意义。

3）将来须对平面连杆型柔顺停歇机构的工作性能进行进一步改善，使得停歇机构的结构更为紧凑、生产效率更高以及使用寿命更长，努力设计出结构简单、性能优良、方便分析的柔顺停歇机构，以减少机构的制造时间和成本。