曲柄摇杆机构的急回程度分析与探讨*
2021-02-07冯立艳梁会硕蔡玉强张雪雁崔冰艳李学刚李建功李德胜
冯立艳,梁会硕,蔡玉强,张雪雁,崔冰艳,李学刚,李建功,李德胜
(华北理工大学机械工程学院,河北 唐山 063210)
0 引言
当铰链四杆机构的最短杆与最长杆长度之和小于或等于其余两杆长度之和,且最短杆为连架杆时,则为曲柄摇杆机构。 曲柄摇杆机构能够实现曲柄整周转动与摆杆往复摆动之间的运动传递,有些场合,例如搅拌机、雷达天线俯仰搜索机构和颚式破碎机等,利用其急回特性可以缩短非工作时间,提高工作效率,同时生活中也出现了像空调的摆风机构、 电风扇的摇头机构等这种去程和回程都是工作行程的机器,所以对曲柄摇杆急回特性的研究很有必要。
1 极位夹角的探讨及急回运动分析
现在大多数的《机械原理》教材中对于极位夹角θ 的定义一般如下: 摇杆处于两极限位置时曲柄两对应位置所夹的锐角[1]。 然而,这并不准确,极位夹角的可能取值应是零度、锐角、直角和钝角。 在文献[2]中作出了明确定义:当从动件处于两个极限位置时,对应曲柄的一个位置与另一个位置的反向延长线间所夹的角度。
曲柄摇杆机构的四个杆长满足一定关系式时,极位夹角的取值可以在[0°,180°)之间[3],推导如下:
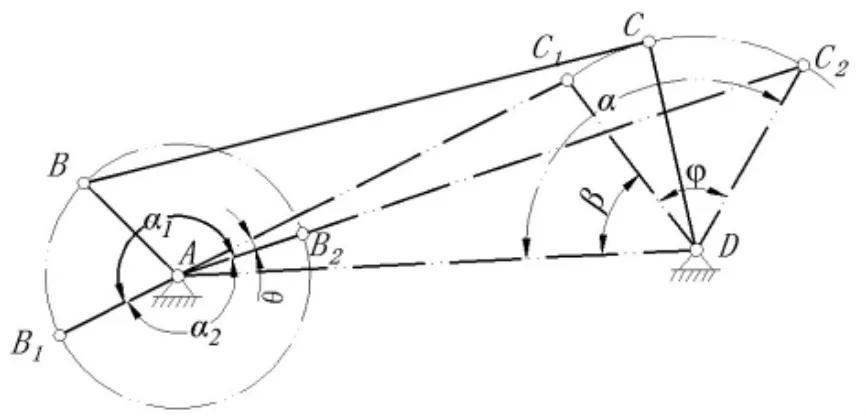
图1 曲柄摇杆机构
图1 中,曲柄 AB、连杆 BC、摇杆 CD 和机架 AD 的长度依次用 a、b、c、d 表示,φ 是摇杆的摆角,∠C1AC2为极位夹角。 令∠ADC2=α,∠ADC1=β,则 α=β+φ。
式(1)(2)(3)联立得,
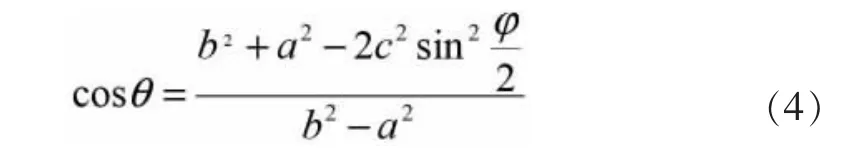
图1 所示机构具有急回特性,分析如下:当摇杆从左极限位置DC1运动到右极限位置DC2,再运动到DC1,即曲柄从AB1到AB2,再回到AB1的过程中,曲柄两个过程的角度相差2θ,所用的时间是不同的。 而摇杆转动的角度即摆角是相同的,所以导致摇杆两次摆动的角速度不相等。 亦即输出件的反行程快于它的正行程。
通常用行程速比系数K 来描述机构急回的程度,即

其中:极位夹角θ 等于零时,K=1,机构无急回;极位夹角θ不等于零时,K>1,且K 值越大,急回程度越大。
2 曲柄摇杆机构的分类及各自的杆长关系
曲柄摇杆机构可能无急回特性,也可能有急回特性,其中有急回特性的曲柄摇杆机构分为Ⅰ型和Ⅱ型两种。摇杆工作行程(慢行程)时的转向与曲柄转向相同时,称为Ⅰ型机构;反之,则称为Ⅱ型机构[4]。
Ⅰ型曲柄摇杆机构的特点是A、D 两点在C1C2直线的同侧;Ⅱ型机构的A、D 两点在C1C2直线的异侧[5]。
2.1 无急回特性的曲柄摇杆机构
极位夹角θ=0°,即摇杆CD 处于左右两极限位置时,此时 AB1C1和 AB2C2共线[6],如图 2 所示。
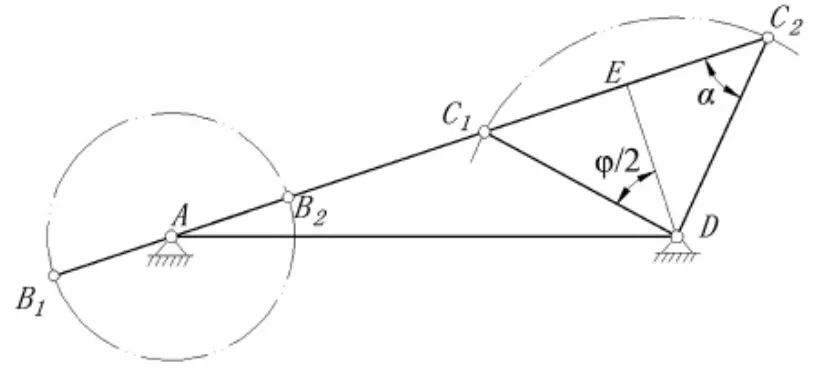
图2 无急回特性的曲柄摇杆机构
当 θ=0°,由图可知 E 点为 C1C2的中点,有

联立得,a2+ d2= b2+ c2,即无急回(K=1)的曲柄摇杆机构应满足的杆长关系。
2.2 Ⅰ型和Ⅱ型曲柄摇杆机构
因Ⅰ型曲柄摇杆机构的极位夹角θ 可能为锐角,也可能为钝角,故图3 绘出θ 为锐角、直角、钝角三种情况下摇杆的极限位置与对应的曲柄位置。 图中E、F 点为摇杆CD的两个极限位置或其延长线与圆的交点[7]。


图3 Ⅰ型曲柄摇杆机构
在△ADC1中,
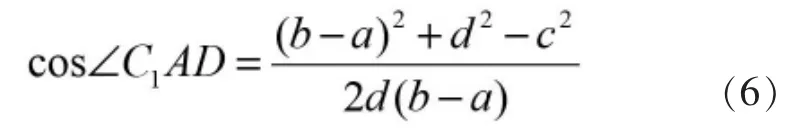
在△ADC2中,

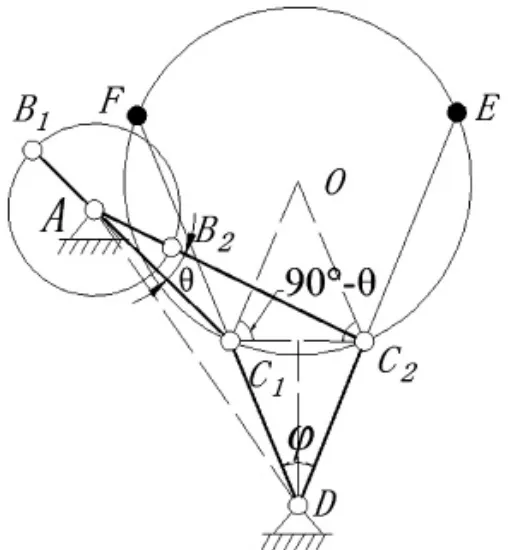
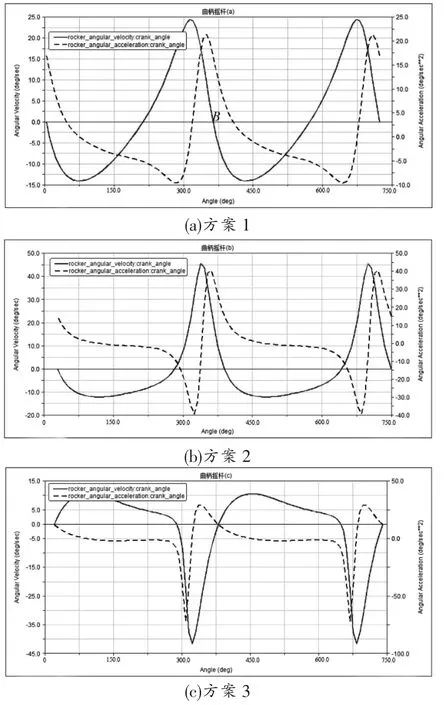
因Ⅰ型曲柄摇杆机构 (图 3a、b 和 c) 中∠C1AD>∠C2AD,则 cos∠C1AD 因Ⅱ型曲柄摇杆机构的∠C1AD<∠C2AD,则 cos∠C1AD>cos∠C2AD,联立式(6)和式(7)并化简,如图 4 所示,得Ⅱ型曲柄摇杆机构各杆长关系为: 图4 Ⅱ型曲柄摇杆机构 图5 最大极位夹角 如图3 所示,随着极位夹角θ 从锐角过渡到钝角,摇杆CD(或其延长线C1F、C2E)不断靠近圆的位置。 此时就会出现一个极限位置,即当摇杆CD 与圆O 相切,此时C1点和 F 点重合,C2点和 E 点重合,如图 5 所示,这种情况下的极位夹角θ 即是最大值[8]。 基于ADAMS 软件对上述各种情况的曲柄摇杆机构杆长条件进行了三维动画的制作及仿真,得以进一步验证。 表1 是Ⅰ型曲柄摇杆机构行程速比系数K 和φ 摇杆摆角三种不同取值下的杆长关系。 图6 是三种情况下的动画仿真截图,其中杆AB 为曲柄,杆BC 为连杆,杆CD为摇杆,杆AD 为机架。 表1 曲柄摇杆机构 (单位:mm) 图6 曲柄摇杆机构动画仿真 在ADAMS 中成功仿真之后,进行后处理。 以曲柄转角为横坐标,摇杆角速度和角加速度分别为纵坐标,得出如图7 的关系曲线图。 因曲柄AB 匀速转动,由图可知当摇杆角速度为正与负时,所对应曲柄转角的比值为行程速比系数K。 图7 曲柄摇杆的摇杆角速度、角加速度—曲柄转角的关系 通过三维动画的运行仿真以及曲线图,验证了上述研究理论。 1)文章探讨了极位夹角θ 的准确意义,分别推导出有无急回特性的曲柄摇杆机构的杆长关系。 2)推导出Ⅰ、Ⅱ型曲柄摇杆机构极位夹角θ 及行程速比系数K 的取值范围。 3)运用Adams 软件对Ⅰ型曲柄摇杆机构的三种极位夹角情况进行了验证。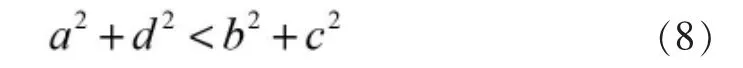

3 Ⅰ型和Ⅱ型曲柄摇杆机构极位夹角θ 和行程速比系数K 的最大值

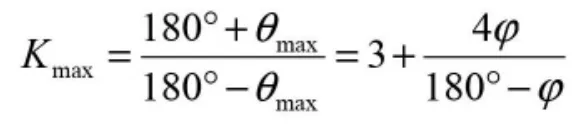

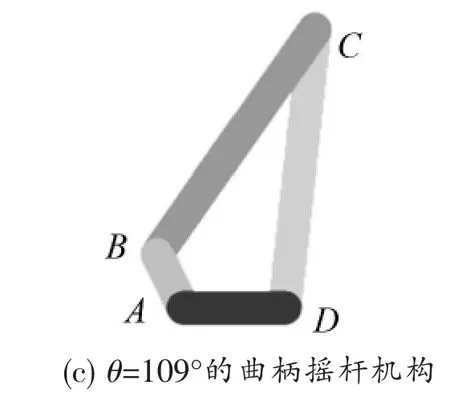
4 算例


5 结论
