4WID-4WIS智能车阿克曼转向轨迹规划及位置估算

2022-05-06时培成杨爱喜

工程设计学报 2022年2期

时培成，陈旭，杨爱喜，章亮

（1.安徽工程大学汽车新技术安徽省工程技术研究中心，安徽芜湖 241000；2.浙江大学工程师学院，浙江杭州 310000）

轨迹规划是智能车的基本功能之一，其目的是通过传感器感知周围环境并利用主动避障功能找到一条从起点到终点的最佳路径［1］。根据环境条件的不同，轨迹规划方法分为全局规划方法和局部规划方法。常用的全局规划方法有A*算法［2］、Dijkstra（狄克斯特拉）算法［3］和蚁群算法［4］等；常用的局部规划方法有多项式曲线法［5］、人工势场法［6］、贝塞尔曲线法［7］和B样条曲线法［8］等。其中，贝塞尔曲线具有曲率连续的优点，只需要确定控制点的坐标即可获得最优轨迹，其计算量较小，从而得到了广泛应用。张新锋等［9］基于贝塞尔曲线对智能商用车的换道避障轨迹进行了规划，并利用遗传算法选取最优避障路径，但是其在路径寻优中并未考虑遗传算法对参数寻优的随机性，且没有通过实车验证。陈成等［10］基于四阶贝塞尔曲线探讨了无人车轨迹规划的可行性，并推导了相应的曲率约束条件，同时利用序列二次规划（sequential quadratic programming,SQP）算法选取最优轨迹，但其在轨迹规划中对车辆的动力学约束不足。Jolly等［11］利用三阶贝塞尔曲线对机器人的轨迹规划问题进行了研究，但其提出的规划方法仅考虑了加速度约束，并未考虑曲率约束。高嵩等［12］针对无人车局部避障问题，基于贝塞尔曲线对无人车的避障路径进行了规划，其通过最小化曲线的曲率差值来选取曲线的控制点，并利用SQP算法选取最优避障路径，同时结合实际道路情况进行了避障仿真实验，但是其在规划避障路径时并未考虑无人车的速度规划问题，在仿真实验时也没有考虑整车实际行驶情况对避障路径的影响。

基于此，笔者针对四轮独立驱动与四轮独立转向（four-wheel independent drive and four-wheel independent steering,4WID-4WIS）智能车的转向行驶工况，在已知起点位置的情况下，给定终点位置和行驶方向，利用三阶贝塞尔曲线规划一系列轨迹，并采用优化函数获取满足智能车初始状态约束、目标状态约束和曲率连续约束且曲率差值最小的最优轨迹，使智能车按最优轨迹从起点移动到终点并保持给定的航向角。同时，提出一种位置估算算法，将轨迹微元近似（即将轨迹无限细分），以直线轨迹代替曲线轨迹，并利用惯性导航系统测量的航向角和编码器的脉冲数对智能车的位置进行估算。

1 基于三阶贝塞尔曲线的智能车轨迹规划

1.1 三阶贝塞尔曲线

贝塞尔曲线是法国工程师Bézier提出的一种适用于二维图形应用程序的数学曲线［13］。贝塞尔曲线由一组控制点确定：将给定的控制点按顺序连接构成多边形，通过调整控制点的坐标来改变贝塞尔曲线的形状，使曲线不断逼近该多边形。对于由n+1个控制点P0、P1、P2、…、Pn（其位置矢量分别为P0、P1、P2、…、Pn）确定的贝塞尔曲线，定义为：

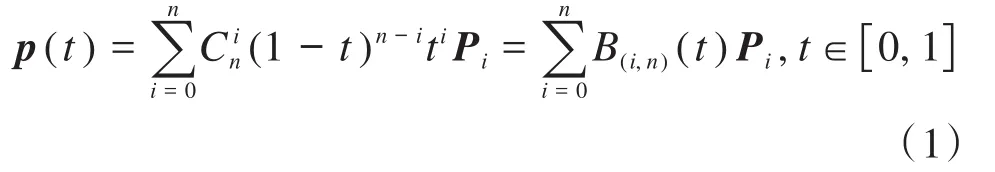
式中：B(i，n)(t)为伯恩斯坦基函数［14］；t为比例，其决定了贝塞尔曲线组成点的数量。

鉴于本文基于三阶贝塞尔曲线对4WID-4WIS智能车的阿克曼转向轨迹进行规划，则仅对该曲线的相关特性进行介绍。图1所示为由4个控制点P0、P1、P2和P3唯一确定的三阶贝塞尔曲线，依次连接4个控制点可得到3条一阶贝塞尔曲线，分别为P0P1、P1P2和P2P3。

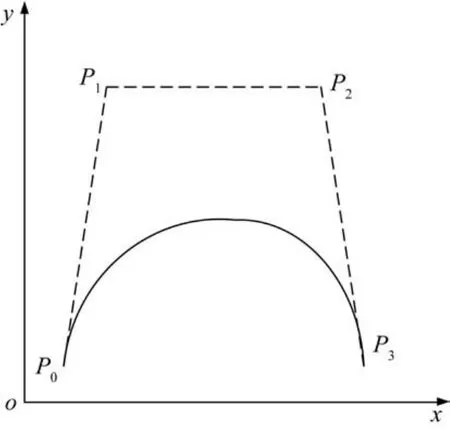
图1 三阶贝塞尔曲线示意Fig.1 Schematic diagram of third-order Bézier curve

三阶贝塞尔曲线的性质［15］如下：

1）曲线的参数化表达式为：

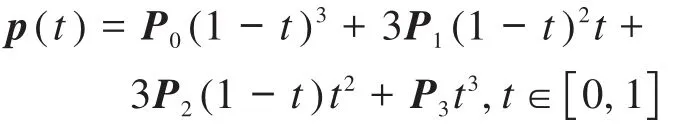
2）曲线经过两端的控制点：

p(0)=P0，p(1)=P3

3）起点和终点分别为曲线两端的切点，切向量为：

p′(0)=3(P1-P0)，p′(1)=3(P3-P2)

1.2 轨迹规划

针对4WID-4WIS智能车在阿克曼转向工况下进行曲线行驶时，已知起点A，即第1个控制点P0的坐标为(X0，Y0，β0)，其中X0、Y0分别为起点A的横、纵坐标，β0为起点A处的航向角；终点B，即第4个控制点P3的坐标为(X3，Y3，β3)，各变量的含义同上。基于三阶贝塞尔曲线规划轨迹，使智能车从起点A移动到指定的终点B，规划的轨迹如图2所示。

图2 基于三阶贝塞尔曲线的智能车轨迹规划示意Fig.2 Schematic diagram of intelligent vehicle trajectory planning based on third-order Bézier curve

根据三阶贝塞尔曲线的定义可知，该规划轨迹由3条一阶贝塞尔曲线和4个控制点确定，第1条一阶贝塞尔曲线为控制点P0、P1的连线P0P1，第2条一阶贝塞尔曲线为控制点P1、P2的连线P1P2，第3条一阶贝塞尔曲线为控制点P2、P3的连线P2P3。延长P0P1和P2P3相交于O点，则控制点P1可以取直线AO上的任意一点，但不与A点和O点重合；控制点P2可以取直线BO上的任意一点，但不与B点和O点重合。

由控制点P0的坐标可得，第1条一阶贝塞尔曲线P0P1的方程为：

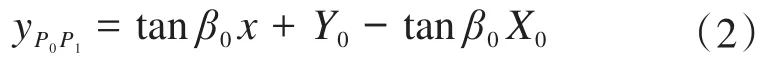
由控制点P3的坐标可得，第3条一阶贝塞尔曲线P2P3的方程为：

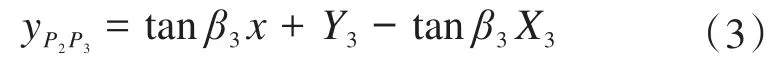
联立式（2）和式（3）可得，一阶贝塞尔曲线P0P1和P2P3的交点O的横、纵坐标XO、YO分别为：

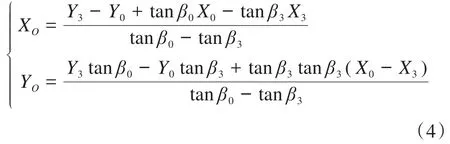
由此可得，控制点P1的横、纵坐标X1、Y1的取值范围为：

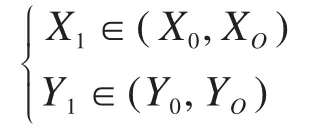
控制点P2的横、纵坐标X2、Y2的取值范围为：

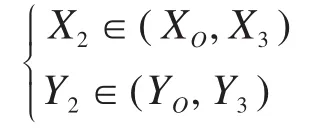
通过以上方法，固定三阶贝塞尔曲线的控制点P0、P3，在直线AO和BO上分别选择2个点作为控制点P1和P2，即可获得满足智能车初始状态约束、目标状态约束以及曲率连续约束的一系列轨迹。

1.3 轨迹优化求解

本文采用最优函数来求解满足上述约束条件的最优参数，从而获得最优轨迹。所构建的优化函数为J(P1,P2)：

式中：t1、t2分别为三阶贝塞尔曲线达到最大曲率与最小曲率时t的取值。

函数J（P1，P2）的含义为：通过优化控制点P1和P2来使所规划轨迹的最大曲率与最小曲率的差值最小，即其曲率变化最小，从而使轨迹更加平滑，以便车辆平顺、稳定地行驶［16］。

2 智能车轨迹规划仿真验证

在4WID-4WIS智能车阿克曼转向轨迹规划中，首先要确定其初始位姿和目标位姿，然后根据上文方法进行轨迹规划，最后在所规划的一系列轨迹中选择1条最为平滑的轨迹，即最优轨迹。本文以4WID-4WIS智能车的初始位置为坐标系原点，此时航向角为0°，即车身与x轴平行，则其初始位姿为（0 m，0 m，0°）；目标位置的坐标为（20，30）m，航向角为90°，即车身与y轴平行，则目标位姿为（20 m，30 m，90°）；所规划轨迹由200个点组成。通过在MATLAB软件中编程规划得到从起点（0，0）m到终点（20，30）m的一系列轨迹，并在这些轨迹中选择最大曲率与最小曲率差值最小的一条轨迹作为最优轨迹。

1）给定控制点P1坐标，控制点P2坐标寻优。

固定控制点P1的坐标，由智能车在起点处的航向角为0°可确定P1的坐标为(10，0)m；由智能车在终点处的航向角为90°可确定控制点P2的横坐标为20 m。通过改变P2的纵坐标规划得到30条不同的轨迹，结果如图3所示。其中：图3（a）所示为规划得到的30条轨迹；图3（b）所示为每条规划轨迹的最大曲率与最小曲率的差值变化情况；图3（c）所示为最优轨迹，即第9条规划轨迹。

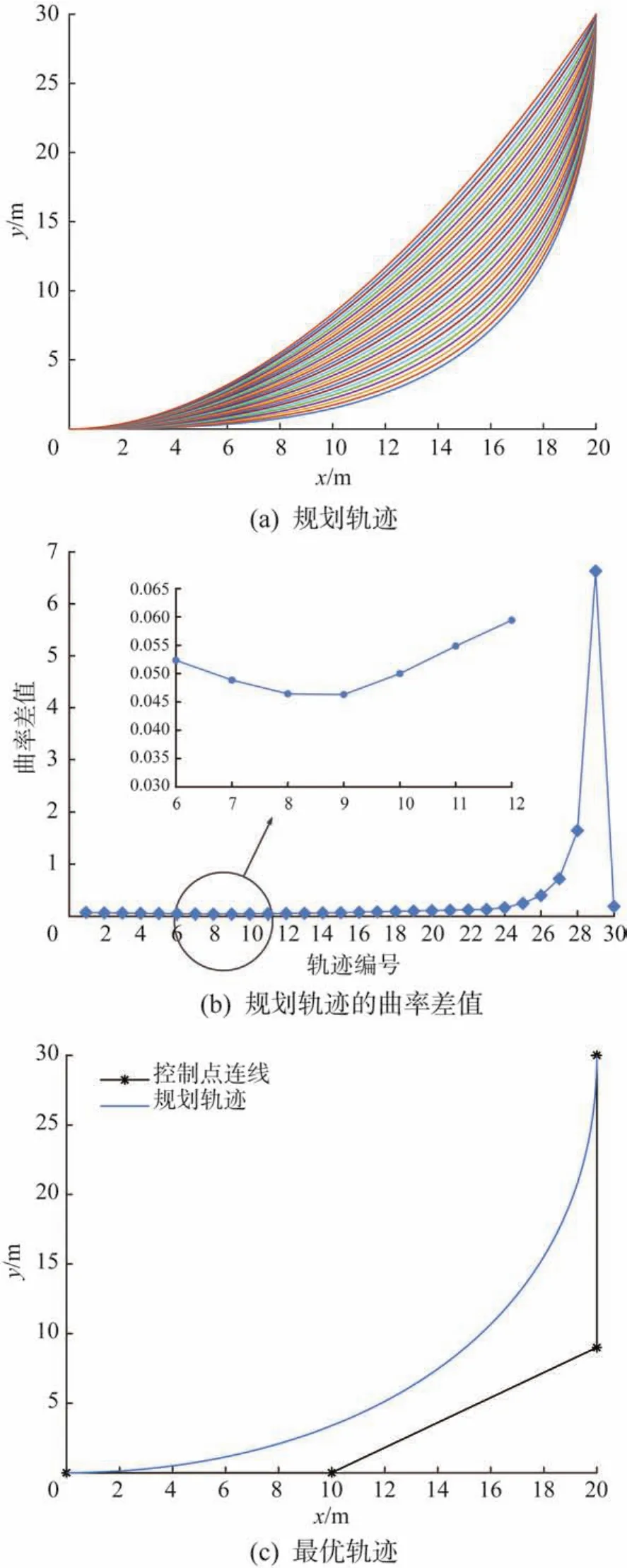
图3 改变控制点P2所得的4WID-4WIS智能车轨迹规划仿真结果Fig.3 Trajectory planning simulation results of 4WID-4WIS intelligent vehicle obtained by changing control pointP2

由图3可以得出，第9条规划轨迹的最大曲率与最小曲率的差值最小，为0.046 3，则该轨迹即为最优轨迹，此时控制点P2的纵坐标为8 m。由此可得，4个控制点P0、P1、P2和P3的坐标分别为(0，0)，(10，0)，(20，9)和(20，30)m。

2）给定控制点P2坐标，控制点P1坐标寻优。

固定控制点P2的坐标，由智能车在终点处的航向角为90°可确定控制点P2的坐标为(20，15)m；由智能车在起点处的航向角为0°可知，控制点P1的纵坐标为0 m。通过改变P1的横坐标规划得到20条不同的轨迹，结果如图4所示。其中：图4（a）所示为规划得到的20条轨迹；图4（b）所示为每条轨迹的最大曲率与最小曲率的差值变化情况；图4（c）所示为最优轨迹，即第13条轨迹。

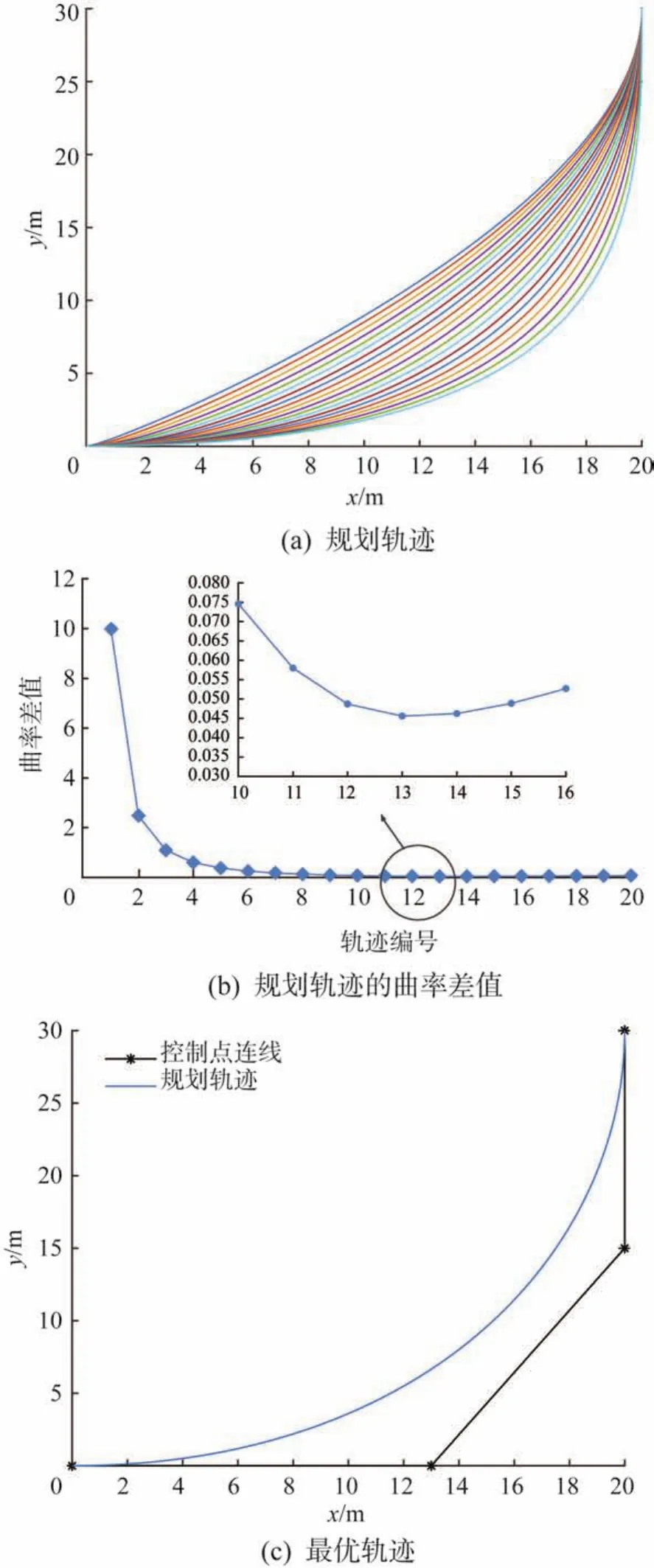
图4 改变控制点P1所得的4WID-4WIS智能车轨迹规划仿真结果Fig.4 Trajectory planning simulation results of 4WID-4WIS intelligent vehicle obtained by changing control pointP1

由图4可以得出，第13条规划轨迹的最大曲率与最小曲率的差值最小，为0.045 6，则该轨迹即为最优轨迹，此时控制点P1的横坐标为13 m。由此可得，4个控制点P0、P1、P2和P3的坐标分别为(0，0)，(13，0)，(20，15)和(20，30)m。

3）控制点P1、P2坐标同时寻优。

由上述结果可知，仅改变控制点P1或P2的坐标，无法真正得到最优轨迹，这是因为只改变一个点的坐标有可能会漏掉曲率差值真正最小的曲线。因此，应按照上文所述方法，通过同时改变控制点P1的横坐标和控制点P2的纵坐标来寻找真正的最优轨迹。通过同时改变控制点P1、P2的坐标规划得到600条不同的轨迹，结果如图5所示。其中：图5（a）所示为规划得到的600条轨迹；图5（b）所示为每条规划轨迹的最大曲率与最小曲率的差值变化情况；图5（c）所示为最优轨迹，即第406条轨迹。

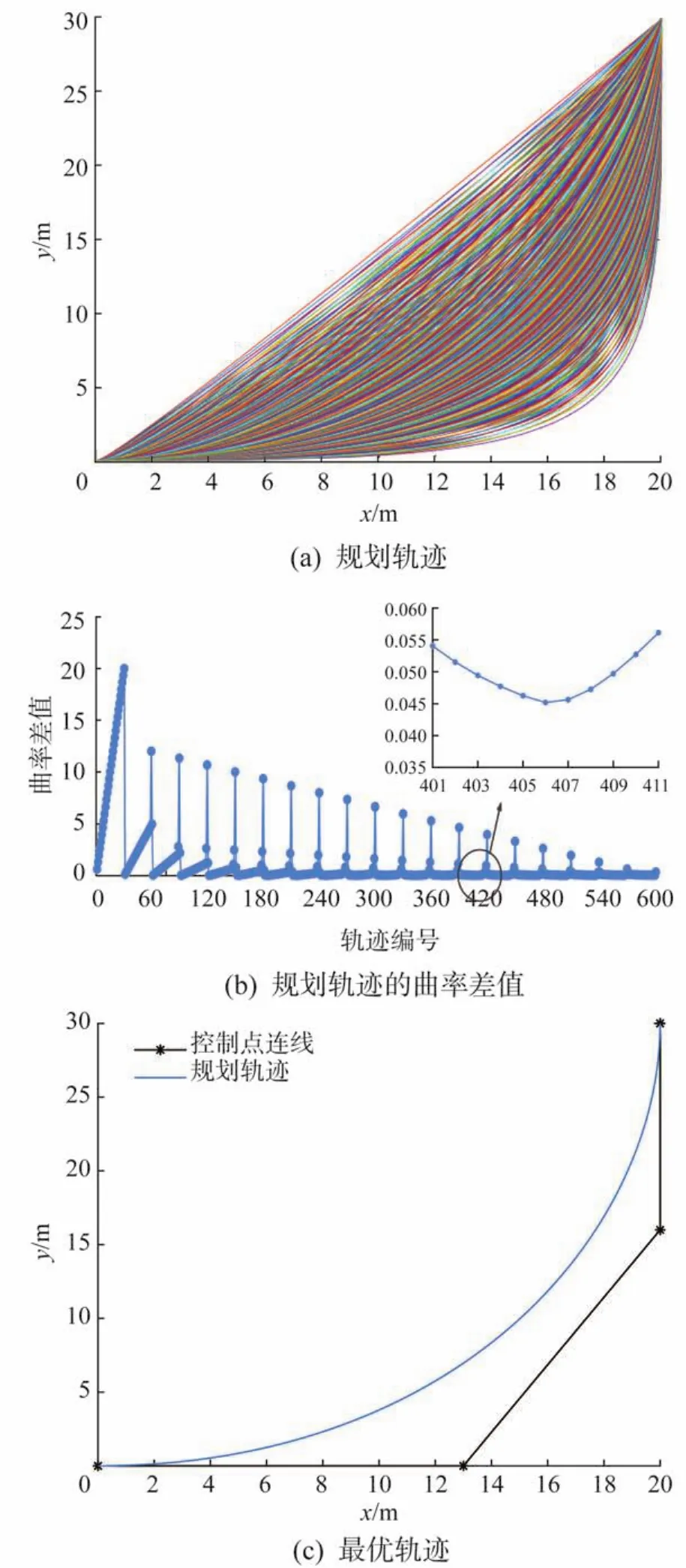
图5 同时改变控制点P1、P2所得的4WID-4WIS智能车轨迹规划仿真结果Fig.5 Simulation results of trajectory planning of 4WID-4WIS intelligent vehicle obtained by changing control pointP1andP2at the same time

由图5可以得出，第406条规划轨迹的最大曲率与最小曲率的差值最小，为0.045 2，则该轨迹即为最优轨迹，此时控制点P1的横坐标为13 m，控制点P2的纵坐标为16 m。由此可得，4个控制点P0、P1、P2和P3的坐标分别为(0，0)，(13，0)，(20，16)和(20，30)m。

基于不同寻优方式获得的智能车最优轨迹控制点的仿真结果如表1所示。由表中数据可知，仅对控制点P1的横坐标或控制点P2的纵坐标进行寻优，无法获得曲率差值真正最小的最优轨迹，须同时对控制点P1的横坐标和控制点P2的纵坐标进行寻优，才能得到满足约束条件的最优轨迹。

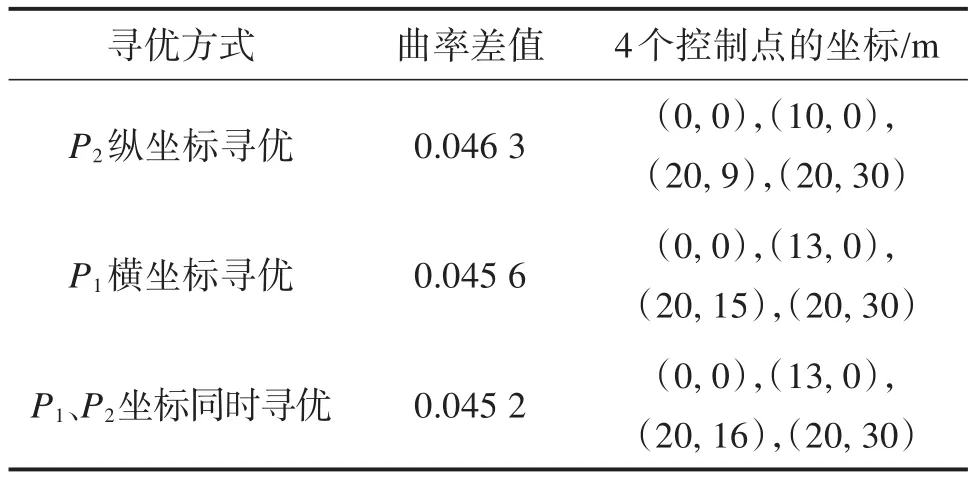
表1 4WID-4WIS智能车最优轨迹控制点仿真结果对比Table 1 Comparison of simulation results of optimal trajectory control points of 4WID-4WIS intelligent vehicle

3 智能车位置估算算法

3.1 算法简介

在智能车运行时，需要对其位置进行估算，以便实时掌握其运行姿态。常用定位算法通常采用惯性导航系统和编码器来测量数据。如：文献［17］针对轮式机器人，提出了一种改进的轨迹推算方法，即通过编码器测定2个同轴驱动轮的速度，从而建立一种新的轨迹推算理论模型，以尽可能去除外部干扰，提高定位精度，但该方法只是改变了推算模型，并未解决使用单一编码器误差较大的问题。文献［18］通过测量差动驱动机器人的2个同轴驱动轮的角速度，并利用其差动驱动系统的运动规律推算驱动轮在下一个采样时刻的位置，但该方法仅仅在理论上进行了推导，并未通过机器人的实际行驶情况来验证理论模型的正确性。为此，笔者提出了一种基于惯性导航系统和编码器的4WID-4WIS智能车位置估算算法。首先，在根据比例t划分的每小段轨迹内，通过惯性导航系统测量获得智能车航向角的变化量，并利用编码器记录4个驱动电机的脉冲数，根据航向角的变化量和编码器的脉冲数来计算智能车中心点的转弯半径；然后，根据中心点转弯半径和航向角变化量，计算该段轨迹内智能车的转向弧长；最后，将转向弧线分段近似为线段，并计算各段轨迹的长度，同时根据各段轨迹的长度和航向角的变化量，计算智能车的位置增量，实现其位置估算。

3.2 阿克曼转向模型

4WID-4WIS智能车的阿克曼转向模型（左转）如图6所示。图中：H为整车转向中心，D为左、右侧驱动轮轮距，W为前后驱动轮轴距，R为整车中心点转弯半径，R1为左侧驱动轮转弯半径，Rr为右侧驱动轮转弯半径，δl为左侧驱动轮转角，δr为右侧驱动轮转角。

当4WID-4WIS智能车运行时，利用其驱动轮上编码器的脉冲数和惯性导航系统测量的航向角来估算其位姿。设编码器旋转一周的脉冲数为N，在每小段轨迹内，惯性导航系统测量得到的航向角变化量为dθ，编码器的脉冲数为M，则有：

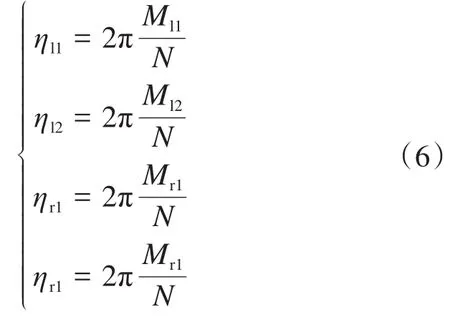
式中：ηl1、ηl2、ηr1和ηr1为智能车运行时左、右侧前后驱动轮的滚动角度；Ml1、Ml2、Mr1和Mr1为左、右侧前后驱动轮上编码器的脉冲数。

由左、右侧前后2个驱动轮的转弯半径相同可知：

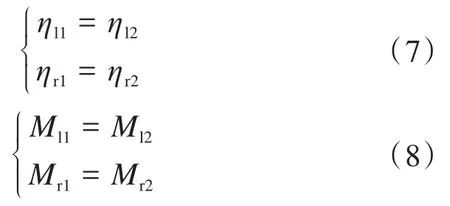
在实际运行过程中，因驱动轮的加工材质不完全相同导致不同驱动轮与地面的摩擦不同［19］，以及硬件上的干扰信号导致编码器返回值受影响等因素，同侧驱动轮上编码器的脉冲数也可能不同。为了防止因驱动轮打滑而造成的编码器脉冲数的增加，本文取同侧编码器中较小的脉冲数，同时在运行过程中观察脉冲数的变化，若发现脉冲数增加明显，则说明侧滑现象严重，应重新进行分析。

由此可得，左、右侧驱动轮的行驶距离Sl、Sr分别为：

式中：ηl、ηr为左、右侧驱动轮的滚动角度；Rwheel为驱动轮半径。

则左、右侧驱动轮的转弯半径Rl、Rr分别为：

基于左、右侧驱动轮转弯半径计算得到的整车中心点转弯半径R1、R2，分别为：

由于存在不可抗力的影响因素，基于左、右侧驱动轮转弯半径求得的整车中心点转弯半径可能不同，本文取二者的平均值，即：

3.3 位置增量计算

对于轮式智能车来说，传统的轨迹推算过程是将曲线路径进行微元近似，即把曲线无限细分，并将每一小段路径近似成线段进行计算，所有线段距离加和值即为拟合的曲线长度［20］，其原理如图7所示。

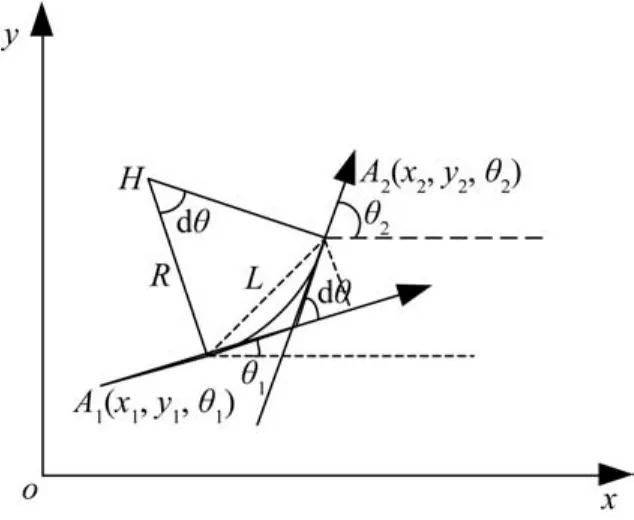
图7 4WID-4WIS智能车轨迹推算原理Fig.7 Calculation principle of trajectory of 4WID-4WIS intelligent vehicle

如图7所示，假设4WID-4WIS智能车沿着圆弧形轨迹从起点A1(x1，y1，θ1)运行到终点A2(x2，y2，θ2)，其中θ1、θ2分别为智能车在点A1和A2处的航向角，dθ为点A2相对于点A1的航向角变化量，即：

根据智能车中心点转弯半径和该段轨迹内航向角的变化量，计算得到该段轨迹的长度lA1A2为：

将长度为lA1A2的圆弧近似为长度为L的线段进行计算，由图7可得：

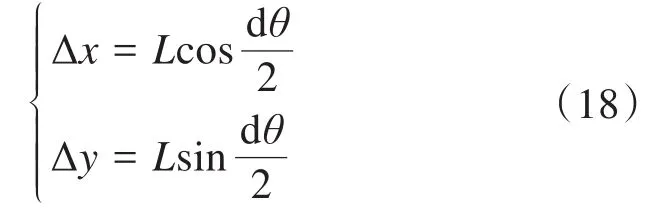
则可推算出终点A2处智能车的位姿为：

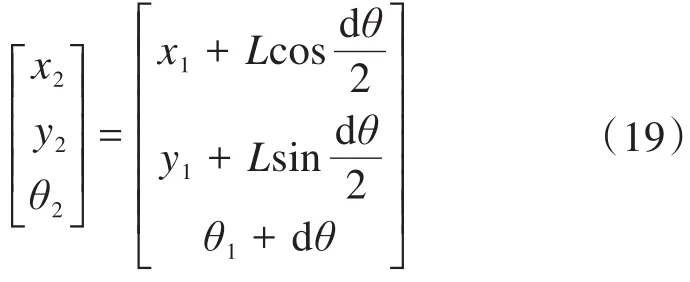
4 试验验证

为了验证所提出的轨迹规划方法以及位置估算算法的可行性，在实车试验平台开展相关试验。试验中4WID-4WIS智能车的初始位姿和目标位姿与仿真时一致，即分别为（0 m，0 m，0°）和（20 m，30 m，90°）。同时，为了避免智能车运行时四轮驱动和四轮转向相互干涉影响，在硬件设计上，设置主控制板通过控制器局域网（controller area network，CAN）与电机驱动器进行通信：通过CANA与驱动电机驱动器通信，通过CANB与转向电机驱动器通信，以保证驱动和转向在控制上相互独立。在软件设计上，驱动电机在速度环、电流环模式下工作，主控制板通过发送目标速度、电流来控制驱动电机；转向电机在位置环模式下工作，主控制板通过发送目标位置来控制转向电机，以避免驱动和转向在工作时相互影响。试验用4WID-4WIS智能车实物如图8所示。

图8 4WID-4WIS智能车实物Fig.8 Physical object of 4WID-4WIS intelligent vehicle

试验用4WID-4WIS智能车采用DSP28335芯片作为主控芯片，惯性导航系统为格纳微公司生产的GNW-SurPass-A100航姿参考系统，驱动电机（实车上为轮毂电机）编码器为增量式编码器。该智能车的具体参数如表2所示。

表2 4WID-4WIS智能车的参数Table 2 Parameters of 4WID-4WIS intelligent vehicle

在起点处对4WID-4WIS智能车发送目标位姿指令，其主控制器根据轨迹规划算法选取最优轨迹并控制智能车根据规划轨迹从起点运行到终点。在运行过程中，利用惯性导航系统测量智能车的航向角变化量，并读取增量式编码器的脉冲数，试验数据如图9所示。

图9 4WID-4WIS智能车运行过程中的航向角和脉冲数Fig.9 Navigation angle and pulse number of 4WID-4WIS intelligent vehicle during driving

由图9（a）可知，4WID-4WIS智能车在初始位置处保持设定的航向角0°，在按照规划轨迹运行时，其航向角不断变化，到达目标位置时，由于地面摩擦力以及轮胎打滑等因素的影响，其最终的航向角为89.876°，与给定航向角90°的误差为0.13%。由图9（b）可知，在划分的每段轨迹内，脉冲数越多，说明智能车的运行轨迹长度越长；脉冲数越少，说明智能车的运行轨迹长度越短。根据编码器的总脉冲数（本实验中为110 050），即可推算智能车的总运行轨迹长度。

根据4WID-4WIS智能车运行时惯性导航系统测量的航向角以及编码器的脉冲数，利用所提出的位置估算算法对智能车轨迹进行推算，并与规划规迹进行对比，结果如图10所示。

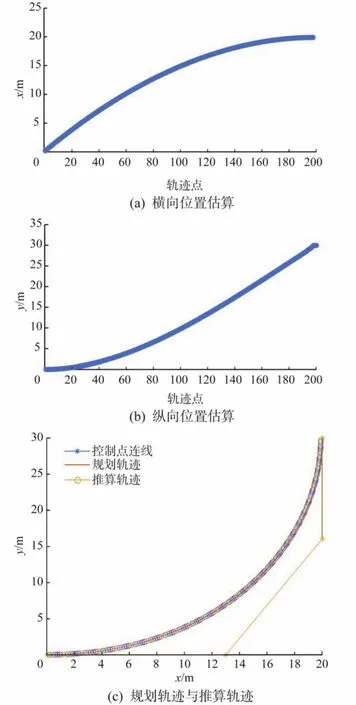
图10 4WID-4WIS智能车轨迹推算结果Fig.10 Calculation results of trajectory of4WID-4WIS intelligent vehicle

由图10（a）和图10（b）可得，估算得到的终点坐标为（19.962，29.941）m，与给定的终点坐标（20，30）m相比，横向位置的相对误差为0.19%，纵向位置的相对误差为0.20%。由图10（c）可以看出，推算轨迹与规划轨迹基本吻合，通过计算得到推算轨迹的长度为39.698 m，与规划轨迹长度39.785 m的相对误差为0.22%。