三角混合两级杠杆微位移放大机构的设计及性能分析

丰 飞，傅雨晨，范 伟，马 举

（1.龙岩技师学院，福建 龙岩 364000；2.华侨大学机电及自动化学院，福建 厦门 361021）

随着微纳驱动、微机电控制驱动等技术的迅猛发展，高精度的微纳驱动定位平台［1-3］被广泛应用于微生物操作台、高精度加工台和光学快速反射镜等［4-8］。其中，压电陶瓷作为微纳驱动定位平台的核心部件，其输出位移不足几十微米，存在一定的局限性。随着对微位移放大机构性能要求的提高，有必要研制新型的微位移放大机构来对位移进行放大并传输［9-11］。基于柔性铰链的微位移放大机构能够产生较大的输出位移，因此受到了国内外学者的广泛关注［12-15］。倪迎雪等［16］研究了一种新型混合柔性铰链的柔度，为该柔性铰链的设计和优化提供了理论依据。余跃庆等［17］设计了一种高精度的大变形柔性铰链，通过仿真和试验发现，用X形柔性铰链替代传统的刚性转动副可以较大程度地提高并联机器人的运动精度和综合性能。张法业等［18］将柔性铰链结构应用于光纤光栅加速度传感器，大大提高了传感器的横向抗扰能力和灵敏度。Choi等［19］基于直圆形柔性铰链设计和优化了一种对称式位移放大机构。根据红外光谱仪动镜支撑机构高精度、高带宽的要求［20］，张明月等［21］采用平行簧片结构设计了一种动镜柔性支撑机构。Wang等［22］基于直圆形柔性铰链设计了一种三级混合式位移放大机构并应用于微夹钳，大大增大了微夹钳的夹持行程。

为了解决微位移放大机构铰链单一、位移放大倍数偏小等缺陷，同时为了满足压电驱动系统高精度、大行程的输出要求，笔者设计了一种三角混合两级杠杆微位移放大机构。首先，推导了微位移放大机构的位移放大公式和放大比；其次，对两级杠杆中支点铰链的类型进行仿真对比，分析直圆形、直梁形、直圆长形铰链对输入载荷的敏感性；然后，利用有限元分析软件进行微位移放大机构静力学和动力学仿真，将位移放大比的仿真值与理论值进行对比，来验证理论推导的正确性；最后，对微位移放大机构的相对寄生运动比和固定频率进行计算和仿真，来验证机构设计的合理性和有效性。

1 三角混合两级杠杆微位移放大机构的设计

1.1 机构的结构设计及工作原理

三角混合两级杠杆微位移放大机构的结构如图1所示。其主要由三角结构、两级杠杆结构、定位板、压电执行器和若干定位销组成。其中：2个三角结构左右对称分布，有利于提高位移放大倍数和输出应力；压电执行器放置在2个三角结构的正中间，其输出端紧紧贴合两侧三角结构的输入端。

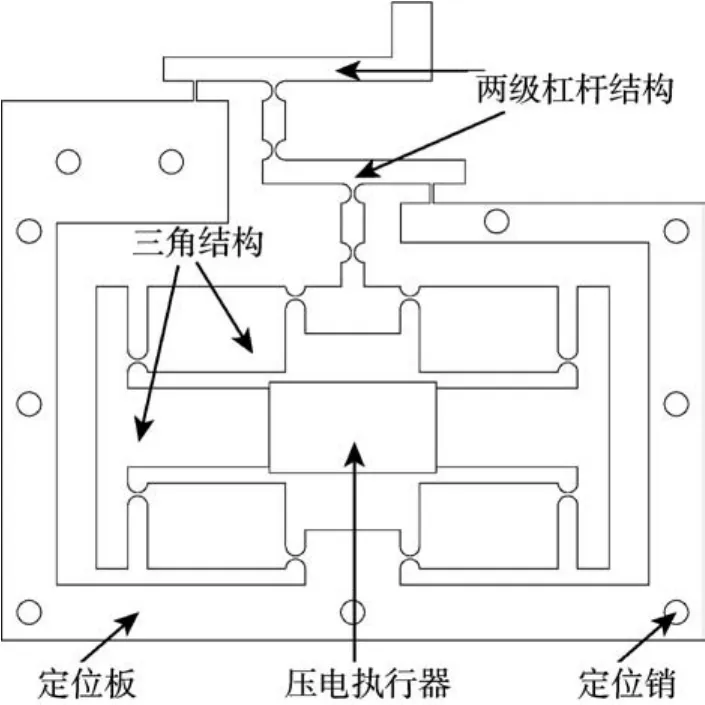
图1 三角混合两级杠杆微位移放大机构的结构Fig.1 Structure of triangular hybrid two-stage lever micro-displacement amplification mechanism

机构的工作原理如图2所示。当压电执行器的输入位移Δx对称作用在输入端2—3和12—13时，分别由1—2—3—4和11—12—13—14组成的三角结构对Δx进行第1次放大；三角结构的输出端4—11与一级杠杆的输入端5直接连接，所以一级杠杆的输入位移近似为三角结构的输出位移，则Δx经过一级杠杆10—5—6的第2次放大；输出端6即为二级杠杆的输入端7，Δx经过二级杠杆8—7—9的第3次放大，最终在杠杆结构末端9输出位移ΔY。

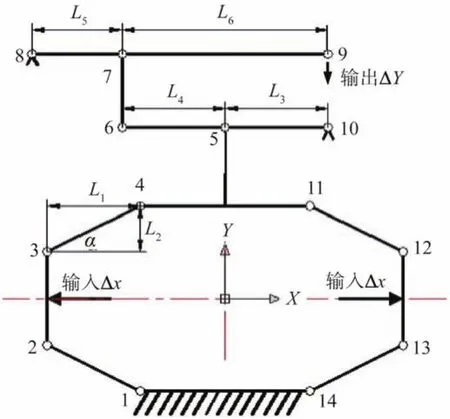
图2 三角混合两级杠杆微位移放大机构工作原理示意Fig.2 Schematic of working principle of triangular hybrid two-stage lever micro-displacement amplification mechanism

一级杠杆的输入端与三角结构的输出端直接相连，大大减小了机构的能量损失和位移损失。机构的这种组合方式虽然不能保证去除非必要的寄生位移，但是可以在较小的结构尺寸下得到较大的位移放大比，将输入位移完成近似90°的转向放大。

1.2 机构参数分析

三角结构和两级杠杆结构的工作原理如图3所示。当压电执行器对三角结构对称输入2个大小相同、方向相反的水平位移Δx后，会在其输出端输出一个垂直方向的位移Δy，三角结构中的夹角α随之减小为α-θ，其中θ为铰链的弯曲角度。

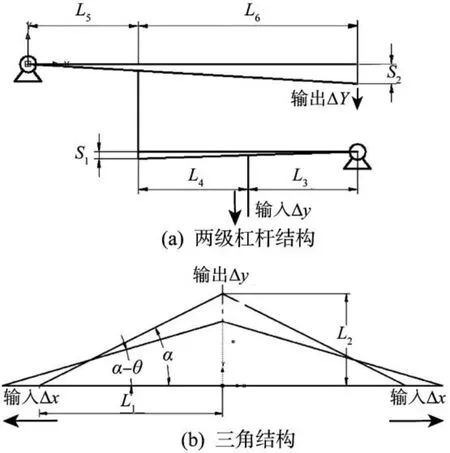
图3 三角结构和两级杠杆结构工作原理示意Fig.3 Schematic of working principle of triangular structure and two-stage lever structure

由图3可知：

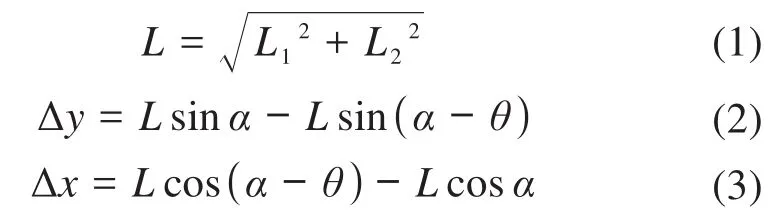
式中：L1为上部三角结构中2个铰链之间的横向距离，L2为上部三角结构中2个铰链之间的纵向距离；L为2个铰链之间的距离。

则三角结构的放大倍数K为：

由于柔性铰链的弯曲变形较小，可以忽略铰链弯曲变形带来的位移变化，因此θ≈0°。根据等价无穷小法则，得：sinθ≈θ，，则式（4）为：

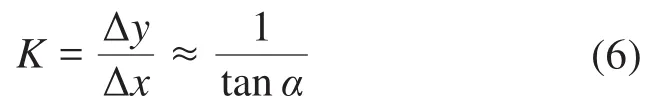
所设计的三角结构沿中心线上下对称，且下部三角结构与固定板直接相连。根据叠加定理，可得三角结构的总放大比K'为：

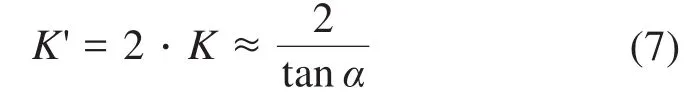
针对两级杠杆结构，定义2L3=2L4=2L5=L6，其中：L3为一级杠杆输入点与支点铰链之间的距离；L4为一级杠杆输出点与支点铰链之间的距离；L5为二级杠杆输入点与支点铰链之间的距离；L6为二级杠杆输出点与支点铰链之间的距离。则：

这是林书豪的综艺导师首秀。其他导师一边看选手激烈对决，一边“插科打诨”制造笑料，林书豪却专注着挑人。遇到实力派球员，他会送上一件代表晋级的球衣，即使面对发挥失常的选手，他也愿意“违反规则”，多给对方一次炫球技的机会。

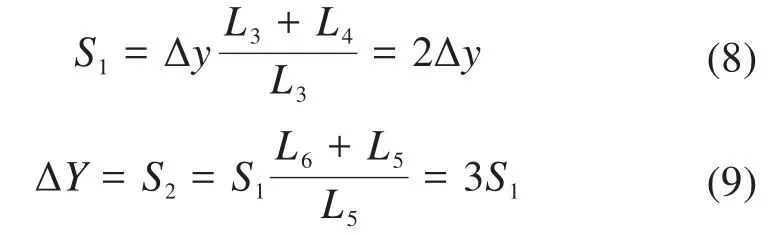
式中：S1为一级杠杆的输出位移；S2为二级杠杆的输出位移。

因此，二级杠杆结构的放大倍数K''为：

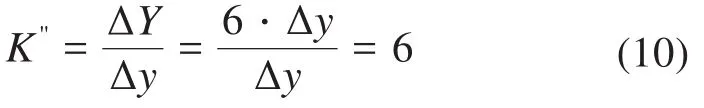
同时，由于三角结构的输出端直接与两级杠杆结构的输入端相连，则微位移放大机构的总放大倍数K理为：

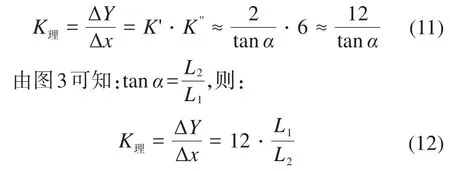
所设计的三角混合两级杠杆微位移放大机构的结构参数如表1所示。其中：t为直圆形铰链的中心厚度；R为直圆形铰链的切口半径；d为直圆形和直梁形铰链的切口长度。

表1 三角混合两级杠杆微位移放大机构的结构参数Table 1 Structural parameters of triangular hybrid twostage lever micro-displacement amplification mechanism 单位：mm

将L1、L2的值代入式（12），可得该微位移放大机构的理论总位移放大比为30.000。

1.3 两级杠杆支点铰链的对比分析

对两级杠杆支点的铰链类型进行对比分析，以找到对输入载荷具有更强敏感性的铰链结构。根据表1的铰链参数值，选择3种应用最广泛的铰链结构，分别为直圆形、直圆长形和直梁形铰链。铰链材料为锰钢，其密度为7 800 kg/m3，杨氏模量为210 GPa，泊松比为0.30，屈服极限为784 MPa。利用ANSYS软件对采用上述3种支点铰链的两级杠杆机构进行不同输入载荷下最大应力、最大输出位移的有限元分析，仿真结果如表2所示。其中，当输入载荷为2.0 MPa时，机构最大应力和最大输出位移如图4所示。

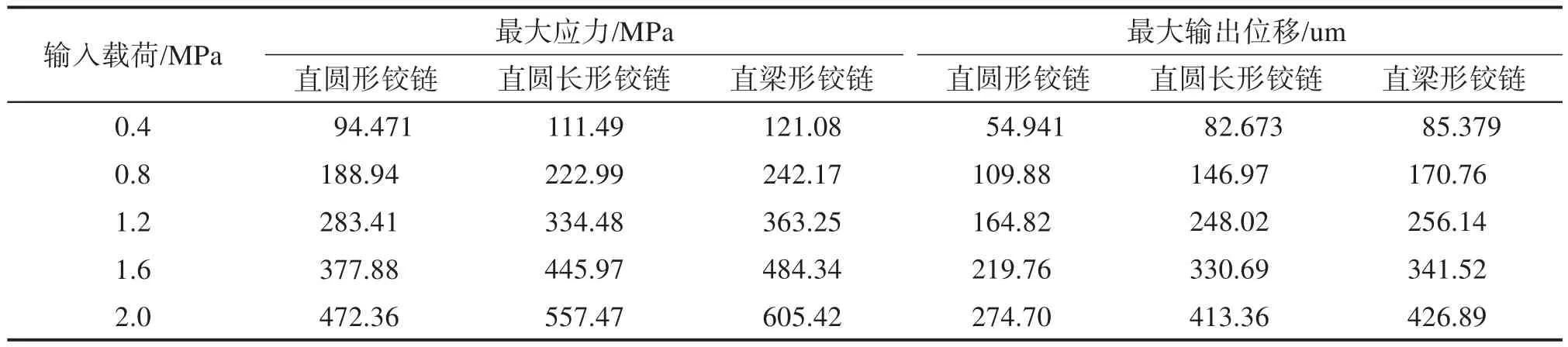
表2 三角混合两级杠杆微位移放大机构在不同输入载荷下最大应力、最大输出位移的有限元仿真结果Table 2 Finite element simulation results of maximum stress and maximum output displacement of triangular hybrid two-stage lever micro-displacement amplification mechanism under different input loads

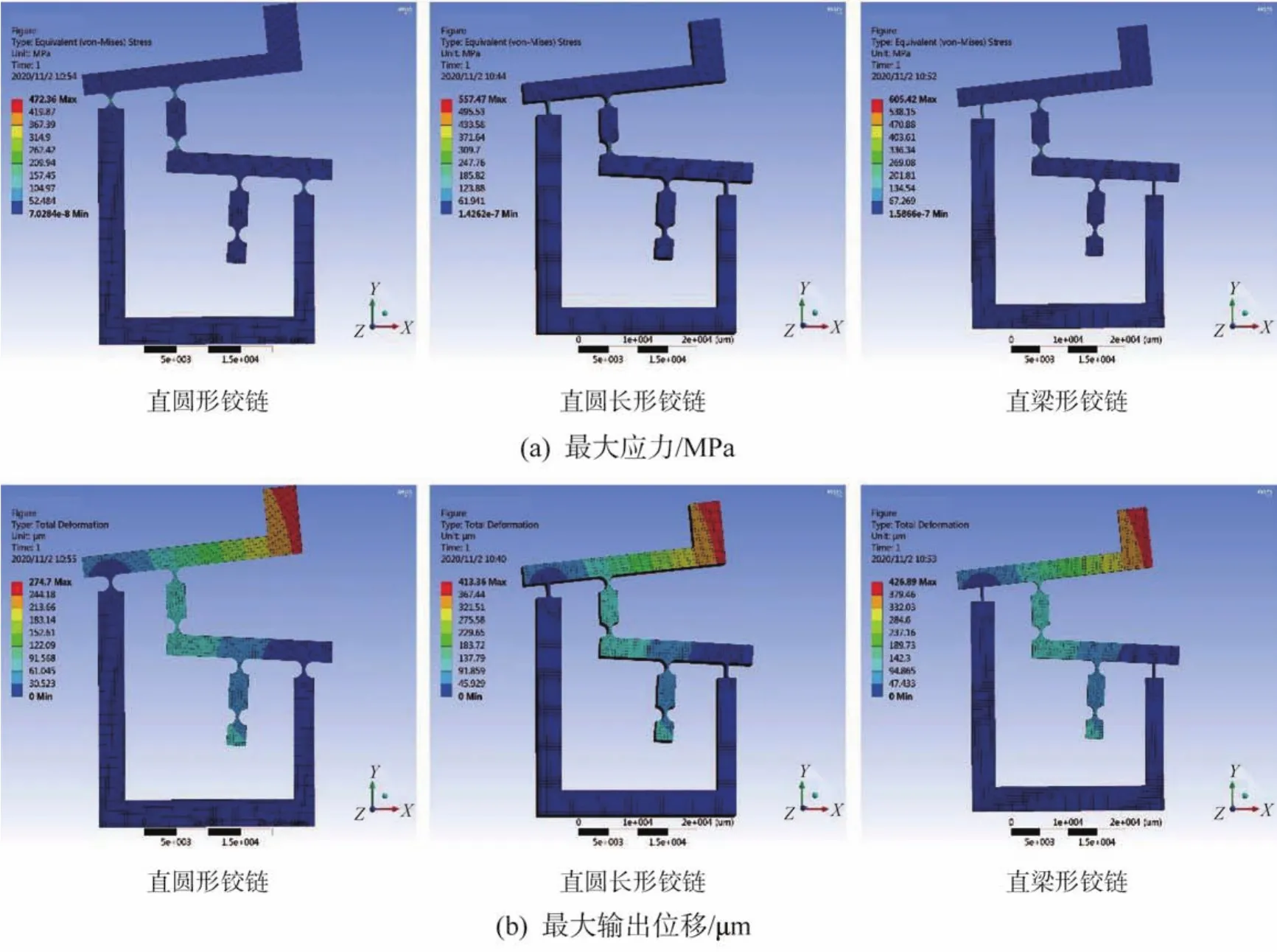
图4 输入载荷为2.0 MPa时三角混合两级杠杆微位移放大机构的最大应力和最大输出位移Fig.4 Maximum stress and maximum output displacement of triangular hybrid two-stage lever micro-displacement amplification mechanism with input load of 20 MPa

由表2和图4可知：两级杠杆机构的最大应力均出现在铰链结构中厚度最小的中心处；同时，随着输入载荷的增大，支点铰链的类型会对机构的输出位移产生一定的影响。其中，采用直圆形铰链的机构在不同输入载荷下的最大应力和最大输出位移均是最小的，当输入载荷为2.0 MPa载荷时，其最大应力仅为472.36 MPa，而采用其他2种铰链的机构的最大应力也没有超过锰钢的屈服极限。采用直圆长形和直梁形铰链的机构的最大位移分别是采用直圆形铰链机构的1.505倍和1.554倍，说明在满足屈服极限的前提下，直圆长形和直梁形铰链对输入载荷的敏感性更强。此外，随着输入载荷的增大，各最大应力和最大输出位移之间的差值越来越大。为了得到最佳的位移放大效果，采用敏感性更强的直梁形铰链作为两级杠杆结构的支点铰链。

2 三角混合两级杠杆微位移放大机构的静力学和动力学仿真

2.1 静力学仿真

为了验证三角混合两级杠杆微位移机构的结构合理性，对机构进行静力学仿真。在Solidworks软件中建立机构的三维实体模型，在其定位板上设置若干定位销，使机构尽可能在X、Y两个方向产生位移；机构的结构参数设置如表1，机构的厚度为8 mm，铰链材料的设置与理论分析时相同。采用ANSYS软件对机构模型进行网格划分，网格大小为2 000 μm，并设定压电执行器的输出位移为20 μm，即Δx=10 μm；对机构的应力和总输出位移进行有限元仿真，仿真结果如图5所示。

图5 Δx=10 μm时三角混合两级杠杆微位移放大机构的应力云图和总输出位移Fig.5 Stress nephogram and total output displacement of triangular hybrid two-stage lever micro-displacement amplification mechanism when Δx=10 μm

由图5（a）可知，当输入位移为10 μm时，机构的最大应力出现在二级杠杆的支点铰链处，为383.95 MPa，且小于锰钢的屈服极限。因此，所设计的微位移放大机构在形变的过程中受到的应力不会超过屈服极限，不会发生断裂。同时可以看到，由于机构中三角结构对称设置，三角结构的应力也近似呈对称分布，从而保证了机构的稳定性，有利于机构的运行。

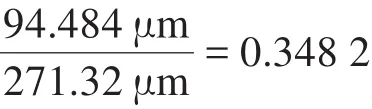
2.2 动力学仿真

通过对微位移放大机构的静力学仿真，可以分析机构在一定输入位移下的静态响应，而动力学仿真则用来评价机构的动态性能。其常用的评价指标有固有频率、转动刚度和转动应力等，其中固有频率对机构的驱动控制精度和动态响应能力有较大的影响。利用ANSYS软件进行机构固有频率的动力学仿真。取前6阶模态进行分析，参数设置同上。机构前6阶模态及对应的固有频率如图6和表3所示。

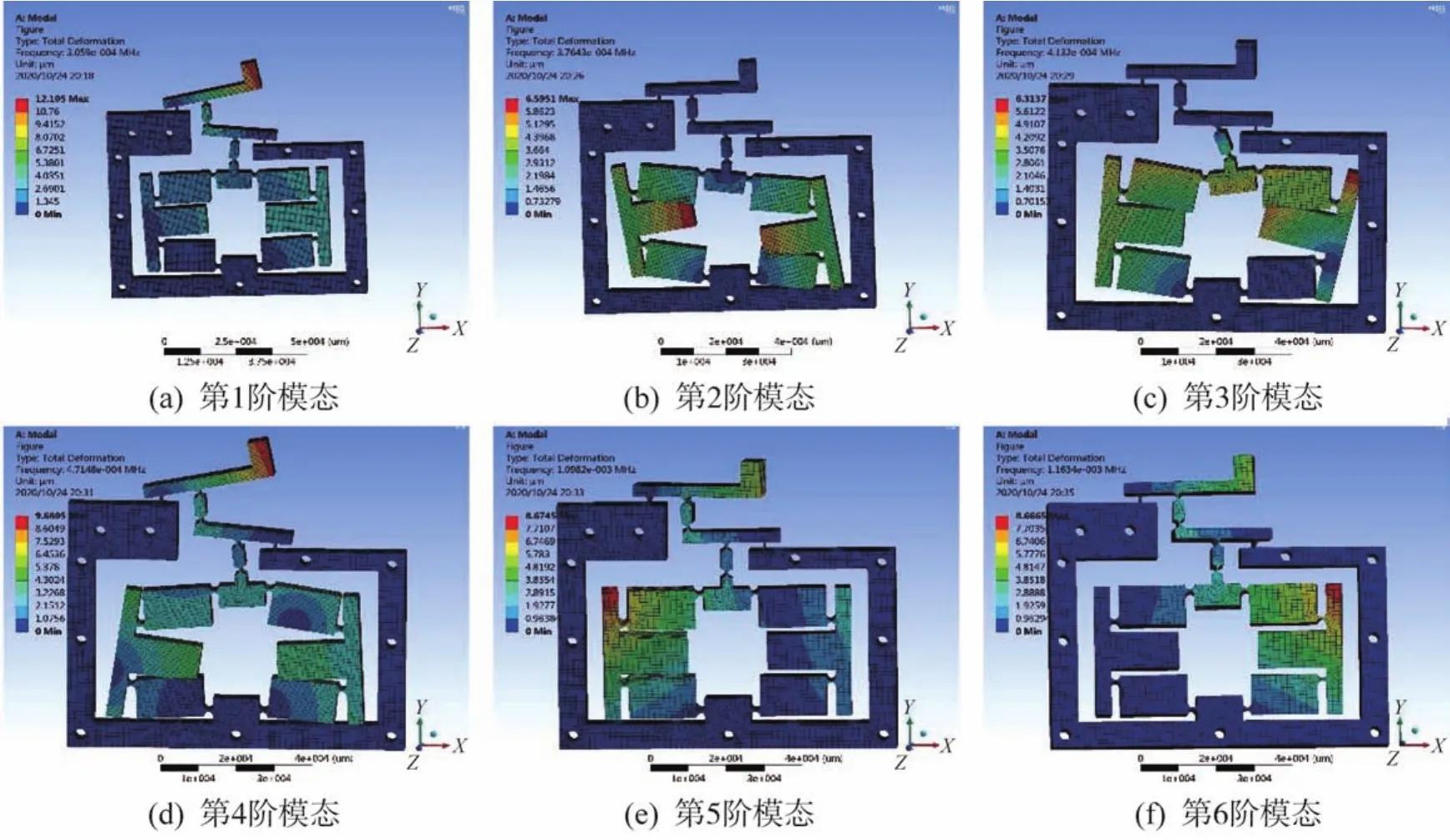
图6 三角混合两级杠杆微位移放大机构前六阶模态Fig.6 The first six modes of triangular hybrid two-stage lever micro displacement amplification mechanism

表3 三角混合两级杠杆微位移放大机构的固有频率Table 3 Natural frequency of triangular hybrid two-stage lever micro displacement amplification mechanism 单位：Hz

由图6可知：机构的第1阶模态与机构的正常运动状态基本对应，基本上没有发生平面的扭曲变形；从第2阶模态开始，三角结构出现了不同程度的扭曲，在第2，3，4阶模态三角结构出现了挤压变形，两级杠杆结构也开始逐渐发生扭曲变形；从第5阶模态开始两级杠杆结构出现明显的向平面单侧的翻转变形，三角结构轻微翻转；相比第5阶模态，在第6阶模态2种结构的翻转幅度有所减小，但仍然存在一定程度的平翻转现象，表明该机构容易在较高阶模态下发生一定程度的偏离平面的振动。

由表3可知，机构的固有频率在第5阶模态发生了骤变，导致机构开始向平面外翻转。

综上可知，第1阶模态的305.90 Hz是仿真条件下最理想的固有频率，此时机构具有较强的抗干扰能力和较好的动力学性能。

3 结 论

1）设计了一种三角混合两级杠杆微位移放大机构。对其两级杠杆结构中的支点铰链类型进行了对比分析，结果表明，直梁形铰链对输入载荷的敏感性较强。并在此基础上，通过理论推导和有限元仿真得到了微位移放大机构的位移放大比分别为30.000和27.132，相对误差仅为9.56%。

2）通过机构静力学和动力学仿真得到机构的相对寄生运动比为0.348 2，第1阶固有频率最佳，表明机构具有较小的寄生位移、较强的抗干扰能力和较好的动力学性能，该结构是有效、可行的。研究结果为压电驱动器或快速反射镜支撑结构实现大量程的位移输出提供了一定的理论指导。