从学生本位出发，深度理解分数概念

钱彦霖

【摘 要】分数是小学阶段学习的一个重要内容，从自然数到分数，这是数概念的一次重大拓展。分数概念的产生，是人类对数认识的一个飞跃。学生对它的理解以及掌握的程度，关系到其数感、模型思想等方面的构建。教师在教学中只有从学生本位出发，才能帮助学生深度理解分数的概念。

【关键词】概念教学 认识分数 一个整体

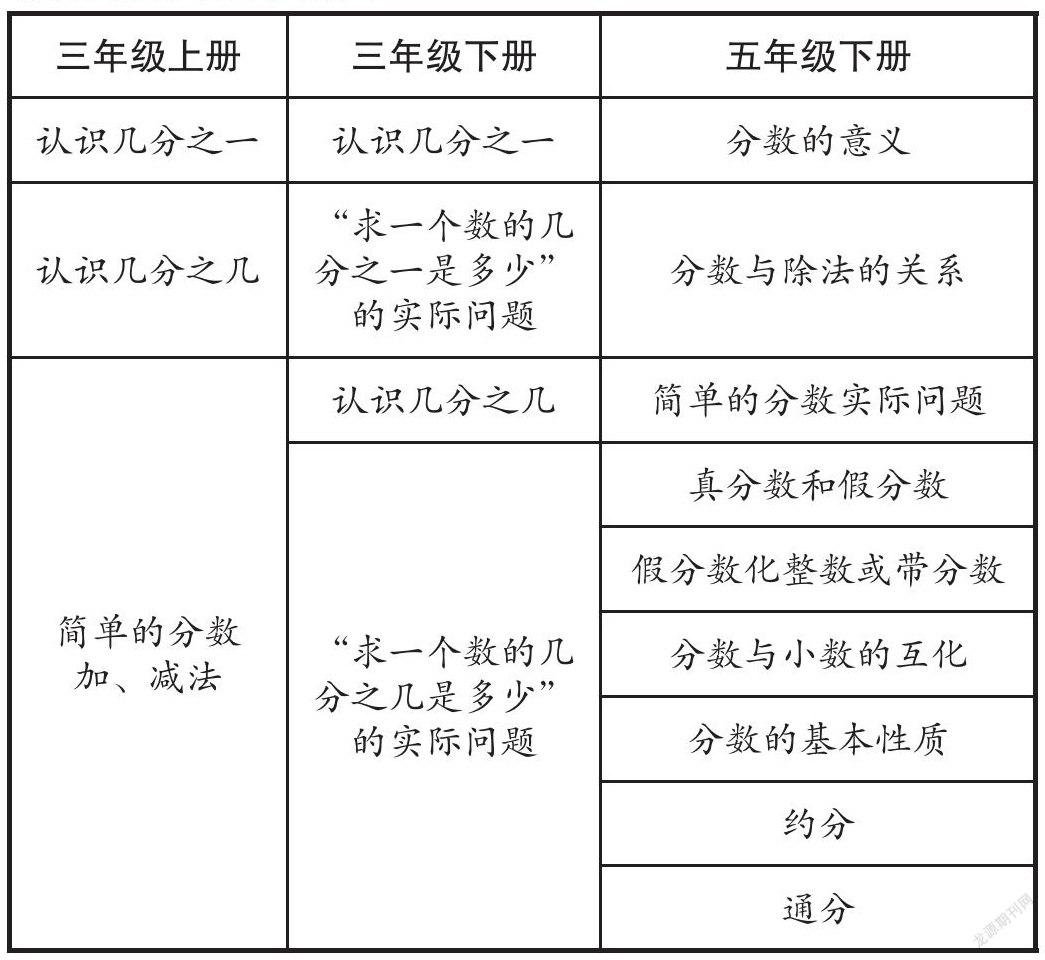
在整个小学阶段，学生学习的数，主要包括“整数、分数、小数”这三类。在一、二年级学生认识整数的基础上，教材在三年级阶段将学生拉向了“分数”这一概念，这是学生对数的第一次拓展，也是其认识上的一次新突破。接着，教材又顺势将学生的思维提高了一个度，让学生认识小数。而就“分数”这一知识点，教材从三个层次进行编排（见下表）：

三年级上册 三年级下册 五年级下册

认识几分之一 认识几分之一 分数的意义

认识几分之几 “求一个数的几分之一是多少”的实际问题 分数与除法的关系

简单的分数加、减法 认识几分之几 简单的分数实际问题

“求一个数的几分之几是多少”的实际问题 真分数和假分数

假分数化整数或带分数

分数与小数的互化

分数的基本性质

约分

通分

分数这一概念是十分抽象的，在教材里出现了三次，而这一知识点也对学生提出了不同层次的要求。在认识一个物体的几分之一时，因为个数只有“1”，所以，大部分同学都能轻易掌握;而当认识一个整体的几分之一时，因为个数由“1”变成了若干个，部分同学无法突破已有认知，所以理解起来开始有难度;学生如果对第二次的分数认识不够，还会影响第三次真正认识分数的含义以及后续的一系列知识。那么，面对分数这一概念，如何从学生本位出发帮助他们真正理解呢？

一、以学生为本，唤醒概念萌芽点

学生第一次接触分数是在三年级上学期，教材（见图1）的设计是从分一分三种物品出发，从具体数量入手，有层次地将4个苹果、2瓶矿泉水和1个蛋糕进行平均分。学生通过思考发现1个蛋糕平均分成两份时，无法用一个整数来表示分得的结果。这时，就产生了引进新数——分数的需要。教师将学生心中的“半个”与分数“”联系在一起，再进一步通过习题练习使学生理解和感悟分数的意义，即把一个物体或一个图形平均分成几份，每份就是它的几分之一。

本节课是学生第二次认识分数（见图2），教材中点明“一盘桃”，其实已经巧妙暗示了“一个整体”，而“平均分给2只小猴”，也需要学生在猴子个数和份数之间建立起联系。但是，中低年级的学生面对有深层含义的分数概念时，往往容易被图中实际数量所影响，无法表示出含有正确含义的分数。所以，在教学这一部分内容时，为了让学生更清楚地体会旧知和新知的区别，更扎实地认识“一个整体的几分之一”，在导入部分，笔者是这样设计的：

师：在动物王国里，猴妈妈给小猴子们采了一个又大又甜的水蜜桃，要是把这个桃子分给2只小猴，你觉得怎么分才比较公平呢？

生：把它们切开，一人一半。

师：对于这种分法，我们把它称为平均分。（电脑演示）

师：如果把一个桃平均分成2份，每份是这个桃的几分之几？

生：每份是这个桃的二分之一。

师：这样的数，我们就叫它分数。它是我们的老朋友，谁能来说一说它是由哪几个部分组成的。

生：分子、分母、分数线。

师：在这个分数中，分母是几？分子又是几呢？你能结合这幅图说一说它们分别表示了什么含义。

生：分母2表示把一个桃平均分成2份，分子1表示其中的1份。

师：互相说一说，把一个桃平均分成2份，每份是这个桃的二分之一。

师：左边这份是这个桃的二分之一，右边这份呢？

生：也是它的二分之一。

师：不一会儿，小猴子们就把这个桃子给吃完了，它们嚷嚷着还不够吃，于是，猴妈妈给它们又准备了一盘桃（PPT出示遮住具体个数的一盘桃），那把一盘桃平均分成2份，每份是这盘桃的几分之几呢？

生：把一盘桃平均分成2份，每份是这盘桃的二分之一。

师：刚才，我们把一个桃和一盘桃都平均分成了2份，最后分得的结果都是二分之一。这两个二分之一的含义一样吗？它们有什么相同点，又有什么不同點呢？

生：不同点在于一个桃和一盘桃，相同点是它们都是平均分成了2份，分得的结果都是二分之一。

师：不管是一个桃还是一盘桃，只要把它们平均分成2份，每份就是它的二分之一。

上述设计基于学生学习经验，遵循知识发展规律，让学生从一个桃过渡到无具体数量的一盘桃，在唤醒分数概念的同时，离“一个整体”更进一步。教师在巩固分数各部分名称和意义的基础上链接新知，为学生接下来的学习奠定基础。

二、以学生为本，展露概念生长枝

分数的本质含义是表示部分和整体的关系。而本节课教学的难点正在于学生容易受到物体总数和每份数量的干扰，难以用整体的眼光正确地用分数表示这种关系。基于学生的真实学情，笔者在教学过程中顺势而为，充分暴露思维冲突点，然后在回忆、比较、辨析中逐步突破难点，建构新知。

师：那猴妈妈到底带来了几个桃子呢？（PPT出示一盘桃子）仔细瞧。

生：6个。

师：把6个桃平均分给2只小猴，每只小猴分得这盘桃的几分之几呢？

（学生分一分）

师：为了看得更清楚，老师用虚线把它们隔开。想一想小猴子得到了这两份当中的几份。

生：1份。

师：我们把每只小猴得到的部分用斜线来表示。上面3个桃子是一份，下面3个桃子也是一份。那这一份是这盘桃的几分之几呢？

生1：二分之一（把一盘桃平均分为2份，每份就是它的二分之一）。

生2：六分之三（因为一个盘里有6个桃子，一份桃子有3个，所以，我认为其中的一份是这盘桃的六分之三）。

师：我们从分数的含义仔细想想分母应该表示什么。

生：份数。

师：所以在这儿，分母要写2。小猴分得其中的几份？

生：1份。

師：分子就写1。我们是把6个桃子看作了一个整体，平均分成了2份，每份就是这盘桃的二分之一。那如果从分数的含义来思考，怎样分才能用六分之三来表示呢？

生：六分之三表示平均分成6份，取其中的3份。

师：二分之一是指把这6个桃平均分成2份，取其中的1份;如果要用六分之三来表示，我们就得把这六个桃平均分成6份，取其中的3份。

师：所以，你们觉得用哪个分数来表示比较合适？

生：二分之一。

如何用份数和总数的关系表示分得的结果，这一直是学生在课堂上容易产生歧义的地方。就例题而言，学生不约而同地给出了两种答案：“六分之三”和“二分之一”。如果只是关注分得的结果，那么一盘桃的二分之一和六分之三其实都表示3个，但如果要联系实际分法以及分得的结果，那么，写二分之一更为合适。教学过程中，笔者始终以“分数的含义”为抓手，引导学生判断哪个更合适，再逆向思考哪种分法用六分之三表示更合适，从而使学生跨越知识的“梗”，突破实际数量与份数之间的矛盾，重新建构新的认知，学生也在这样的过程中实现了思维的生长。

三、以学生为本，完善概念认知田

分数这一概念要在学生的认知田里建构起来有一定难度，但万变不离其宗，教师只要抓住分数的本质特点，就能让学生学会正确表示分数的方法。所以，在设计的时候，教师要充分考虑学生的思维能力，有层次地进行设计，进一步完善分数的含义。

师：正当猴妈妈准备分桃给2只小猴时，又跑来了一只小猴，这下又该怎么分？

生：把6个桃平均分成3份。

师：这时，每只小猴分得这盘桃的几分之几？为什么现在每份变成三分之一了呢？

生：平均分成了3份，其中的一份就是三分之一。

师（追问）：那这一份呢？这一份呢？

生：也是它的三分之一。

师：如果把这盘桃平均分成6份，你能直接分一分吗？

师：现在，我们再来比较一下这三盘桃，同样都是6个桃子，观察一下平均分的份数和分得的结果，你发现了什么？

生：平均分的份数不一样，表示的分数也不一样。

师：看！平均分成2份，最后分得的结果就是它的二分之一;平均分成3份，最后分得的结果是它的三分之一;平均分成6份，最后分得的结果是它的六分之一。你发现了什么呢？

师：把一个整体平均分成几份，每份就是它的几分之一。

在整节课的教学中，教师在思辨中引领学生重新认识“一个整体”的概念，经历多重对比，进一步加深其对分数概念的印象，引领学生自主发现“把一些物体看作一个整体，平均分成几份，每份就是它的几分之一”的结论。整个学习过程可谓层层推进，不断深入，在一个接一个的挑战中、一次又一次的辨析交流中凸显本质，实现了对分数含义的自主建构，完善了学生的概念认知田。

学生是接受知识的载体，教师是传授知识的主导者。有效的概念教学应将概念的逻辑联系与学习者的认知水平有机结合起来，制定或选择恰当、有效的教学策略。所以，在教学过程中，教师要树立以学生为本的教学理念。相信学生一定能掌握复杂深奥的数学概念，也只有在对比中思考、在思辨中成长，学生才能在知识的世界里一步一步走得更为扎实！