树立科学思维方式 提高科学思维能力
——2021年北京高考物理第20题释疑
2022-04-18张晓琳时子豪
张晓琳 时子豪 孟 岩
(北京市第一七一中学,北京 100013)
2021年等级考(高考)物理试卷突出学科主干知识、核心规律、重要方法,注重创新情境的设计,将理论知识与实际生产生活紧密结合,既彰显了物理学科特色,又指引了课堂教学的变革方向.本文以2021年北京高考物理试题中的一道计算题为例,展开案例讨论,谈谈北京新高考中是如何指引了课堂教学的变革方向的.
1 试题再现
(2021年北京等级考(高考)物理试卷第20题)秋千由踏板和绳构成,人在秋千上的摆动过程可以简化为单摆的摆动模型,等效“摆球”的质量为m,人蹲在踏板上时摆长为l1,人站立时摆长为l2.不计空气阻力,重力加速度大小为g.
(1)如果摆长为l1,“摆球”通过最低点时的速度为v,求此时“摆球”受到拉力T的大小;(2)在没有任何人帮助的情况下,人可以通过在低处站起、在高处蹲下的方式使“摆球”越摆越高.
a.人蹲在踏板上从最大摆角θ1开始运动,到最低点时突然站起,此后保持站立姿势摆到另一边的最大摆角为θ2.假定人在最低点站起前后“摆球”摆动的速度大小不变,通过计算证明θ2>θ1.
b.实际上人在最低点快速站起后“摆球”摆动速度的大小会增大.随着摆动越来越高,达到某个最大摆角θ后,如果再次经过最低点时,通过一次站起并保持站立姿势就能实现在竖直平面内做完整的圆周运动,求在最低点“摆球”增加的动能ΔEk应满足的条件.
2 试题探析
2.1 命题意图
科学思维是物理学科核心素养的重要组成部分,培养学生的科学思维能力,是贯穿于整个高中物理教学全过程的重要任务.本题是在熟悉的情境中,注重考查了学生是否具有独立思考、分析问题和解决问题的科学思维能力.引导未来的物理课堂应跳出题海战术,树立学生正确的思维方式、提高科学思维能力、形成科学思维品质,为学生未来的人生奠基.
2.2 试题释疑
2.2.1 如何荡秋千
秋千是中国古代北方少数民族创造的一种运动.新中国成立后,在大部分地区已成为儿童的专项活动.怎样才能越荡越高呢?经验:需要人在最大偏转角处迅速下蹲,在最低点处迅速站立,下蹲和站立的过程都在瞬间完成即可.对本题第(2)问分析如下.
2.2.2 原因探析
解法1:动力学角度.
如果忽略空气阻力,把踏板与人当成一个系统,即:“摆球”质量为m.当系统摆动到某位置时,摆线与竖直方向的夹角φ.
为对其进行受力分析,如图1所示.

图1 踏板与人组成系统的整体受力分析
沿绳子方向

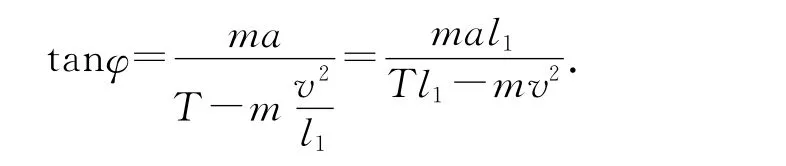
不难发现式中变量太多,很难确定夹角φ的大小.
3.2 肿瘤内局部注射治疗 在X线、B超、CT等影像设备引导下穿刺进入实体瘤后注入无水乙醇、化疗药物和碘剂等,作用于肿瘤细胞,发挥疗效。该方法适合于较小的周围型肺癌或转移性肿瘤在肺野少数孤立性病灶,其单用以及和其他方法联合治疗的疗效尚缺乏大组病例评价[43]。
解法2:摆动过程机械能守恒.
情况1.人在最低点站起前后“摆球”的速度大小不变.
设“摆球”摆动到最低点时的速度为v,情况如图2所示.

图2 踏板与人组成系统“摆球”
由机械能守恒定律可知:最高点A至P的过程

P至最高点B的过程

情况2.人在最低点站起前后“摆球”的速度大小增大.
设“摆球”摆至最低点时速度为v1,人站起瞬间速度为v2,最高点A至P的过程
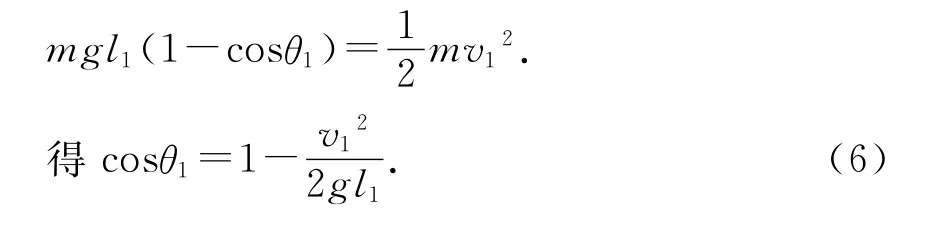
人在最低位置P站起瞬间,所受外力方向过O点,如图3所示.满足角动量守恒:


图3 “摆球”之受力分析

将(7)式代入(8)式中,可得
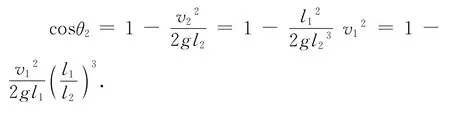

解法3:功能关系角度.
以秋千的踏板为参考系,由于此参考系是非惯性系,故“摆球”摆动到最低点时,还因考虑离心力F,如图4所示.
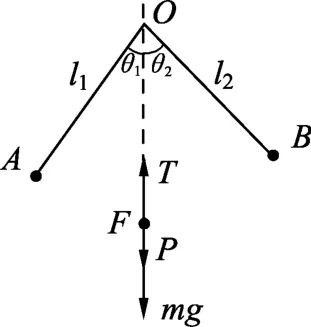
图4 以踏板为参考系,受力分析
人在P位置站起的过程中,人做功为

“摆球”摆动到B位置时,由于ω=0,惯性离心力为零,人在此处下蹲,人只需克服重力做功为
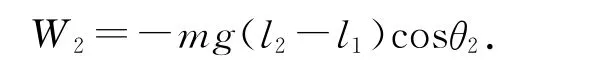
在“摆球”从A经P至B的过程中,人做功为
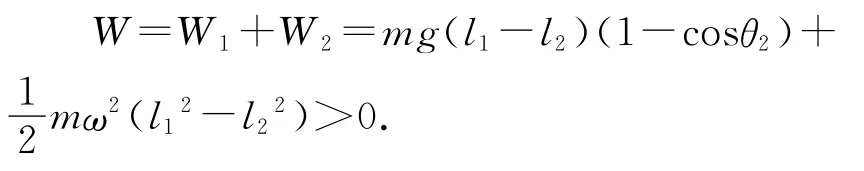
不难发现:“摆球”在摆动中,人在最低点站起、最高点蹲下,人的内力做正功使得“摆球”的机械能增加.这就是人在秋千上得以越荡越高的原因.
2.2.3 运动一周的条件
本题第2-b问是以竖直圆周运动“绳”模型为情景考查力与运动关系.
“摆球”从最高点至最低点P时,满足

在最低点P时人站起,速度增大为v,以O为圆心,l2为半径的圆周运动,如图5所示.通过最高点C时,速度最小应满足

图5 “摆球”运动一周时情景
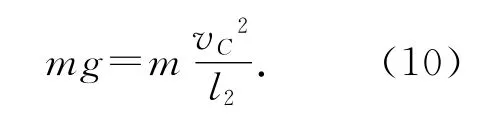
从最低点P至C点的过程中,机械能守恒,有

由(9)~(11)式,可得

即在最低点“摆球”增加的动能满足

3 教学启示
2021年北京高考命题所呈现出来的试题特点,给我们的课堂教学提出了更高的要求:(1)在教学中注重对核心概念、规律的优化与内化;(2)帮助学生建构物理模型,提升其科学思维能力,做到“横向迁移”;(3)跳出题海战术,树立学生科学思维方式,做到“纵向迁移”;(4)经常升级教师自身知识体系,多把生活带进课堂,以适应未来的变革.总之,学会思维是创新时代的要求,为思维而教是教育的目的.
