由平方反比力引入等效势能巧解竞赛题

郑 金

（凌源市职教中心，辽宁 朝阳 122500）

1 利用等效万有引力与等效引力势能

两个或多个质点通过万有引力相互作用，只要推导出其中一个质点受到万有引力的合力的表达式，即可写出等效引力势能的表达式或者等效总能量的表达式.

例1.如图1所示，宇宙中有4个可看成质点的质量为m的恒星，它们稳定地组成了一个边长为L的正方形，求星体做匀速圆周运动的速度.

图1

解法1.由向心力公式和牛顿第二定律列方程［1］

每个星球受到其余三星万有引力的合力大小为

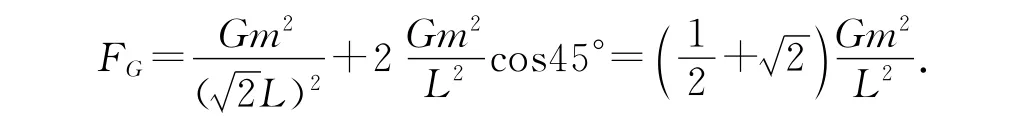
点评：解题关键是推导每个星球受到的万有引力合力大小的表达式，并且指明方向，判断力心不动.

解法2.由机械能公式和机械能守恒定律列方程

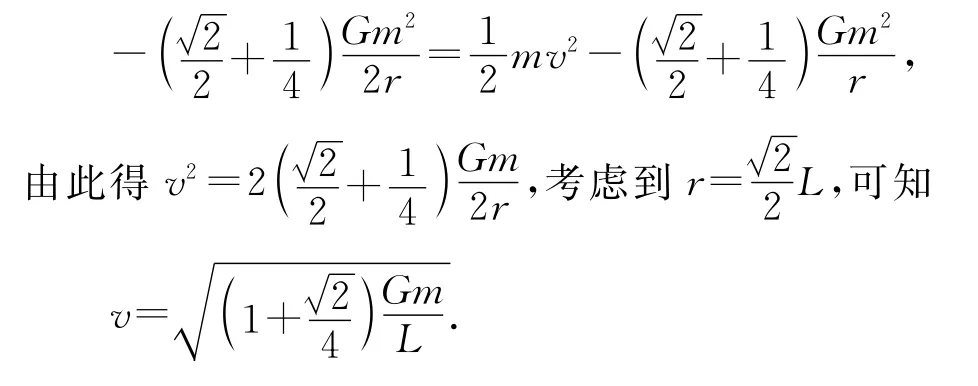
点评：解题关键是推导合力与半径的关系式并设置等效质量M，再利用平方反比力的关系式得出等效势能的关系式以及匀速圆周运动对应的等效机械能的关系式.要注意系统具有的引力势能、每个星球在系统中具有的引力势能以及每个星球在系统中具有的等效引力势能的区别和联系.位于正方形四个顶点的星球系统具有的引力势能等于系统内任意两个星球的引力势能的代数和，即

由此可见，对称系统具有的引力势能等于各星球具有的引力势能之和的一半，每个星球在质心参考系中具有的等效引力势能等于每个星球在系统中具有的引力势能的一半.

2 利用等效库仑力与等效电势能

两个或多个带电质点通过库仑力相互作用，只要推导出其中一个质点受力的表达式，即可写出等效电势能的表达式或者等效总能量的表达式.

例2.如图2所示，两个质点的质量分别为m和M，带相等的正电荷q，相距为l，处在匀强电场内，场强大小为E，方向从质点m指向M.两个质点的初速度均为0，求它们在后续运动过程中距离的最大值.假设质点一直沿直线运动，不计万有引力.

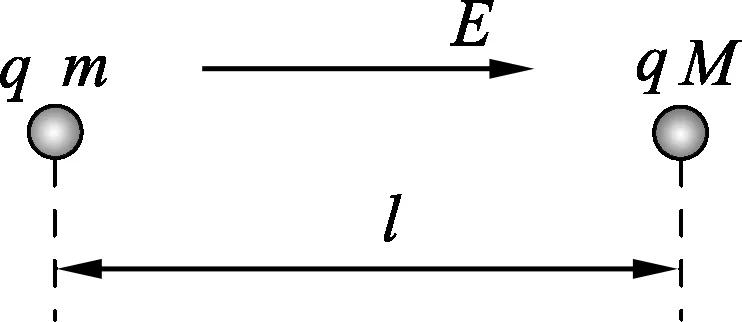
图2

解法1：利用势能曲线以及对勾函数的性质

分析质点m和M的受力情况如图3所示.［2］

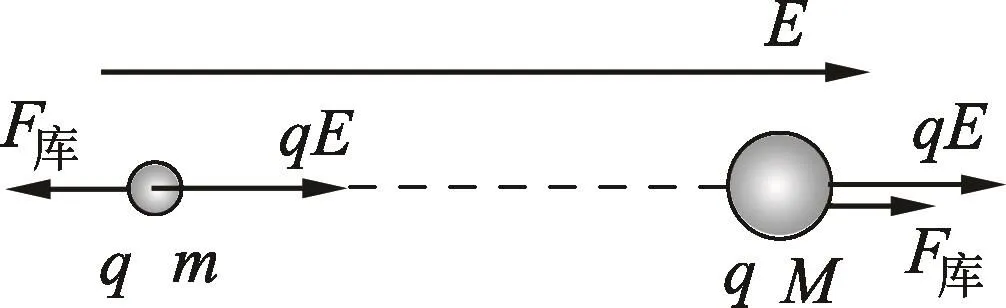
图3

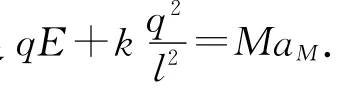
若以质点M为参考系，则质点m受到惯性力的大小为F′=maM，方向水平向左.

在质点M参考系中分析质点m的受力情况如图4所示.以向左为正方向，设距离变量为r，则质点m受到的合力大小为

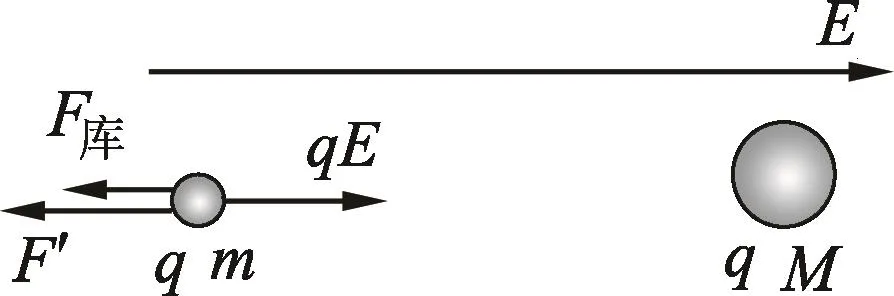
图4

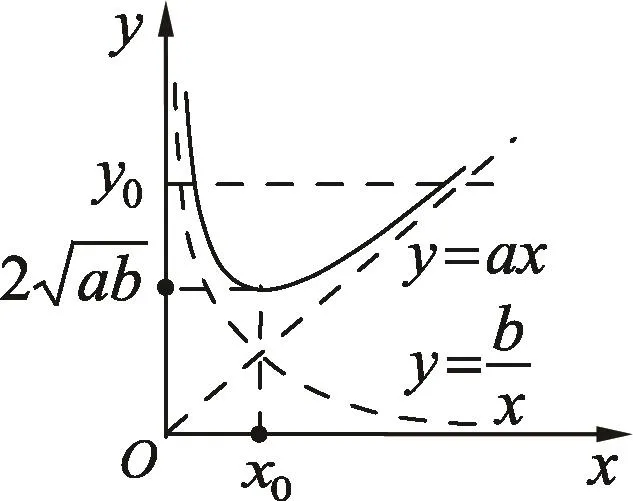
图5

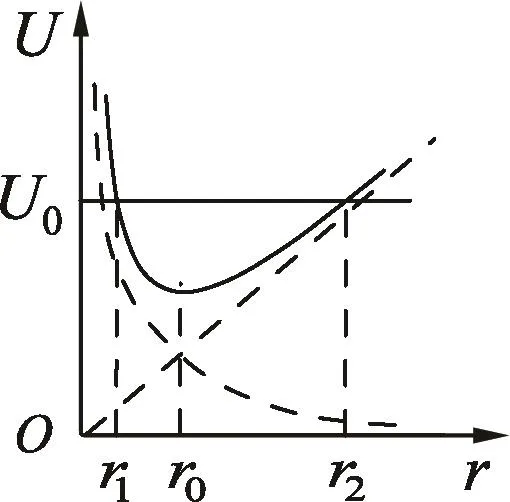
图6

点评：解题关键是推导质点m在非惯性系中的受力关系式，并且写出等效势能的表达式，以利用势能曲线来分析势能的极值条件，从而得到所求结果.值得注意的是，在利用图像法解题时，需灵活应用对勾函数的一些性质，包括图像的形状、函数取最小值的条件以及某一函数值对应的共轭点方程x1·x2=x02.

解法2：利用运动转折点的特点以及求根公式

由于相对直线运动距离存在最大值，则相对运动存在转折点，由于在转折点的相对速度为0，则系统的势能最大，等于开始时的总能量，因此转折点对应的最大距离满足方程U（r）=E=U（l），其中

点评：解题关键是推导系统的等效势能的表达式，以便利用直线运动转折点的特点列方程，由此得到关于距离的一元二次方程，利用求根公式求极值.在解方程的过程中，为了便于书写和运算，需多次设置不同的参量符号；在求极值时，需把判别式的平方根与作用力的绝对值进行联系，以便进行分类讨论.

综上可见，两道物理竞赛题都属于平方反比力的问题，在解答过程中都需推导系统中一个质点受到合力的表达式，以便得出等效势能的表达式以及等效总能量的表达式，即可从能量的角度使问题迎刃而解.值得注意的是，若几个质点构成相互作用的系统是对称的，则系统的质心静止不动，那么各质点绕系统的质心做圆周运动或椭圆运动，只需以质心为参考点；若系统由两个相互作用的自由质点构成，则需选择一个质点为参考系，引入惯性力，在此基础上推导另一个质点受到的合力，由此得出等效势能的表达式.通过引入等效势能，即可应用能量守恒定律列方程，或者利用势能曲线求极值，或者根据直线运动转折点的特点列方程，利用求根公式求极值.