反射光线沿原路返回两平面镜夹角个数分析

王伟民 辛存良

（1.安徽省太和县宫集镇中心学校，安徽 阜阳 236652；2.山东省阳谷县西湖中学，山东 聊城 252311）

从一道几何光学题目说起：

例1.如图1所示，平面镜OM与ON的夹角为θ，一条平行于平面镜ON的光线AB经过两个平面镜的多次反射后，能够沿着原来的光路返回，则两面镜子之间的夹角θ不可能是

图1

（A）30°. （B）20°. （C）10°. （D）1°.

分析：如图2所示，我们作出光线经两个平面镜多次反射的光路图——图2中作出了3次反射的情形，看下可否通过这3次反射相关线条之间的角度关系，来总结从开始到最终每次反射后反射光线与平面镜夹角的变化规律.由于图2中两平面镜的夹角比较大（作图时两个平面镜间的夹角设置很小时，两平面镜之间的区域较为狭窄，作多次反射的光路图不方便），所以，光线在两个平面镜内经过为数不多的几次反射后，最后可视为射线的反射光线可能就不再与平面镜相交了.当然，如果两个平面镜的夹角足够小，开始的入射光线与平面镜的夹角也足够小，那么，当入射光线射向其中的一个平面镜时，理论上我们可以作出任意多次数反射的光路图.

图2

由光的反射定律“反射角等于入射角”可知，每次反射时，反射光线和对应的入射光线与镜面的夹角相等，结合“三角形的一个外角等于和它不相邻的两个内角之和”这一规律（三角形内角和定理的推论）可知，图2中，光线第1次沿平行于平面镜ON的方向射向平面镜上的B点发生反射时，反射光线BC与镜面OM的夹角为θ，接下来，光线BC射向平面镜ON并发生第2次反射时，对应的反射光线CD与平面镜ON的夹角为2θ，再次射向平面镜OM上的D点发生第3次反射时，反射光线DE与平面镜OM的夹角为3θ，……，根据这一变化规律将问题推广至一般情形，便可总结出下面的结论——在对应反射光线与入射点右侧平面镜的夹角不大于直角时，从第一次反射算起，光线发生第n次反射时，反射光线与过对应入射点的平面镜的夹角为nθ.

解析：要使平行于平面镜ON的光线AB经过两个平面镜的多次反射后，能够沿着原来的光路返回，从开始入射考虑，随着反射次数递增，对应反射光线与平面镜夹角逐渐增大的过程中，必须满足某次入射光线是沿着垂直于平面镜方向入射，这次反射对应的反射光线与平面镜的夹角为90°.不妨设这次反射是第n次反射，由上述分析可知nθ=90°，因为n是正整数，所以，两平面镜夹角θ必须为90的因数，而例1给出的4个选项对应的度数，（A）、（C）、（D）选项对应的角度，都能够去整除90°，都满足要求，只有（B）选项对应的度数20°不能整除90°，所以，本题的正确选项是（B）.

对例1而言，入射光线沿平行于一个平面镜的方向射入，经过两个平面镜多次反射后，最终的反射光线是沿原路返回的，不用说这条反射光线是沿着平行于其中一个平面镜的方向射出，我们不禁要问，入射光线平行于平面镜，最终的反射光线也平行于其中一个平面镜的“特殊”光学现象，只有光线沿原路返回这唯一的情形吗？

例2.两个相交平面镜镜面相对，夹角为θ，在两镜面之间垂直于两镜面的平面内，一条光线沿着与某平面镜平行的方向射向另一个平面镜，经过两个平面镜多次反射后，最终恰好沿着与一个平面镜平行的方向射出，若θ的度数为整数，则满足条件的θ的个数为

（A）12. （B）14. （C）16. （D）18.

分析：能够发现，例1给出的物理情形满足例2所给问题的要求——光线沿平行于一个平面镜的方向入射，经过两个平面镜多次反射之后沿原路返回，最终的反射光线一定平行于其中的一个平面镜，但是这一情形并非满足例2所给问题的所有情形.还有一种情形是光线经过两个平面镜多次反射之后，最终的反射光线不沿原路返回但却仍然与其中一个平面镜平行的情况.如图3所示，光线AB沿平行于平面镜ON的方向射向平面镜OM上的B点，由例1所给问题的分析可知，从刚开始入射算起随着反射次数的递增，反射光线与平面镜所夹的锐角也依次递增，图3所示情形中，如果两个平面镜上连续两次反射的入射点到O点的距离恰好相等，不妨设这相邻两次反射的入射点分别为E和F（即图3中OE=OF），则有∠OEF=∠OFE，由于对称，光线EF射向平面镜OM发生反射，之后经两个平面镜多次反射的光路图跟之前光沿A-B-C-D-E路径的光路图关于∠MON的平分线对称，因此，最终的反射光线必然沿平行于平面镜ON的方向射出（图3中未画出与入射光线EF对应的后续多次反射的光路图）.

图3

解析：最终的反射光线沿原路返回时，光线在两个平面镜之间反射次数n与两个平面镜的夹角θ满足等式nθ=90°，所以，θ的度数应该是90的约数，而90的约数有12个，所以，对应的角θ的度数也有12个，分别是1°，2°，3°，5°，6°，9°，10°，15°，18°，30°，45°，90°.

当最终的反射光线不是沿原路返回但又平行于其中的一个平面镜时，对应光路图的前半部分如图3所示，完整光路图如图4所示.图4中，设OE=OF，并设反射角∠OEF=nθ，则∠MFE=nθ，故有180°-nθ=nθ，所以180°=（2n+1）θ，2n+1为奇数，θ度数为整数，而180的奇数约数（除1外）有5个，分别是3，5，9，15和45，所以，对应的θ的度数也为5个，分别是60°，36°，20°，12°，2°，由于2°与光线沿原路返回时得出的角度情形重复了，所以，满足条件的θ的总数应为16个，即本题的正确选项为选项（C）.

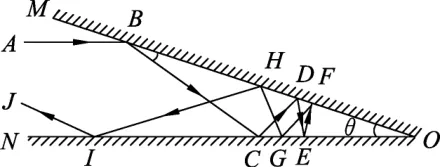
图4

对例2给出的问题而言，如果两个平面镜的夹角度数不受“是整数”这一条件的制约，假如夹角可以是任意度数的话，那么，入射光线沿平行于一个平面镜的方向射入，经过两个平面镜多次反射，最终的反射光线沿平行于其中的一个平面镜射出对应的两个平面镜夹角的度数，不再是有限的几个，而是有无数个.当然，跟例2所给的条件对比，如果两个平面镜夹角度数的限制条件改变，那么，问题的答案也会随之变化.

例3.两个相交平面镜镜面相对，夹角为θ，在两镜面之间垂直于两镜面的平面内，一条光线沿着与某平面镜平行的方向射向另一个平面镜，经过两个平面镜多次反射后，最终的反射光线恰好沿原路返回，若θ的度数为0.02°的整数倍，则满足条件的θ的个数为

（A）12. （B）24. （C）36. （D）48.

分析：能够发现，与例2相比，例3仅仅是将其中的一个限制条件“若θ的度数为整数”更改为“若θ的度数为0.02°的整数倍”，其他条件没有任何的变化，所以，例3的解题思路和方法与例2相同.

解析：当入射光线经过两个平面镜多次反射之后，最终的反射光线沿原路返回时，由以上分析可知，光线在两个平面镜之间总的反射次数n与两个平面镜夹角θ之间的关系式为nθ=90°，因为θ的度数为0.02°的整数倍，所以，可设θ=0.02°k（k为正整数），则有n0.02°k=90°，所以nk=4500，将4500分解质因数得4500=22×32×53，由“因数个数定理”可得，4500的因数的个数等于分解质因数表达式中各质因数指数与1的和的乘积，大小为（2+1）（2+1）（3+1）=36，所以，本题的正确选项为（C）.

两个镜面相对的相交平面镜，在垂直于两个镜面的平面内，光线沿平行于一个镜面的方向射向另一个平面镜，经过两个平面镜的多次反射，如果最终的反射光线是沿原路返回，那么，对两个平面镜夹角度数取值的限制条件不同，满足反射条件的两个平面镜夹角的个数也不尽相同.根据不同的限制条件，利用三角形内角和定理的推论、因数个数定理等数学知识并结合光的反射定律，可以确定满足条件的两个平面镜夹角度数的个数.