基于热方法的骨架提取算法

苏辰耀,刘向阳

(河海大学理学院,江苏 南京 211100)

0 引 言

骨架为形状提供了一种简单且理想化的表示，它的目的是减少形状的维数，同时保持其拓扑形态及其连接特性。基于骨架的目标表示技术在图像压缩[1]、模式识别[2]、形状匹配[3]等领域中有着广泛的应用。

传统的骨架提取方法主要有拓扑细化法[4-6]、距离变换法[7-9]、基于维诺图[10-11]的方法、水平集方法[12-14]等。拓扑细化法从图形的边界向内部不断收缩直至得到骨架，该方法保持了物体的拓扑结构，但是容易受到边界噪声影响。距离变换法[7]通过寻找距离变换脊线来形成骨架，它可以较为精确地找到骨架的位置，但难以保证连通性。基于维诺图的方法[10]是通过维诺图的边和面来提取模型的近似中轴，它能确保骨架的连通性，但是需要剪枝。水平集方法[12]是一种用于界面追踪和形状建模的数值技术，可以有效地处理拓扑结构的变化，通过计算调整最短路径提取骨架。在该类算法中，有效的测地距离计算方法是精确提取骨架的前提。Fast Marching算法[15-16]是计算测地距离的精确算法，其主要思想是通过对程函方程求数值解来近似测地距离。2013年Crane等人[17]提出了热方法，核心思想是由热方程找到距离增加的方向，再还原测地距离。

本文提出一种基于热方法的骨架提取算法，该方法计算了目标形状中每个点到边界的最短距离，通过非均匀扩散的热方法计算得到目标形状的测地距离场，利用梯度下降法获取最终的骨架线。本文算法加入了热扩散系数，将热方法推广到了更一般的非均匀扩散形式。并且在提取骨架线的过程中，引入了投票法检测目标形状的骨架端点，同时提出终点聚类的思想解决了环形骨架的问题。与传统方法相比，本文算法的骨架匹配度更高，可以同时保证骨架线的连续、居中、细化等重要性质。

1 热方法

1.1 主要思想

Varadhan公式建立起了热核和测地距离之间的关系，即：

(1)

其中，x,y是黎曼流形上任意的一对点，t是扩散时间，k和φ(x,y)分别表示热核和测地距离。

热方法在概念上简单而优雅，由于测地距离是程函方程[18]的解，即：

‖φ‖=1

(2)

当t趋于0时，φ近似于每个点到给定源点集的真正的测地距离。热方法只涉及稀疏线性系统，在计算时可以做预处理，并在线性时间内重复使用其中的信息。与传统方法相比，它具有鲁棒性强、精度高、易于操作且成本较低等优点。本文主要讨论热方法在三角网格上的应用。

1.2 空间离散化

为了将连续的过程转变为离散的算法，需要对拉普拉斯算子、梯度算子和散度算子进行空间上的离散化。对于给定的三角网格，点i处的拉普拉斯标准离散化公式为[20]：

(3)

其中，Ai是点i所在三角形面积之和的1/3，j是i的所有邻点，αij和βij是边ij的2个对角。

给定三角面片的梯度为：

(4)

其中，Af是该三角形的面积，N是向外的单位法向量，ei是三角形的第i个边向量(逆时针方向)，ui是其对顶点i的u值。

与顶点i相关的积分散度可以写为：

(5)

其中，包含顶点i的每个三角面片j都有一个对应的向量Xj、e1和e2是三角形j中从i出发的2个边向量，θ1和θ2分别是e1和e2的对角。

2 基于热方法的骨架提取算法

2.1 非均匀热扩散

(a) 原图 (b) 边界距离 (c) 测地距离

(d) 路径集合 (e) 骨架端点 (f) 骨架图1 骨架提取过程

基于热方法的骨架提取算法首先对目标区域进行检测，计算目标形状中每个点到边界的最短距离，将其归一化之后的结果记为De，如图1(b)所示。在图像中给定源点，热量将扩散到同心圆上，测地线是与这些圆正交的直线。为了找到中心化的测地线路径，需要引入热扩散系数。对目标区域构建三角网格之后，公式(6)给出了热方程更一般的形式：

(6)

其中，δ(x0,y0)是以p0=(x0,y0)为中心的Dirac分布，这里p0为目标区域中De最大的点。D是热扩散系数，在均匀的各向同性介质中，D通常表示为一个常数标量乘以单位矩阵，标量代表热传导率。如果各个区域上的热传导率不同，则可表示更一般介质上的非均匀扩散[21]。

为了加快热流在中轴区域的扩散速度，定义D为：

D=eαdf

(7)

其中，α>0为一个常数，本文中α被设为20，df表示每个面片的3个点对应De的均值。

在得到热扩散系数后，非均匀热方程在三角网格上可以离散化为：

(8)

2.2 泊松方程

(9)

通过求解稀疏线性方程组(9),即可得到每个目标像素点到源点的测地距离φ。如图1(c)所示，白色点为边界距离最大的点，即热扩散的源点。

2.3 骨架端点

根据骨架定义可知，骨架点处的距离变换值比其邻域内非骨架点更大。如果一个骨架点在骨架线上只存在一个邻点，则该点被称为骨架端点。为了检测骨架端点，本文引入投票法[22]的思想。在目标形状的测地距离场φ中，将边界上每一个点作为终点，通过梯度下降法依次进行回溯。如图1(d)所示，将有一系列路径l被提取，白色点为源点，灰色点为边界点，黑线表示边界点到源点的路径集合。位于这些路径上的点可以用来定义测地密度：

(10)

其中，N是路径总数，当且仅当点p被路径l经过时，δp(l)=1。设置阈值为ε=max(μ)/M，对于不同的形状，M的值不是固定的，本文中M设为100。在最终结果中，只保留所有路径中测地密度超过阈值的点作为预备骨架点。如图1(e)所示，可以看出，此时灰色的预备骨架点集合已经初步具备了骨架的形态。遍历所有的预备骨架点，将其中关于测地距离φ的局部极大点作为骨架端点，如图1(e)中的黑点所示。以骨架端点为终点，依次进行回溯，即可得到目标区域的连续骨架线，如图1(f)所示。

2.4 环形处理

如图2(a)所示，当目标形状含有环形时，上述的算法无法还原出全部的骨架。显然，在环形中检测到的局部极大值点并不是真正的骨架端点。这里，将其定义为“伪端点”。由于环形本身的几何性质，以环形边界点集关于φ的局部极大值点p为分界，两侧的边界点向相反的方向进行路径回溯，导致环形被分成了2个独立的区域生成骨架。

为了检测伪端点，给每个骨架端点一个编号k(k=1,2,…,K)，K为骨架端点总数。遍历所有边界点，若它对应的路径经过端点k，则将其标记为k。显然，被标记过的边界点会形成K个聚类，如图2(c)所示，每个骨架端点对应的聚类都被标注了不同的灰度。当检测到相邻的类时，将其对应的2个骨架端点标记为伪端点。以其中一个点为源点，重新计算测地距离，将另一个点作为终点回溯的路径加入最后的骨架，即可形成完整的环形骨架,如图2(d)所示。由于热方法在预计算中的大量信息可以被重复使用，所以在计算不同源点的测地距离时，可以减少内存占用和时间消耗。

(a) 伪端点 (b) 初步骨架

(c) 终点聚类 (d) 最终骨架图2 环形骨架提取

算法的整体流程如图3所示。

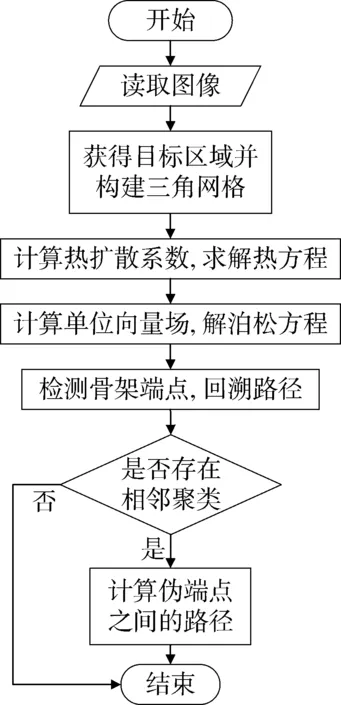
图3 基于热方法的骨架提取算法流程

3 实验结果与分析

3.1 参数评估

图4的目标形状是一个菱形，形状中的黑线是它的骨架。

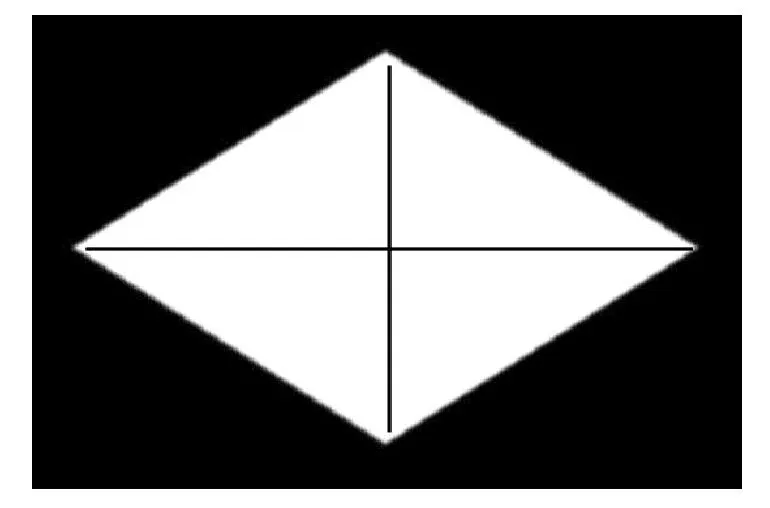
图4 菱形及其骨架线

图5分别设置热扩散系数D中参数的α为0、5、10、20，以菱形中心的白色点为源点得到测地距离。当α=0时，测地距离向周围均匀增大。随着α的变大，中轴区域的测地距离不断减小，从而使得以边界为终点的测地线在回溯时不断向骨架线收敛。

(a) α=0 (b) α=5

(c) α=10 (d) α=20图5 不同扩散速度下的测地距离示意图

3.2 实验结果及分析

本文引入集合论[23]方法，采用骨架匹配度σ评价不同算法得到的结果：

(11)

其中，A表示ground truth中的骨架点集合，B表示本文算法提取的骨架点集合。σ可以综合反映出骨架的连续、居中和细化等性质。

图6是本文算法与传统的Hilditch算法和距离变换法在不同形状的物体上提取的骨架，包括人物、动物等。实验结果见表1。

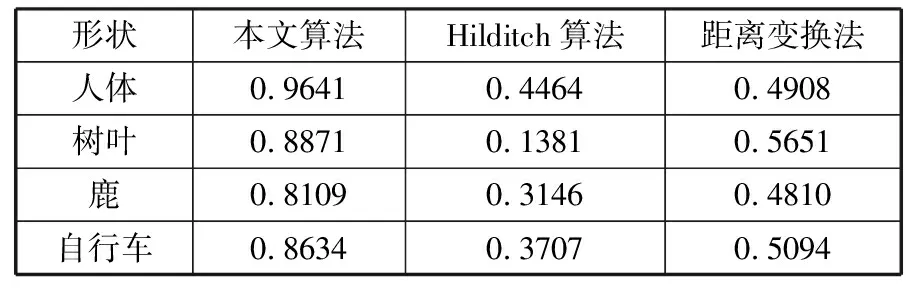
表1 骨架匹配度比较

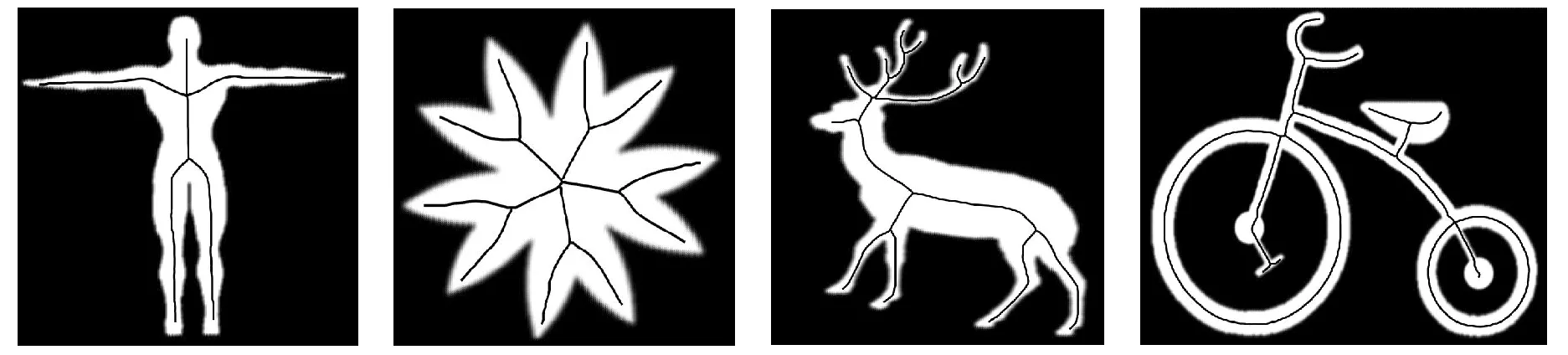
(a) 本文算法得到的骨架线

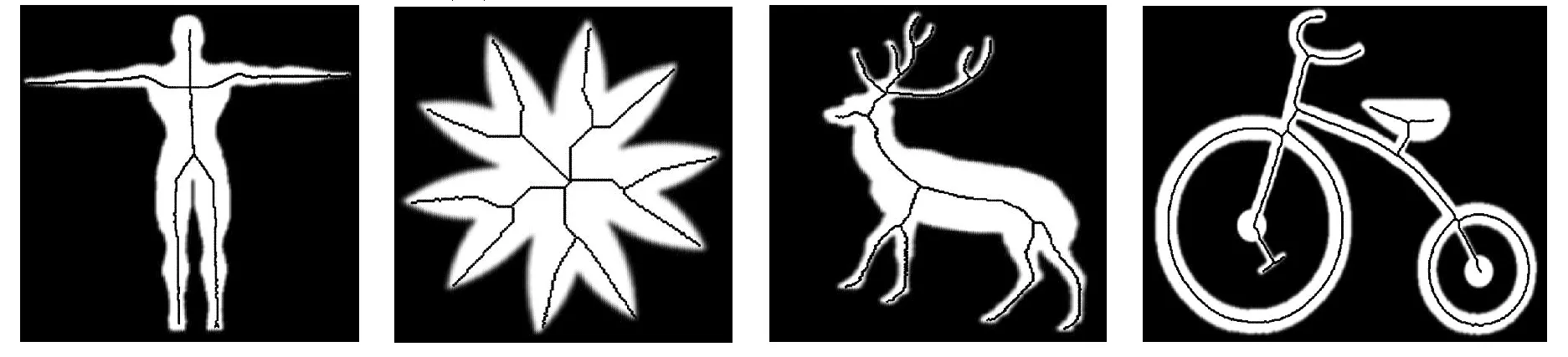
(b) Hilditch算法得到的骨架线

(c) 距离变换法得到的骨架线图6 不同形状的骨架提取

从图6可以看到，本文算法得到的骨架更好地还原了目标形状的拓扑结构，值得一提的是，即便目标形状中含有环形和细小的边，本文算法也可以较好地将其检测并表示出来。与Hilditch算法相比，本文算法得到的骨架位置更为精确；与距离变换法相比，本文算法能够保证骨架线的连通性,骨架匹配度也更高，虽然距离变换法得到骨架的位置更加精确，但是没有对最终的结果进行细化，导致了骨架匹配度的下降。

3.3 二维无序点云的提取结果

点云是物体和形状最一般的表达形式，是无序且不规则的数据。实验结果表明，本文算法的稳定性较好，对于一般的二维无序点云，也可以准确提取出其中的骨架，如图7所示。

图7 二维无序点云的骨架提取

4 结束语

本文提出了一种基于热方法的骨架提取算法。算法中引入了热扩散系数，将热方法推广到了更一般的形式。热方法计算测地距离只需要求解2个稀疏线性方程组，因而成本较低且易于操作。预计算中的拉普拉斯算子、梯度算子和散度算子可以重复使用，在计算环形的骨架时降低了时间成本和内存消耗。实验结果表明，本文算法可以精确有效地应用于目标形状的骨架提取，算法的抗噪能力和稳定性也比较好，具有较好的推广前景。后续工作中，需要进一步研究测地密度阈值的设置并提高算法效率。