基于ABAQUS的卷管式铺管法管道变形敏感性分析

余 杨，刘泽生，余建星，韩梦雪，胡少谦，许伟澎，张春迎，颜铠阳，徐盛博

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.天津大学 天津市港口与海洋工程重点实验室，天津 300072)

海底管道是海洋油气开发的重要工具，承担着油气集运的责任。随着海洋油气开发向深海挺进，管道的铺设方式也在发生变化，铺管船法逐渐取代拖管法成为海管铺设的主流方式。

铺管船法分为3种铺管方式，即“S”型铺管法、“J”型铺管法以及卷管式铺管法。卷管式铺管法是一种新兴的铺管方法，尤其适用于小管径海管和柔性管道的深水铺设[1]。卷管铺设流程可以划分为4个阶段：焊接、预弯，管道上卷，卷筒运输，管道退卷[2]。管道焊接、预弯和上卷过程可以在港口码头同步进行，铺管船停泊在焊接基地所在的港口，将管道牵引、连接至卷筒，控制卷筒转动，同时施加张力，管道曲率逐渐增大，发生弯曲变形，卷入到卷筒，图1(a)为管道上卷示意；随后，铺管船携带上卷后的卷筒离开港口航行至预定铺管海域，卷筒反向旋转，张紧器施加后张力，管道离开卷筒，依次经过校准器、校直器和张紧器后离开铺管船进入海水中，图1(b)为管道退卷示意。

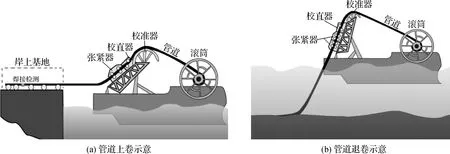
图1 管道上卷、退卷示意

目前，国内外已针对卷管式铺管法展开诸多研究，叶玮[2]针对卷管铺设过程中管道的受力模型进行了解析计算和有限元分析。王立权等[3]分析了铺管过程中管道可能发生的失效形式，并对管道的极限载荷进行了理论分析。张九菊等[4]利用有限元软件ABAQUS对管道椭圆度的敏感参数进行分析,得到了椭圆度随管道几何参数变化的规律。唐彪等[5]利用有限元软件ABAQUS建立了三维上卷校直模型，得到了校直对管道截面的影响规律。邓磊[6]针对管道的不同拉力和弯矩组合进行了理论分析和有限元计算，得到管道的曲率变化规律。王彦辉等[7]着重考虑管道在退卷、校准和铺设过程中的动力学特性，研究管道外径、径厚比和钢材等级对椭圆度的影响。廖洪千[8]基于Ansys对管道校直过程进行分析，分析管道几何、材料参数以及弹性回弹对管道屈曲的影响,并进行试验验证。Yuan等[9-10]针对内衬耐腐蚀衬管的管道上卷展开研究，发现衬管起皱、塌陷曲率随管径、内压变化的规律，并加以证明。Castello等[11]对夹层管的卷管铺设展开分析，发现夹层管的极限强度取决于各层管道界面的剪切应力。Liu等[12]针对Lüders应变、卷筒与管道直径比、管道径厚比等变量展开研究，得到了局部变形模式的幅度和空间分布。Martinez等[13]进行了全尺寸管道的上卷和校直试验，并与数值模拟对比，研究了循环往复的上卷和校直操作对管道椭圆度的影响。

卷管式铺管法的铺管过程十分复杂，目前，王立权等[3]、张九菊等[4]和唐彪等[5]将整个流程简化为管道上卷和退卷过程，针对管道的失效模式、应力变化、曲率变化规律和椭圆度敏感参数进行研究，取得了理想的研究结果。但并未针对管道上卷张力和退卷时的后张力进行敏感性分析，研究其对管道椭圆度、轴向应力、剪切应力残留的影响。

因此文中将研究重点放在管道上卷、退卷两个流程，通过ABAQUS有限元数值模拟对管道设置合理的边界条件和载荷，研究张力和后张力大小对管道椭圆度、轴向应力和剪切应力残留的影响。

1 残余应力理论分析

1.1 上卷时的管道截面应力分布

在上卷过程中，与卷筒发生接触的管道除了受到卷筒外径对其施加的弯矩外，还受到张紧器对管道施加的轴向作用力，在管道与卷筒发生接触的位置选取一段管道，图2为其受力示意。

图2 接触段管道受力示意

卷管在上卷时必然发生塑性变形[14]，可采用如下假设：1)平断面假设，梁的横截面在变形之后仍然保持平面；2)材料的应力—应变关系采用普朗特曲线，并假设拉伸与压缩时弹性模量E相同，屈服极限σs相同[15]，其力学模型如图3所示。

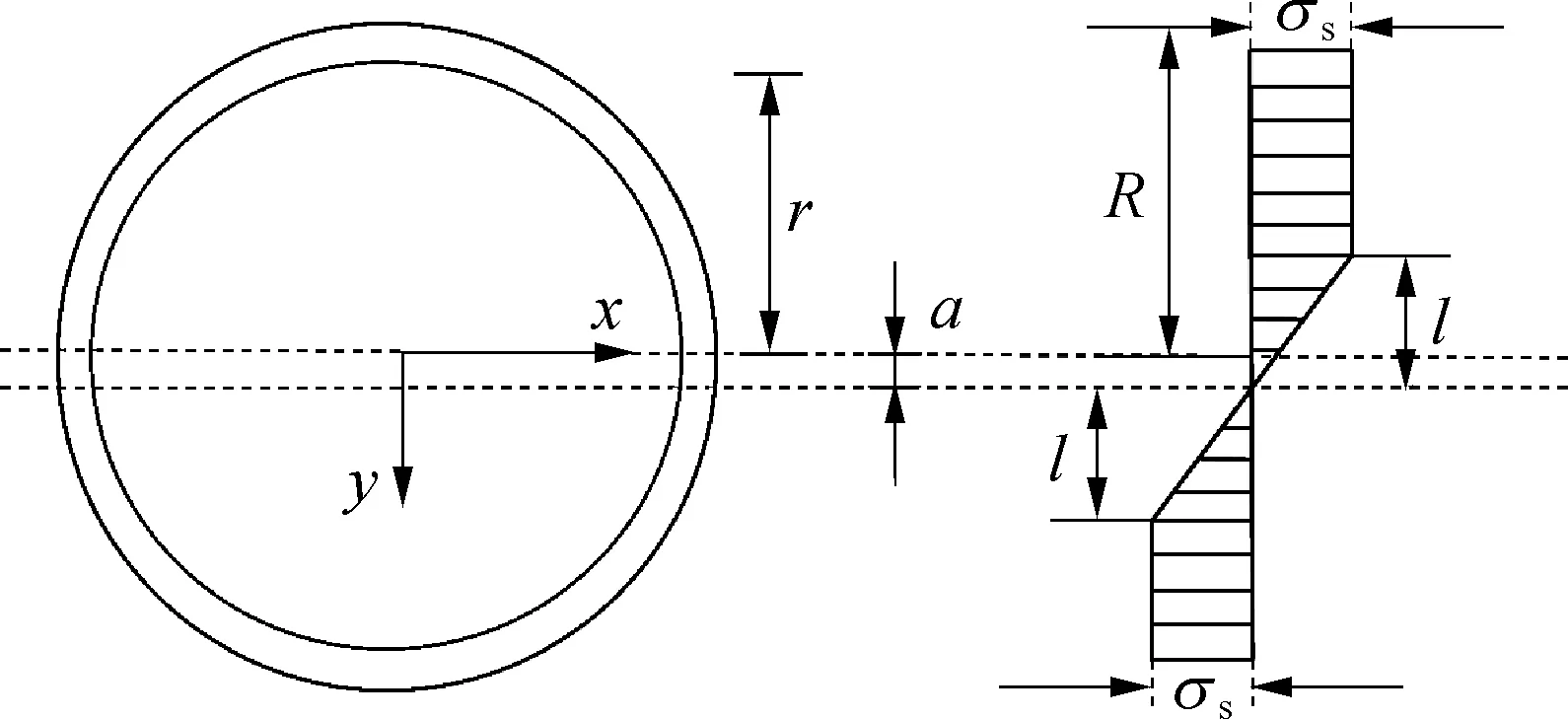
图3 管道截面受力示意

在管道上卷过程中，受到弯矩和轴力共同作用，轴力会导致管道的中性面发生变化，管道上的塑性区域将发生图3所示变化。管道外半径为R，内半径为r，几何中性面向力学中性面偏移的距离为a，管道上开始发生塑性应变的位置到力学中性面的距离为l，管道截面对应的弯矩为：

(1)

(2)

在弯矩作用下，管道会发生弯曲形变，弯曲曲率与卷筒外径直接相关，完成上卷后的管道曲率为一定值：

(3)

式中：D为卷筒直径，R为管道外半径，ρ为中性层曲率半径。

根据胡克定律，海管截面应力可用式(4)表达：

(4)

式中：y为海管截面上所要研究的位置与中性轴的距离。

1.2 退卷时的管道截面应力残留

卸载时，海管截面应力改变量与曲率改变量之间符合弹性关系[16]，即：

(5)

(6)

(7)

式中：Me是弹性极限弯矩，Ke是弹性极限曲率，S是惯性矩。

退卷后，卷筒外径和轴向力对管道施加的弯矩消失，管道上的管道截面残余应力分布是上式叠加，残余应力表达式为:

(8)

式中：ΔM=M是上卷时管道上加载的弯矩，K是上卷时管道的曲率。式(8)中残余应力和张力的函数关系可与后文中的有限元数值模拟结果相互验证。

2 有限元数值模拟模型

2.1 有限元模型材料和几何属性

2.1.1 管道材料本构关系和几何属性

Ramberg-Osgood模型[17]可以准确描述管道材料的非线性属性，有限元模型中管道材料的本构关系表达式为：

(9)

式中：ε是管道轴向应变，A和B是描述管道塑性变形硬化的无量纲参数；σ是材料轴向应力，E为弹性模量，σs是屈服强度，三者单位是Pa。

满足卷管式铺管法弹塑性要求的管道钢材有X60、X65、X70[18]，文中的有限元模型选用X65钢材。

管道模型如图4所示，模型的几何参数与材料属性如表1所示，其中d为管道外径，L为管道长度，δ1为管道壁厚，Δ为径厚比，μ1是泊松比。

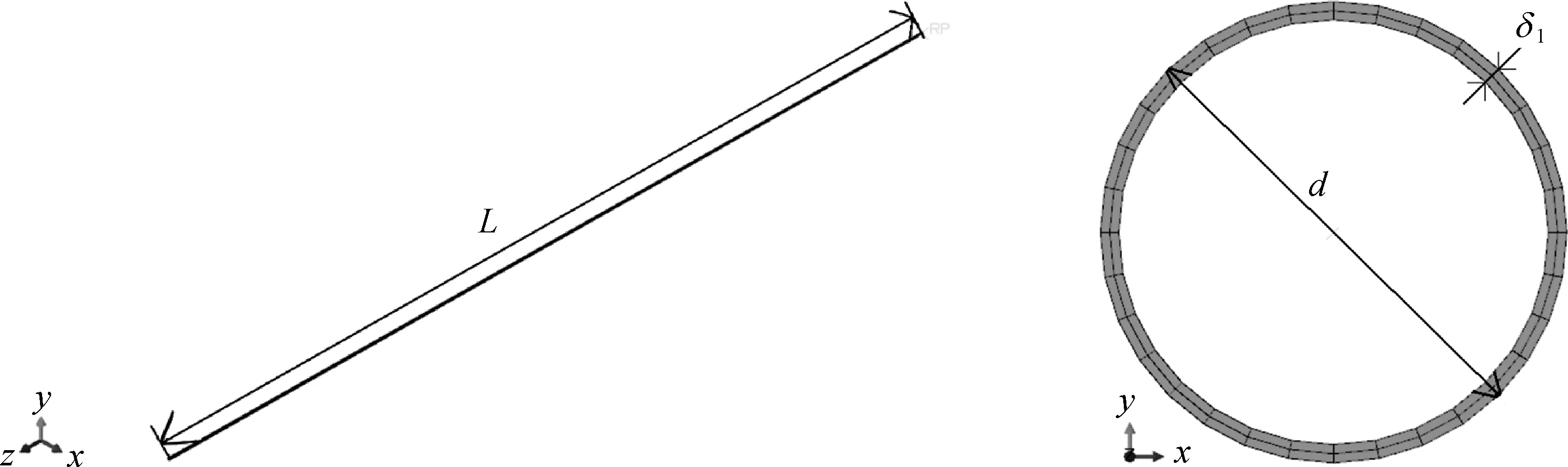
图4 管道模型示意

表1 管道材料属性和几何参数

2.1.2 卷筒材料和几何属性

卷管铺设所使用的卷筒内圈采用钢结构支撑，刚度较大，在铺管过程中不会发生变形[19]，可以将其视为一个刚度极大且不会发生塑性变形的物体，设定其杨氏模量为X65钢材的1 000倍。

卷筒模型如图5所示，卷筒的几何参数和材料属性如表2所示，其中D为卷筒外径，L0为卷筒长度，δ2为卷筒壁厚，μ2是泊松比。

图5 卷筒模型示意

表2 卷筒材料属性和几何参数

2.2 有限元模拟过程

如上文所述，将数值模拟的重点放在管道上卷和退卷两个阶段。数值模拟分为两部分：首先，卷筒逆时针转动，管道末端施加张力，管道缠绕入卷360°；随后，卷筒顺时针转动，管道在后张力的帮助下脱离卷筒。

在有限元模型中，管道会发生较大的弯曲变形，完全积分单元过于刚硬，极易出现剪切闭锁现象，降低计算精度。因此，采用缩减积分单元(C3D8R)进行模拟，C3D8R单元可以有效模拟几何非线性问题[20]。

模型主体分为管道和卷筒两个部分，上卷流程开始之前，需采用tie约束将管道与卷筒固定在一起，此时管道和卷筒的空间位置如图6所示。

图6 管道和卷筒空间位置示意

在管道开始上卷到与卷筒脱离接触的过程中，两者的外表面存在接触，摩擦力无法忽视；模型中，两者之间的摩擦行为选择罚函数进行模拟[21]。

有限元模拟分为两个分析步，第一个分析步中，控制卷筒位移边界条件，使其绕轴心逆时针旋转360°，同时管道右端施加张力F1，管道缠绕上卷如图7(a)所示；第二个分析步中，使卷筒绕轴心顺时针旋转360°，管道右端施加后张力F2，此时，管道脱离卷筒如图7(b)所示。

图7 模型上卷、退卷示意

有限元模型中，针对管道上卷时的张力F1和退卷时的后张力F2进行敏感性分析。根据已有的研究结果，管道张力和后张力的选取与管道材料属性、管径、壁厚等因素有关，在研究过程中，张力F1、后张力F2的选取应该满足式(10)[2，22]：

F≤0.02T0

(10)

式中：T0为管道的屈服张力。

此外，文中所用的管道参数选自铺管船Apache Ⅱ，根据该铺管船张紧器的最大恒张力Tmax=780 kN和已有的铺设经验[23]，选取以下5种工况进行数值模拟，工况1、2、3进行张力F1的敏感性分析，工况2、4、5进行后张力F2的敏感性分析，探究张力F1、后张力F2对管道椭圆度、应力的影响。

表3 工况组合形式

3 管道变形参数分析

为得到管道上卷以及退卷过程中各个时段内的椭圆度、轴向应力和剪切应力，在管道与卷筒相交处右侧13 m处选择截面O进行研究分析，如图8(a)所示。同时，在截面上选择相应的4个(变形情况最明显的特征点[15])研究点如图8(b)所示。

图8 管道研究位置

3.1 张力和后张力对管道椭圆度的影响

根据DNV-OS-F101规范，管道的椭圆度计算公式[24]为：

(11)

式中:f0为管道的椭圆度，Dmax是最大管道外径，Dmin是最小管道外径，如图9所示；D是名义管道外径。

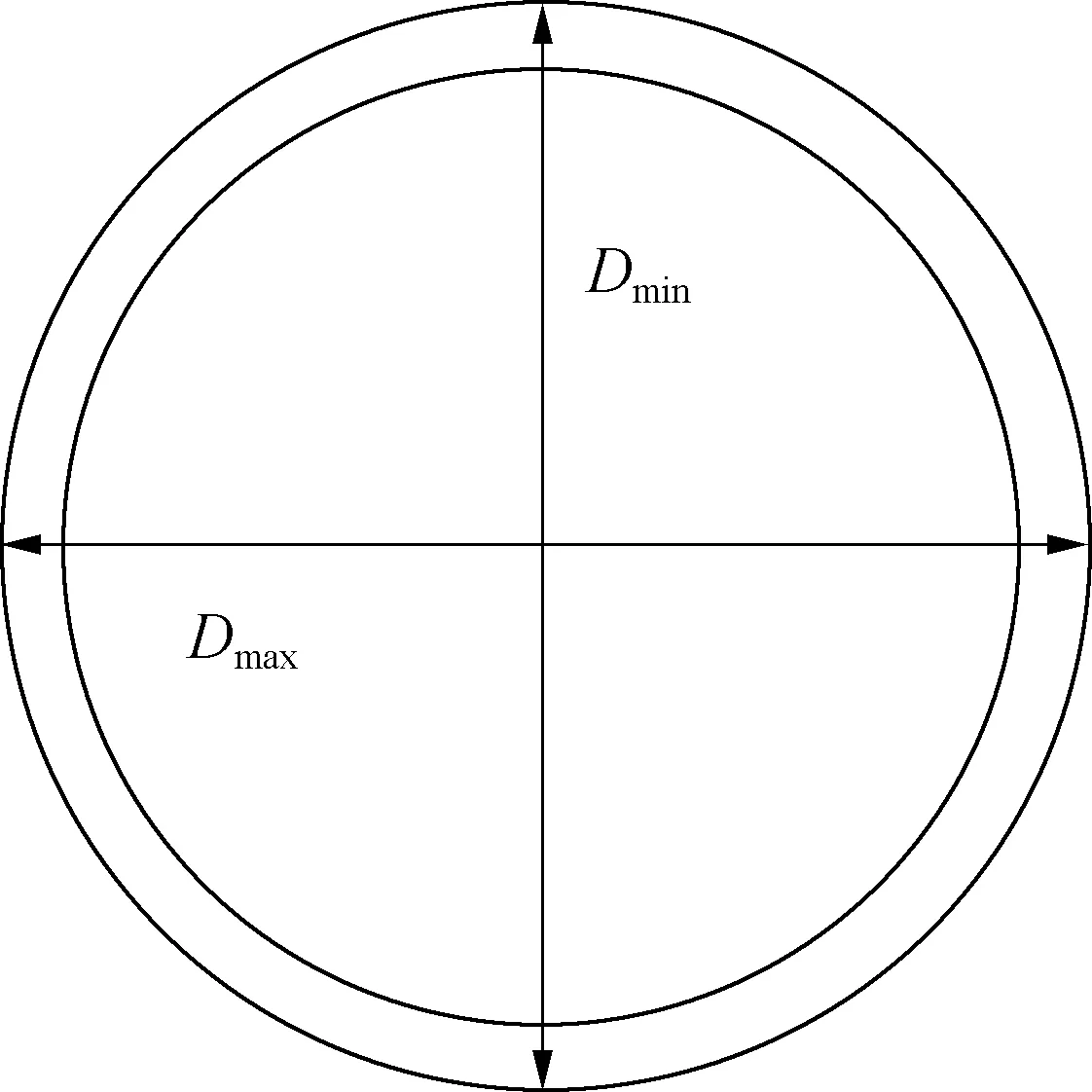
图9 椭圆度计算示意

3.1.1 管道椭圆度变化历程

管道椭圆度在整个上管和退管过程中的变化历程如图10所示。在与卷筒发生接触后，管道椭圆度急剧上升，随后趋于稳定；在即将与卷筒脱离时，管道椭圆度迅速下降，退卷结束后仍保留一定的椭圆度残留。

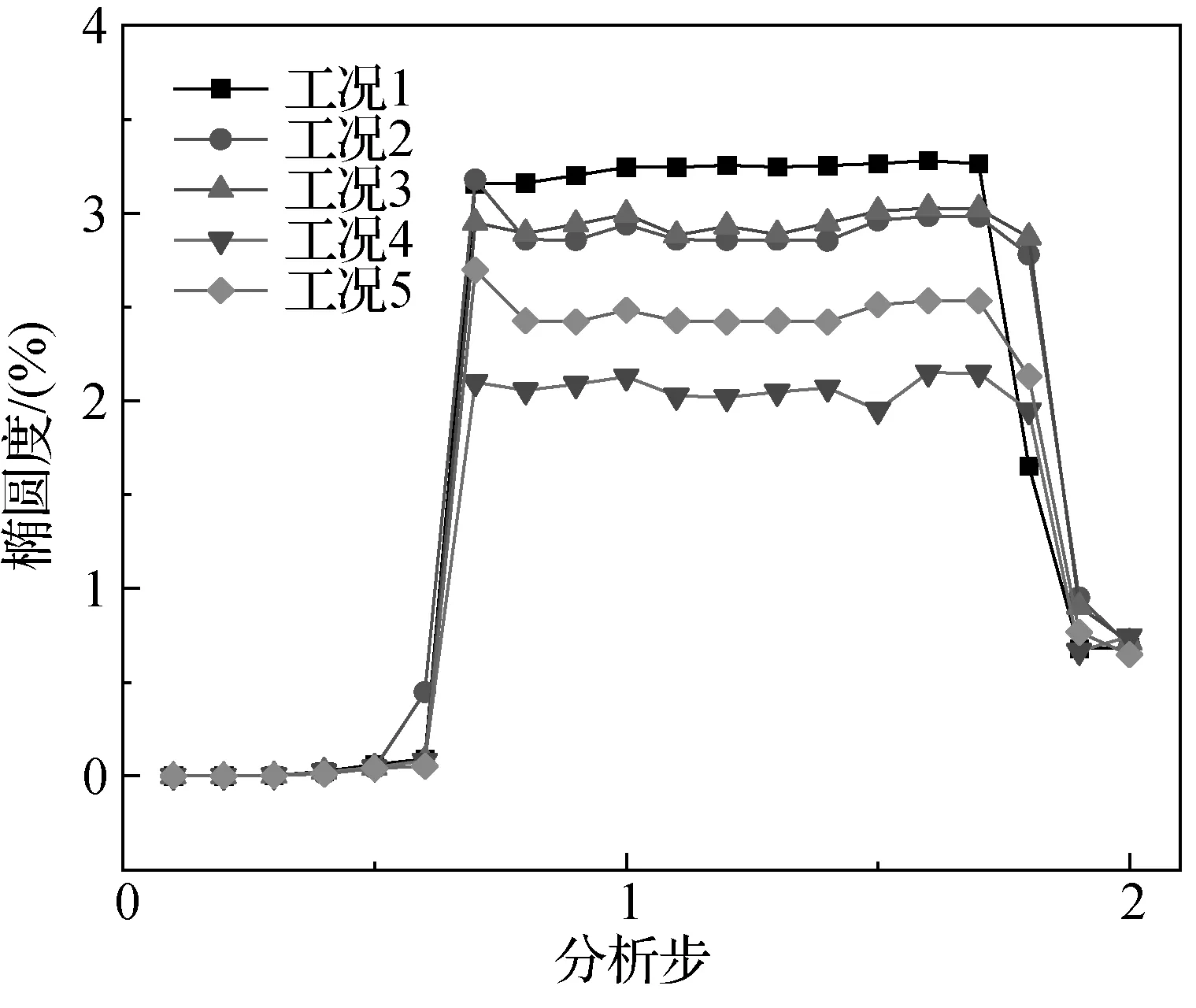
图10 管道椭圆度变化历程

根据DNV-OS-F101规范，当椭圆度f0≥3%[24]时，管道处于失效状态。观察图10中椭圆度的变化历程，可以发现，当管道与卷筒发生接触的瞬间，椭圆度急剧上升，在工况1和工况2中，处于接触位置的管道进入了失效状态；而在工况3、工况4和工况5中管道并未失效。

3.1.2F1与F2对管道残余椭圆度的影响

管道在经历两次大变形后，力学性能和几何形状都发生了一定程度的变化，为衡量管道退卷后的变化状况，现选取管道退卷后的残余椭圆度作为研究变量，绘制残余椭圆度随张力F1和后张力F2变化的曲线如图11所示。

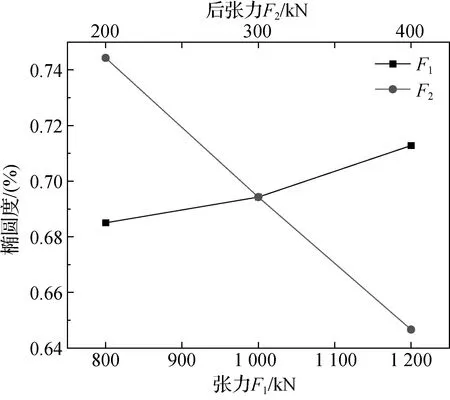
图11 残余椭圆度对比

由图11可以发现，当管道上的轴向张力F1=1 000 kN恒定时，随着管道后张力F2增加，退卷后的残余椭圆度减小；当后张力F2=300 kN恒定时，随着管道张力F1增加，退卷后的残余椭圆度增大。

3.2 张力和后张力对轴向应力的影响

3.2.1 管道轴向应力变化历程

以截面O上各个研究点的轴向应力为例，研究张力F1和后张力F2对轴向应力的具体影响。管道轴向应力在整个上管和退管过程中的变化历程曲线如图12所示。管道与卷筒发生接触，应力迅速上升，随后趋于稳定；管道在即将与卷筒脱离时，轴向应力迅速下降，在退卷结束后会出现反向的轴向应力残留。

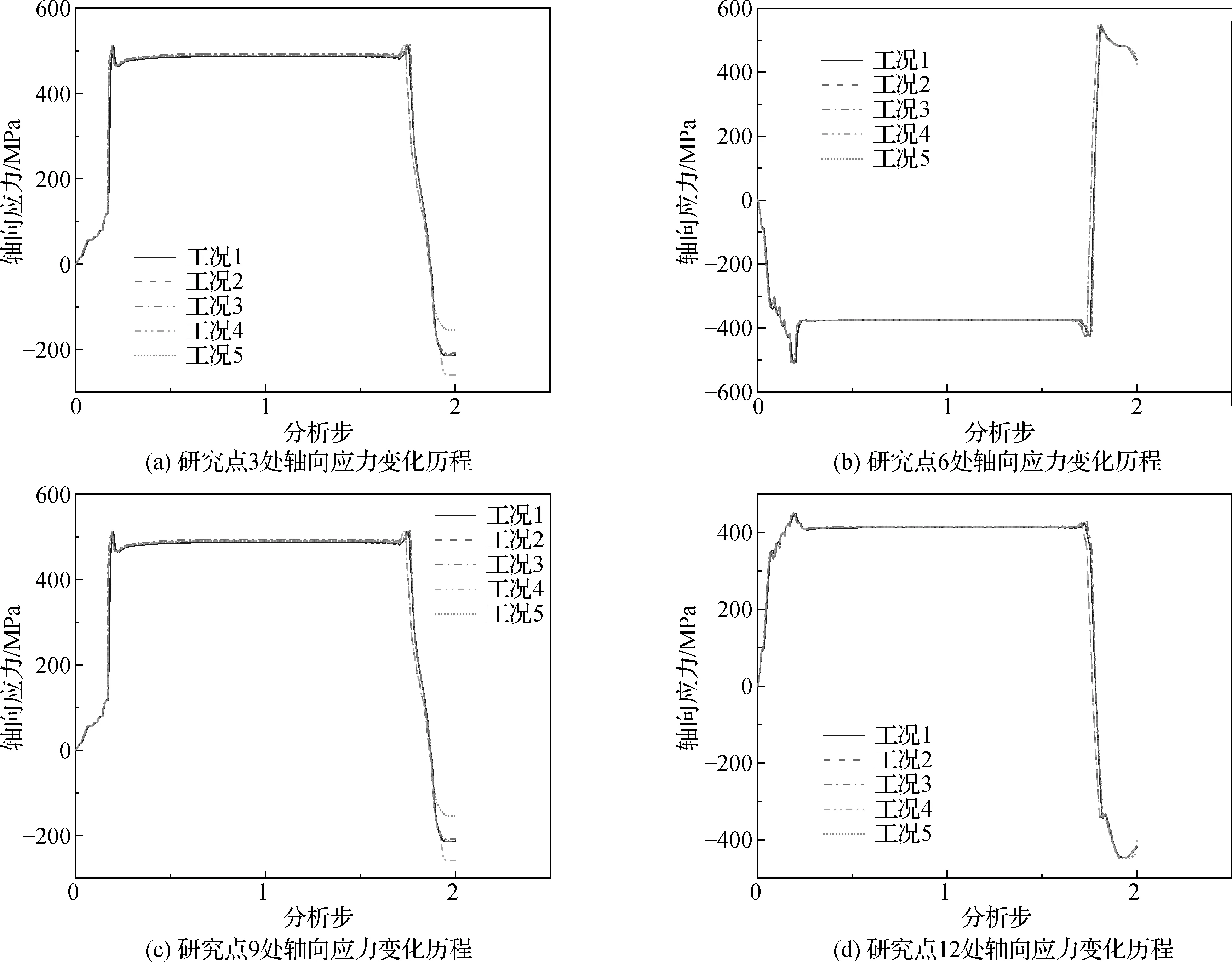
图12 各研究点处轴向应力变化历程

3.2.2F1与F2对管道残余轴向应力的影响

观察图12可以发现，退卷结束后管道上出现了反向的残余轴向应力，为衡量管道退卷后的力学性能变化状况，现选取管道退卷后残余轴向应力的绝对值作为研究变量，各个研究点处残余应力随F1和F2变化的曲线如图13所示。

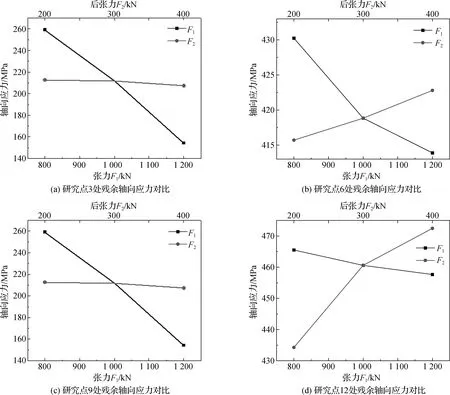
图13 各研究点处残余轴向应力对比

可以发现，研究截面上残留应力最小值出现在研究点9处，约为128 MPa，在此处，残留应力与张力F1和后张力F2呈负相关，并且张力F1对轴向残余应力的影响高于后张力F2；最大值出现在研究点12处，约为472 MPa，在此处，残留应力与张力F1呈负相关，与后张力F2呈正相关。

由式(2)可知，管道上的弯矩M为卷筒外径施加的弯矩和轴向力施加的附加弯矩之和，当卷筒外径恒定时，轴向张力减小会直接导致上卷时管道受到的弯矩减小。在管道截面上取研究点12，此时当y=R时，可以得到残余应力随张力变化的函数图像如图14所示，可知随张力增加，残余应力线性递减，与有限元数值模拟结果有良好的契合性。

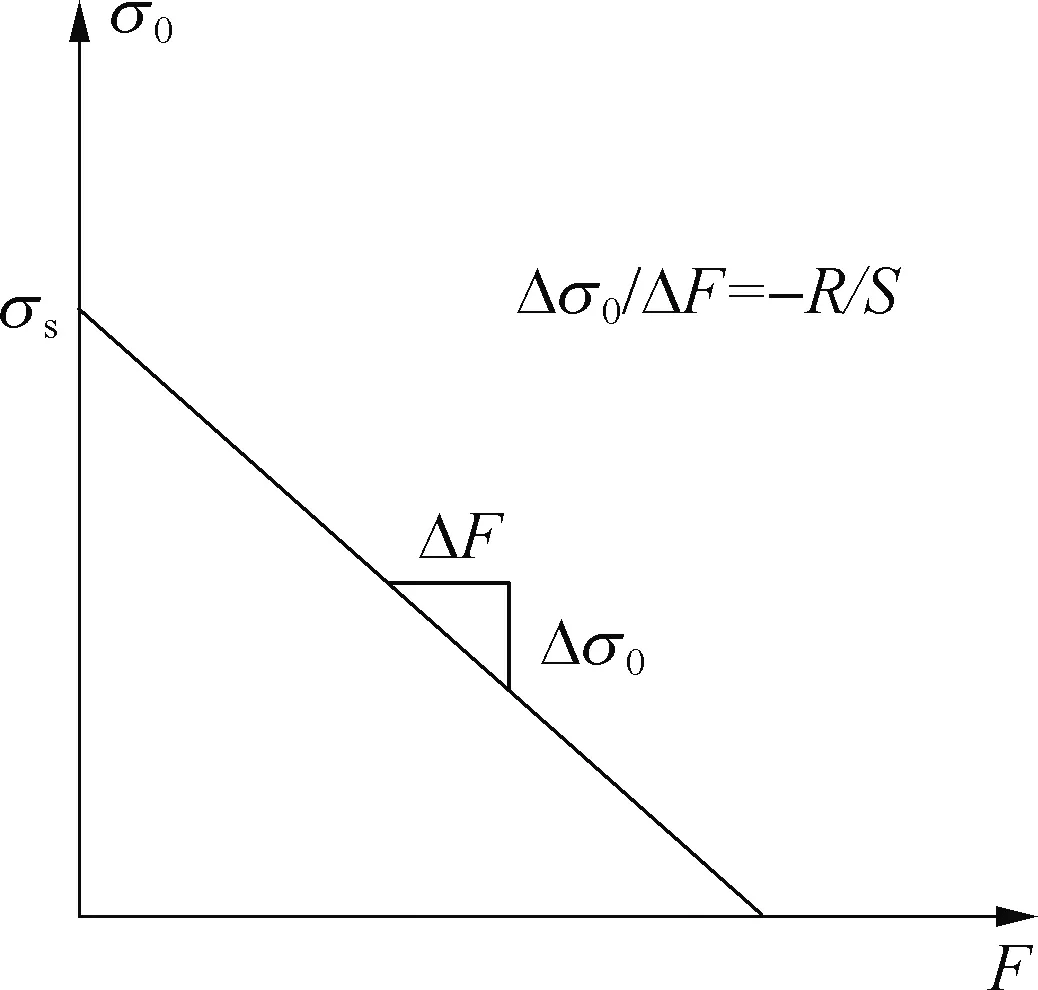
图14 残余轴向函数变化曲线

3.3 张力和后张力对剪切应力的影响

3.3.1 管道剪切应力变化历程

管道剪切应力在整个上管和退管过程中的变化历程如图15所示。管道与卷筒发生接触时，剪切应力迅速上升，管道在卷筒上卷入一段距离后，剪切应力趋于稳定；管道在即将与卷筒脱离时，研究点3和9处剪切应力发生剧烈变化后出现反向剪切应力残留，然而在研究点6和12处，存在正向残留剪切应力。

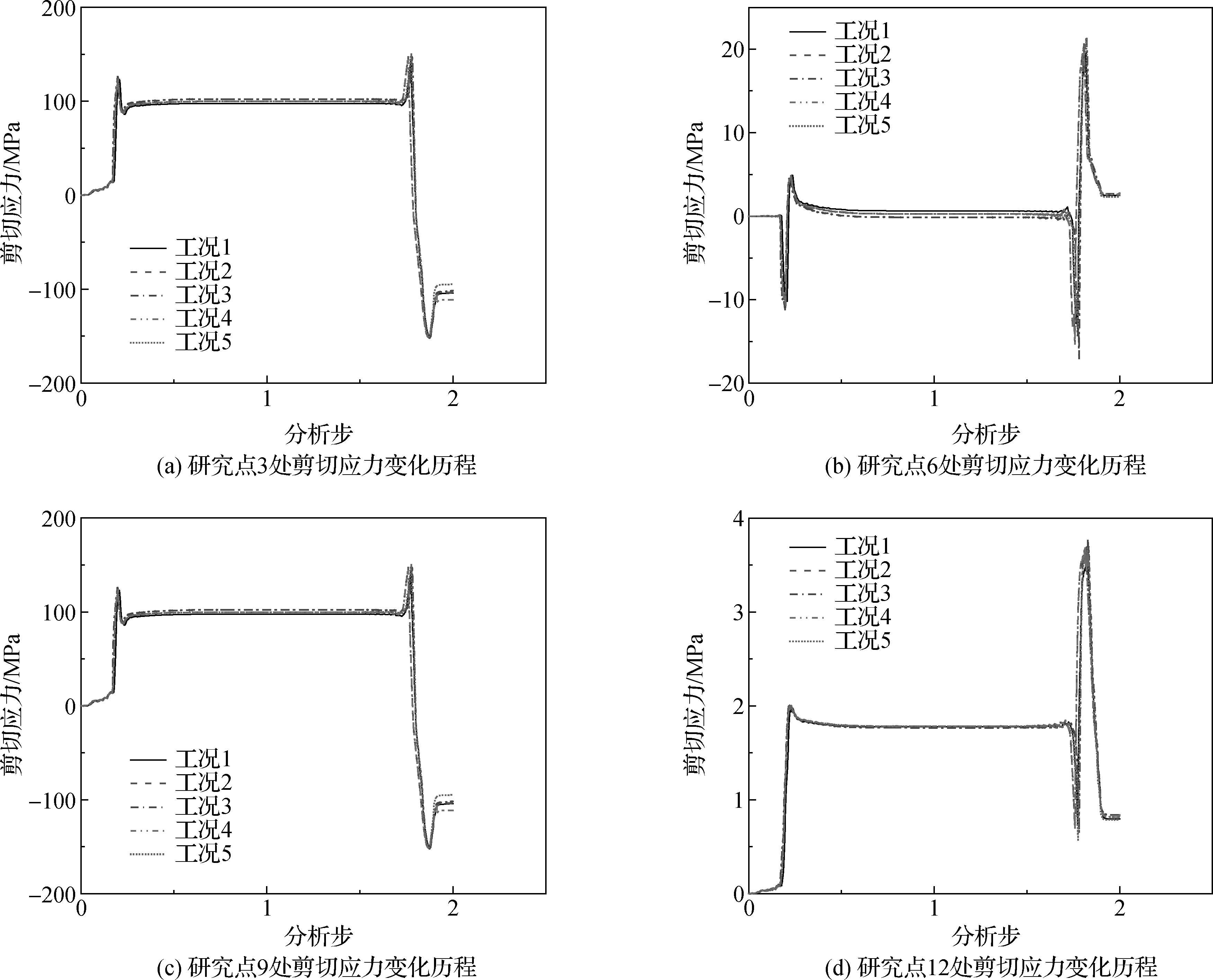
图15 各研究点处剪切应力变化历程

3.3.2F1与F2对管道残余剪切应力的影响

为衡量管道退卷后力学性能变化状况，再次选取管道退卷后的残余剪切应力的绝对值作为研究变量，可以绘制各研究点残余剪切应力随F1和F2变化的曲线，如图16所示。

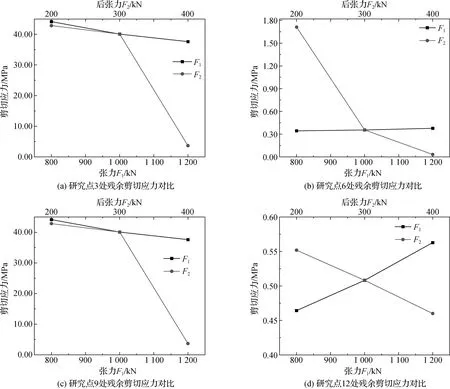
图16 各研究点处残余剪切应力

可以发现，研究截面上残余剪切应力最小值出现在研究点12处，约为0.46 MPa，在此处，残余剪切应力与后张力F2呈负相关，与张力F1呈正相关；最大值出现在研究点3处，约为42.8 MPa，残余剪切应力与轴向张力F1和后张力F2都是负相关，且后张力F2对残余剪切应力的影响高于张力F1。

4 结 语

对建立的有限元模型进行分析，可以得出以下结论：

1)在卷管铺设过程中，管道与卷筒发生接触时，管道上的椭圆度达到最大，此处的管道最容易出现失效现象，增大张力F1，可以有效降低管道在卷管铺设过程中的失效概率。

2)退卷结束后，管道上残余轴向应力的绝对值远大于残余剪切应力，残余轴向应力对管道力学性能变化的影响更加突出。

3)对比管道退卷后残余轴向应力的理论公式与有限元模拟结果，两者具有良好的契合性，可得出相同的结论，随轴向张力F1增大，退卷后的残余轴向应力减小。

4)在退卷结束后，管道上出现了反向的残余轴向应力，张力F1增大，会使管道在退卷结束后的残余椭圆度稍有增大；后张力F2增大，会使残余椭圆度减小，管道在退卷结束后出现的反向残余轴向应力增大。