基于IDDES方法的冲刷地形海底管道绕流数值模拟

2022-04-02曲孟祥梁丙臣

海洋工程 2022年2期

曲孟祥，杨博，梁丙臣, 2，刘欣，张嶔

(1.中国海洋大学工程学院，山东青岛 266100；2.山东省海洋工程重点实验室，山东青岛 266100)

海底管道对于近海油气工业中碳氢化合物的运输十分重要。在可侵蚀泥沙床面上，波浪和水流的作用会导致管道附近的泥沙冲刷，由于受到流动、地形以及土质等各种环境因素的不同影响，冲刷现象十分复杂。随着冲刷坑的发展，当流体绕过管道时，在管道周围会形成复杂且不稳定的分离和尾流结构，并且在管道后方产生旋涡脱落现象，引起管道的涡激振动，最终导致管道疲劳损坏，从而造成环境污染和重大经济损失[1]。因此，研究冲刷过程中圆管周围水动力特征对于石油和近海工业具有重要意义。截止到目前，对于海底管道绕流的研究主要分为两个方面，一是对冲坑地形圆管周围水动力的研究，二是对靠近平坦海床的圆管周围水动力的分析。

对冲坑地形管道周围流场的研究最早可追溯到20世纪70年代，Mao[2]通过试验研究了管道和冲刷床面之间的相互作用，观察了在稳定水流及波动条件下不同雷诺数、Shields参数情况下圆管周围冲刷情况，并得到了冲刷初始阶段5个特征阶段的地形剖面。Jensen等[3]根据Mao[2]的试验结果，对冲刷过程中的5个特征阶段，圆管周围的流场进行了试验研究，分析了圆管周围时均水平流速、时均垂直流速以及涡脱落过程。Smith等[4]分别采用了结合k-ε湍流模型进行封闭的雷诺平均Navier-Stokes(Reynolds average Navier-Stokes,简称RANS)模型及大涡模拟(large eddy simulation，简称LES)模型对这5个特征阶段圆管周围流场进行了数值模拟，通过与Jensen等[3]的试验结果进行比较，验证了两种模型的可行性。计算结果表明，LES模型对于水平流速及垂直流速的预测更为精准，而结合k-ε模型封闭的RANS方法对于涡尺度的计算准确度受网格尺寸影响较大。

对圆管近水平壁面的研究相对较多。Bearman和Zdravkovich[5]通过试验探究了圆管海床之间间隙与圆管直径比值(间隙比)对涡脱落的影响，并分析了圆管周围的平均压力系数，试验表明当该比值等于0.3时，圆管后方出现涡脱落现象，该值也被定义为临界比值。Zdravkovich[6]通过试验测量了靠近平坦海床圆管周围的升力系数及阻力系数，试验表明升力系数主要由间隙比决定，而阻力系数由边界层厚度与圆管海床之间比值决定。Lei等[7]的试验表明了升力系数及阻力系数均由间隙比决定，但受到边界层影响。Wang和Tan[8]在边界层厚度与圆管海床之间比值为0.4的情况下进行了试验，结果表明当间隙比达到0.3时出现了周期性涡脱落。陈蓥等[9]对均匀来流下靠近壁面处在垂直流向做强迫振荡运动的光滑圆柱水动力特性进行了试验研究，通过采集顺流向和垂直流向的力，得到了阻力系数、升力系数、相位角等与间隙比、振荡频率和振幅之间的关系。鄂学全等[10]在试验中利用平板来模拟海床边界，测量了圆间隙比对升力系数及阻力系数的影响，试验结果表明升力系数及阻力系数随着间隙比增大而减小。周磊等[11]通过粒子图像测速(particle image velocimetry,简称PIV)试验研究了间隙比对近壁单圆柱绕流的影响，结果表明随着间隙比的增大，圆柱尾流的流动形态由单个顺时针运动的旋涡演变为逐渐对称的旋涡对，且尺度逐渐减小，同时壁面对圆柱尾流的影响逐渐减弱。在数值模拟方面，Brørs[12]和Zhao等[13]分别应用k-ω和k-ε湍流模型求解雷诺平均方程，模拟了靠近平坦海床的圆管绕流，获得的结果与试验数据相比具有很高的吻合度。谢锦波[14]基于计算流体力学软件FLUENT，结合k-ω湍流模型对横管周围绕流流场进行了模拟计算，计算结果表明所用模型能够较好地模拟速度场、压力场和切应力场分布。Ong等[15-17]在高雷诺数情况下应用k-ε模型进行了数值模拟，研究了涡脱落机理。Zhao和Cheng[18]通过数值模拟研究了湍流场中二维近壁圆柱的涡激振动问题，分析了在间隙比分别为0.002和0.3的低间隙比情况下，边界层对涡激振动的影响。

通过对近壁面圆管绕流问题研究进展的总结可以发现，前人多采用求解RANS方程或者大涡模拟进行计算。考虑到雷诺平均方法在捕捉流场细节方面效果不佳，而大涡模拟又存在对计算资源要求巨大的问题，因此这里采用Spalart-Allmaras改进延迟分离涡模拟(improved detached eddy simulation，简称IDDES)以更深入地分析海底管道周围流场特性，该模型对边界层内的流动采用雷诺平均方法，对边界层外的流动采用大涡模拟，在节省计算资源的同时可以模拟湍流的分离，因此可以更深入地分析圆管周围水动力特征。

1 数学模型

混合模型的诞生主要为了弥补RANS在捕捉流场细节方面的不足，同时避免LES较大的计算量，最初是由Spalart等[19]在1997年提出的一种混合RANS/LES的分离涡(detached eddy simulation，简称DES)模型。该模型是一个使用单一湍流模型的三维非定常数值模拟方法，在网格密度满足大涡模拟要求的区域应用LES模型，在近壁面附近网格密度满足RANS要求的区域应用标准的Spalart-Allmaras湍流模型[20]解雷诺平均Navier-Stokes方程，从而大幅减少计算时间[21]。

在构造RANS/LES混合模型时，需要对方程中的耗散项进行转换，方法是构造一个开关函数。RANS/LES的转换则通过引入长度尺度来判别。DES方法的长度尺度被定义为：

dDES=min(d,ψCDESΔ)

(1)

式中：d为与壁面最近的距离；ψ是低雷诺数修正系数；CDES为经验常数，建议取值为0.65；Δ为网格尺度。

在壁面附近，d≪ψCDESΔ时，采用Spalart-Allmaras湍流模型[19]进行计算；在ψCDESΔ≪d区域时，采用亚网格模型进行计算。

但是当网格密度介于LES模型与RANS模型要求之间时，该模型不能捕捉全部的流场紊动，模拟的涡流黏性与雷诺应力将减小，即模拟应力耗尽现象(modeled stress depletion,简称MSD)[22]。为了解决由网格密度引起的近壁面处模拟应力耗尽的问题，Spalart等[22]在标准DES模型的基础上开发了延迟分离涡(delayed detached eddy simulation，简称DDES)模型。DDES模型通过涡流黏性检测边界层的位置，并强制边界层内的流场由RANS方法求解。

DDES方法长度尺度为：

dDDES=d-fd·max(0,d-ψCDESΔ)

(2)

式中：fd为与涡流黏性相关的函数。在LES区域(rd≪1)，fd等于1，DDES模型即为DES模型；在其余区域fd等于0。

Spalart-Allmaras IDDES模型是由Shur等[23]基于DDES和WMLES(wall modeled LES)改进的RANS/LES混合模型。WMLES模型在边界层内部区域使用雷诺平均方法，在外部使用大涡模拟，但在RANS和LES模型切换区域存在偏差。IDDES模型解决了该问题，该模型将计算域分为三类子域，分别为远离壁面区域、近壁面区域、二者之间区域。当入流条件中没有湍流时，IDDES模型中的DDES方法就会被激活。当入流条件中有湍流且网格密度精细到足够覆盖边界层内的涡时，IDDES模型中的WMLES方法就会被激活。RANS和LES两种方法通过式(3)结合在一起：

dIDDES=fB(1+fe)dRANS+(1-fB)dLES

(3)

式中：dRANS=d，dLES=ψCDESΔ，fB及fe为经验函数。

2 计算模型

2.1 计算域及边界条件设置

利用OpenFOAM模拟了在稳流条件下冲刷初始过程中4个特征阶段管道周围的流动，每一个阶段都有固定的冲刷地形。4个冲刷地形取自Mao[2]通过冲刷试验测得的床型剖面，每个阶段的冲坑深度与管道直径比值G/D分别为0.11、0.42、0.54及0.72。流场计算域总长度选取为40D，计算域高度、宽度分别选取为11D、4D。管道中心放置在(x，y，z)=(0，0.5D，2D)，管道长度为4D，其中D为管道直径，见图1。

图1 模型计算域

圆柱壁面和冲刷床壁面采用无滑移壁面边界条件，流域上下边界采用对称边界条件，流域两侧边界采用周期性边界条件[24]。空间离散采用线性插值格式，时间离散采用向后差分格式。

通过采用雷诺相似准则，设置圆柱直径D为1 m，入流速度为1 m/s，通过修改黏性系数μ使雷诺数与Jensen等[3]试验一致(Re=6 000)。

2.2 网格设置

计算网格采用全结构化六面体网格，并对圆管周围及床面附近的网格进行了加密，如图2所示。表1列出了每个算例的网格数、近管道壁面及近床面区域的网格厚度，4个算例的流场计算域网格节点数均为1.2×107左右，其中近管道壁面及近床面区域，物面法向方向上第一层计算网格最大厚度均为0.002，y+值均在1左右。

图2 模型网格

表1 模型网格

2.3 入流边界层处理

在Jensen等[3]试验中，边界层厚度为2D。为了与试验一致，研究在计算海底管道绕流前，先模拟了稳流在4个无管道的固定床型剖面随时间充分发展的过程，计算了模型的入流边界层厚度及速度入口，以验证边界层设定与试验一致。

首先建立了4个无管道床型剖面的计算域及网格，计算域整体长度为40D，高度为11D，宽度为4D。通过OpenFOAM对4个算例进行模拟，至计算域内流动充分发展后达到稳定。计算结果表明，4个模型得到的边界层厚度与试验条件十分接近，均为2D左右，表明该方法设定入流边界条件较为可靠，因此取4个算例稳定后的入流口速度分别作为后续有管道模型数值模拟的入流口速度。

3 模型验证与结果分析

3.1 模型验证

Jensen等[3]通过试验分析了冲刷床剖面上固定管道周围的流场，试验中通过声学多普勒流速仪测量了几个上游和下游纵向位置的水平和垂直速度剖面。文中研究通过模拟水平管道周围的流速，与该试验结果进行比较，以验证计算模型的可行性及准确性。从模拟结果中提取了与试验相同监测剖面的速度值，并将试验数据无量纲化处理后进行对比：

(4)

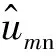
模型对流速的预测结果通过相对均方根误差(RMSD)进行客观评价，均方根误差定义为：

(5)

图3和图4分别为时均水平流速模拟结果及时均垂直流速模拟结果与Jensen试验数据的对比。图3表明，4个算例中，数值模拟对于圆柱上游(-3≤x/D≤-1)来流水平流速的预测与试验结果十分一致，证明了模型定义边界层方法的可靠性;对圆柱尾流区(0≤x/D≤4)的预测出现了偏差，但偏离程度较低；总体来说，在水平流速的预测上模拟结果较为精准，且可以明显看出在圆柱后方8D存在扩展边界层。从图4可以看出，数值模拟对于垂直流速的预测效果欠佳，4个算例中，对于圆柱上游处(-3≤x/D≤-1)时均垂直速度预测略高于试验结果，尤其在地形开始变化的区域(x/D=-1)预测偏差逐渐增大，对于圆柱尾流区域(0≤x/D≤4)的计算误差十分明显。通过分析，数值模拟对于时均水平流速预测效果很好，但对于时均垂直流速的预测偏差偏大，尤其是在冲刷坑以及沙坡附近的边界层区域，极有可能是由于冲刷坑深度增加以及沙坡推移，造成边界层的复杂变化，而IDDES模型在边界层内区域采用雷诺平均方法求解，再加上复杂边界的影响使得计算精度降低，过分高估了沙坡的影响，致使对垂直流速的计算高于试验结果，但整体上流速变化趋势曲线与试验曲线接近一致。

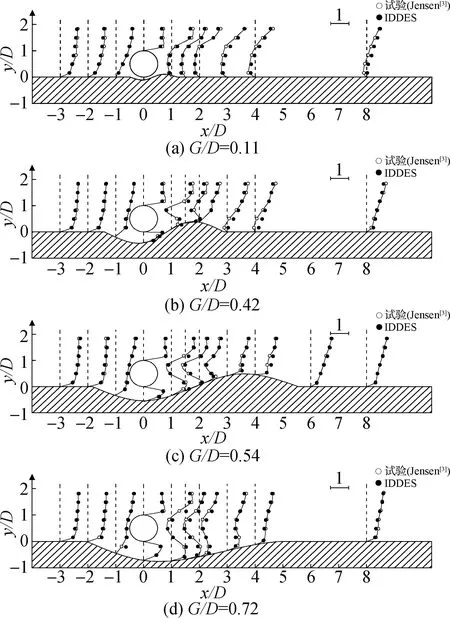
图3 时均水平流速对比(z/D=2)

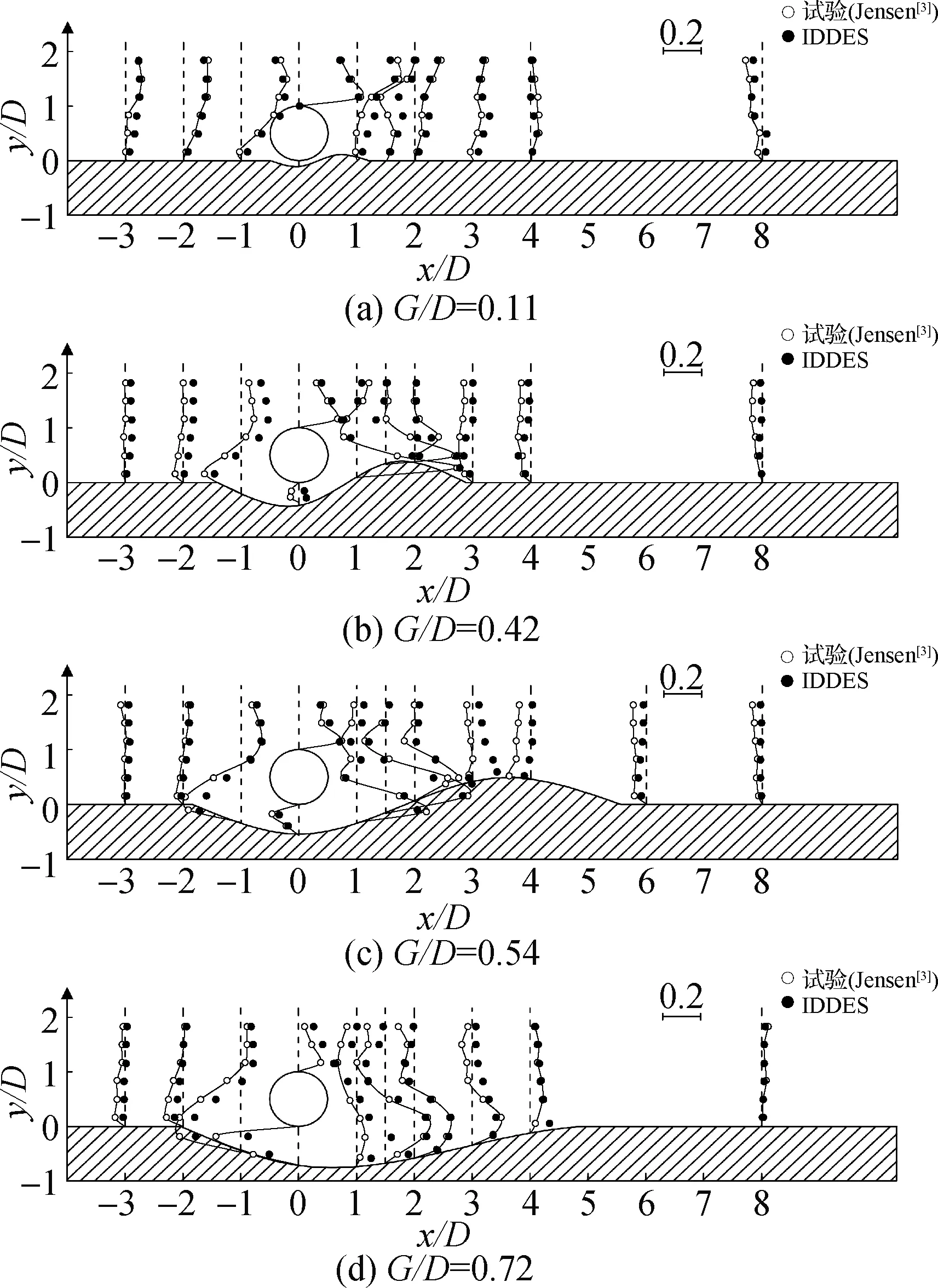
图4 时均垂直流速对比(z/D=2)

图5给出了采用IDDES模型与Smith等[4]采用LES模型和k-ε模型计算得到的时均水平速度均方根误差对比。在所有算例中，对于圆柱上游(-3≤x/D≤-1)入流边界层的预测，IDDES模拟结果略显优势，平均均方根误差仅为6.2%，而Smith等[4]在模拟中采用对数方法设定入流边界层，基于k-ε模型及LES模型4个算例的总平均均方根误差分别为14.2%及12.3%。对于圆柱尾流区域(0≤x/D≤4)预测，IDDES模型优势愈发明显，该模型对于这一区域预测误差稍有增加，总平均均方根误差为10.5%。而k-ε模型以及LES模型对于该区域预测误差大幅度提高，总平均均方根误差分别为30.0%及21.8%。分析表明采用IDDES模型对于水平流速模拟结果明显优于LES模型及k-ε模型。

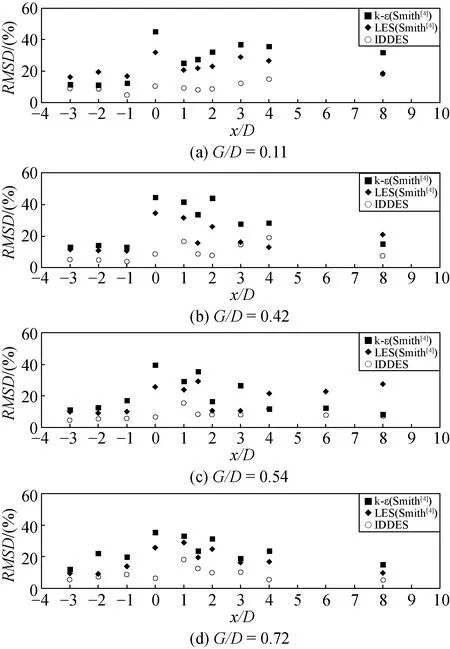
图5 时均水平速度均方根误差(z/D=2)

图6为三者模拟得到的时均垂直速度均方根误差对比。由于垂直流速较小，均方根误差值远低于时均水平速度均方根误差值。分析表明，在G/D=0.42及G/D=0.54的算例中，对于近尾流区域(1≤x/D≤1.5)，IDDES模型预测误差虽略有提高但并没有出现大幅波动，两个算例总平均均方根误差为4.2%，而k-ε模型以及LES模型预测误差出现跳跃式上升，总平均均方根误差分别为18.7%及16.3%。这可能是由于此时圆柱后方冲刷床出现了坡度较陡的沙坡，使得k-ε模型以及LES模型过度高估了沙坡影响。在其他位置，三者预测结果接近一致。

图6 时均垂直速度均方根误差(z/D=2)

Smith等[4]计算采用的两种方法中，雷诺平均方法由于受到边界条件、湍流模型条件等影响，其计算结果出现波动性可能较大，对流速预测误差相对较大；大涡模拟结果优于雷诺方法，但该方法计算三维模型时可靠度最高，计算量也十分庞大，对二维模型的计算仍有欠缺。通过前述分析可以发现IDDES模型弥补了上述两种方法的不足，计算得到的流速分布与试验结果吻合度更高，这进一步验证了该方法的可靠性。

3.2 时均流场分析

将各算例流场的水平流速进行时间平均，汇总如图7所示。整体来说，尾流场呈现出一定结构性，体现最为明显的便是圆柱底部的间隙流及圆柱下游回流区，其中间隙流流速受冲刷坑深度影响较大，而回流区范围与圆柱顶端和底端剪切层及间隙流有关。在G/D=0.11的情况下，圆柱尾流区约10D区域为回流区，该区域中心位置回流流速较大。这种现象的出现可能是由于冲刷坑并未完全发展，深度较浅，从冲刷坑绕过圆柱的水流虽然流速较大，但截面太小，流量仍然有限，大部分流体都是从圆柱上方绕过，此时间隙流强度较弱，因此流体从圆柱上方流过圆柱后产生大范围回流以补偿。而在G/D=0.42的情况下，由于冲刷坑已经发展至一定深度，间隙流强度及范围变大，圆柱底部出现剪切层，回流区域大幅缩减至1.3D范围。且由于沙坡的影响，间隙流及回流区均向上偏斜。在G/D=0.54的算例中，随着冲刷坑发展以及沙坡向后推移，回流区域又逐渐变大至1.7D，间隙流及回流区向上偏移程度减小。在G/D=0.72时，回流范围扩展至圆柱后方2D处，且回流区域流场逐渐关于圆柱中心所在水平线(y/D=0.5)对称。

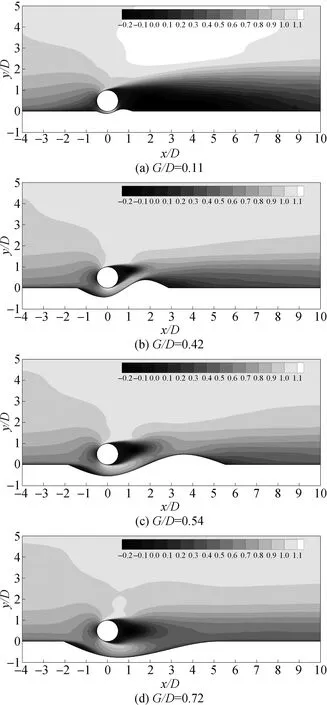
图7 时均水平流速(z/D=2)

图8给出了模拟得到的时均垂直流场。可以看到对于圆柱上游，4个算例来流方向几乎都是水平的，直到流动靠近圆柱时发生分离，形成上升流及下降流。而随着冲坑的逐渐发展，圆柱前方上升流区域逐渐缩小，而下降流区域逐渐扩大。在圆柱近尾流区均存在上升流，G/D=0.11的情况下由于后方出现的沙坡尺寸较小，上升流范围很小，但较浅的冲坑致使该区域流速较大。G/D=0.42时，由于冲坑后方沙坡已充分发展至较大尺寸且坡度陡峭，上升流范围较G/D=0.11的情况明显增大，二者最大流速相近。在G/D=0.54及G/D=0.72的算例中，随着沙坡向后推移以及坡度逐渐趋于平缓，上升流区域逐渐缩小，且流速逐渐降低。

图8 时均垂直流速(z/D=2)

3.3 瞬态流场涡量分析

涡识别技术目前已应用于各个领域，文中采用基于涡量的涡识别方法对圆柱下游涡街情况进行初步分析。在不同工况条件下，取圆柱跨中位置(z=2D)处截面作瞬态涡量图，如图9。在G/D=0.11的情况下，由于冲刷坑尚未发展至足够深度，壁面边界层对圆柱下游流场影响较大，且从间隙流过的流量有限，间隙流强度较弱。此时圆柱下游近壁面处出现4D长度范围的低涡量区，且并没有出现规则的涡脱落现象，仅圆柱顶部出现剪切层脱落，剪切层以小角度向上偏斜后，逐渐出现轻微的波动并向壁面靠近。在G/D=0.42的算例中，间隙流强度增大，圆柱顶部及底部均出现剪切层，底部剪切层在圆柱下游形成了回旋区域，并受到后方沙坡影响向上偏斜与圆柱顶部剪切层接触融合，有形成涡脱的趋势。在G/D=0.54的情况下，由于冲刷坑发展且沙坡向后方推移后坡度减缓，壁面边界层对圆柱底部间隙流影响逐渐减小。此时圆柱下游出现非对称的双排尾涡，底端逆时针涡由于壁面边界层及顶部剪切层的挤压而受到明显抑制，尺度小于顶端顺时针涡，并最终被抵消至下游仅存单侧泄涡。由于沙坡的存在，泄涡向上方偏离，通过沙坡后近乎平行于壁面向下游运动并在圆柱下游8D左右耗散。在G/D=0.72的情况下，由于冲刷坑已经完全展开，壁面边界层对圆柱底端间隙流影响进一步减小，此时圆柱顶部及底部剪切层在末段逐渐回旋、内扣，圆柱下游出现了稳定且几乎对称的双排涡街，尺度较G/D=0.54条件下的泄涡明显增大，并大致平行于壁面向下游移动，范围逐渐扩大。由于此时圆柱后方沙坡已经消失，因此涡脱耗散距离延长至圆柱下游10D左右。